写在前面
【三年面试五年模拟】栏目专注于分享AI行业中实习/校招/社招维度的必备面积知识点与面试方法,并向着更实战,更真实,更从容的方向不断优化迭代。也欢迎大家提出宝贵的意见或优化ideas,一起交流学习💪
大家好,我是Rocky。
本文是“三年面试五年模拟”之独孤九剑秘籍的特别系列,Rocky将独孤九剑秘籍前十二式的内容进行汇总梳理成汇总篇,并制作成pdf版本
由于【三年面试五年模拟】系列都是Rocky在工作之余进行整理总结,难免有疏漏与错误之处,欢迎大家对可优化的部分进行指正,我将在后续的优化迭代版本中及时更正。
在【人人都是算法工程师】算法工程师的“三年面试五年模拟”之独孤九剑秘籍(先行版)中我们阐述了这个program的愿景与规划。本系列接下来的每一篇文章都将以独孤九剑秘籍框架的逻辑展开,考虑到易读性与文章篇幅,一篇文章中只选取每个分支技能树中的2-3个经典&高价值知识点和面试问题,并配以相应的参考答案(精简版),供大家参考。
希望独孤九剑秘籍的每一式都能让江湖中的英雄豪杰获益。

So,enjoy(与本文的BGM一起食用更佳哦):
正文开始
----【目录先行】----
深度学习基础:
-
什么是转置卷积的棋盘效应?
-
Instance Normalization的作用?
-
什么是有效感受野?
-
全局池化的作用?
-
深度学习中有哪些经典的优化器?
-
有哪些提高GAN训练稳定性的Tricks?
-
深度学习炼丹可以调节的一些超参数?
-
滑动平均的相关概念
-
Spectral Normalization的相关知识
-
激活函数的作用,常用的激活函数有哪些?
-
反向传播算法(BP)的概念及简单推导
-
分组卷积的相关知识
经典模型&&热门模型:
-
Focal Loss的作用?
-
YOLO系列的面试问题
-
有哪些经典的轻量型人脸检测模型?
-
LFFD人脸检测模型的结构和特点?
-
U-Net模型的结构和特点?
-
RepVGG模型的结构和特点?
-
GAN的核心思想?
-
面试常问的经典GAN模型?
-
FPN(Feature Pyramid Network)的相关知识
-
SPP(Spatial Pyramid Pooling)的相关知识
-
目标检测中AP,AP50,AP75,mAP等指标的含义
-
YOLOv2中的anchor如何生成?
机器学习基础:
-
机器学习有哪些种类?
-
L1正则为什么比L2正则更容易产生稀疏解?
-
格拉姆矩阵的相关概念?
-
感知损失的相关概念?
-
Accuracy、Precision、Recall、F1 Scores的相关概念?
-
梯度爆炸和梯度消失产生的原因及解决方法?
-
数据EDA逻辑(Exploratory Data Analysis)?
-
K折交叉验证逻辑?
-
KL散度相关概念
-
JS散度相关概念
-
K-means算法逻辑?
-
K近邻算法逻辑?
Python/C/C++知识:
-
Python中assert的作用?
-
Python中互换变量有不用创建临时变量的方法吗?
-
Python中的主要数据结构都有哪些?
-
Python中的可变对象和不可变对象?
-
Python中的None代表什么?
-
Python中 ∗ a r g s *args ∗args和 ∗ ∗ k w a r g s **kwargs ∗∗kwargs的区别?
-
Python中Numpy的broadcasting机制?
-
Python中的实例方法、静态方法和类方法三者区别?
-
Python中常见的切片操作
-
Python中如何进行异常处理?
-
Python中remove,del以及pop之间的区别?
-
C/C++中内存泄漏以及解决方法?
-
C/C++中野指针的概念?
-
C/C++中面向对象和面向过程的区别?
-
C/C++中常用容器功能汇总
-
C/C++中指针和引用的区别
-
C/C++中宏定义的相关知识
-
C/C++中typedef关键字的相关知识
模型部署:
-
什么是异构计算?
-
端侧部署时整个解决方案的核心指标?
-
什么是模型量化?
-
什么是模型剪枝?
-
主流AI端侧硬件平台有哪些?
-
主流AI端侧硬件平台一般包含哪些模块?
-
算法工程师该如何看待硬件侧知识?
-
现有的一些移动端开源框架?
-
端侧静态多Batch和动态多Batch的区别?
-
优化模型端侧性能的一些方法
-
ONNX的相关知识
-
TensorRT的相关知识
图像处理基础:
-
有哪些常用的图像质量评价指标?
-
什么是图像畸变?
-
RGB图像转为灰度图的方法?
-
仿射变换和透视变换的概念?
-
图像噪声的种类?
-
Python中OpenCV和PIL的区别?
-
有哪些常用的图像去噪算法?
-
有哪些常用的图像频域信息分离方法?
-
有哪些常用一阶微分梯度算子?
-
拉普拉斯算子的相关概念
-
OpenCV读取图像的格式?
-
中值滤波与均值滤波的相关概念
计算机基础:
-
Linux中的进程状态种类
-
Linux中ps aux指令与grep指令配合管理进程
-
Git,GitLab,SVN的相关知识
-
协程的相关概念
-
Linux系统的相关概念
-
Linux系统和Windows系统的区别?
-
POC验证测试的概念
-
Docker的相关概念及常用命令
-
深度学习中常用的文件格式汇总
-
TCP和UDP的区别?
开放性问题:
-
不同性质的公司如何使用好AI技术?
-
新时期的AI Lab该如何搭建?
-
业务侧,竞赛侧,研究侧成果如何互相转化?
-
深度学习的优势和局限?
-
如何保持数据持续稳定的支持业务?
-
如何分辨demo业务,一次性业务以及外包业务?
-
你觉得有哪些方法能增强公司的AI影响力?
-
你觉得面对一个业务场景,如何针对性设计算法解决方案?
-
对AI安全相关技术的发展前景的看法?
-
对GAN算法技术的发展前景的看法?
-
对一个零基础的CV算法学习者,有什么入门建议?
-
对CV算法技术的发展前景的看法?
----【深度学习基础】----
【一】什么是转置卷积的棋盘效应?

造成棋盘效应的原因是转置卷积的不均匀重叠(uneven overlap)。这种重叠会造成图像中某个部位的颜色比其他部位更深。
在下图展示了棋盘效应的形成过程,深色部分代表了不均匀重叠:
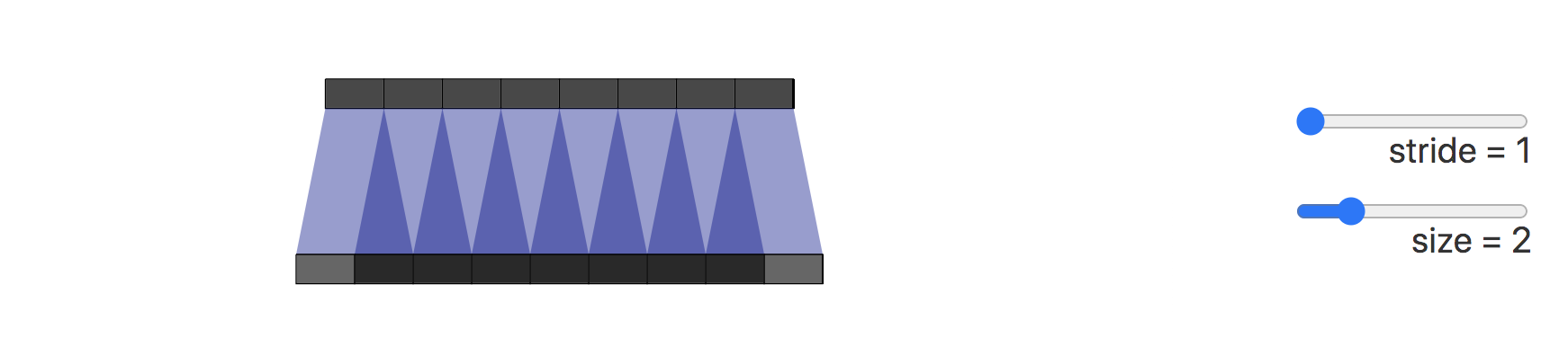
接下来我们将卷积步长改为2,可以看到输出图像上的所有像素从输入图像中接收到同样多的信息,它们都从输入图像中接收到一个像素的信息,这样就不存在转置卷带来的重叠区域。

我们也可以直接进行插值Resize操作,然后再进行卷积操作来消除棋盘效应。这种方式在超分辨率重建场景中比较常见。例如使用双线性插值和近邻插值等方法来进行上采样。
【二】Instance Normalization的作用?
Instance Normalization(IN)和Batch Normalization(BN)一样,也是Normalization的一种方法,只是IN是作用于单张图片,而BN作用于一个Batch。
BN对Batch中的每一张图片的同一个通道一起进行Normalization操作,而IN是指单张图片的单个通道单独进行Normalization操作。如下图所示,其中C代表通道数,N代表图片数量(Batch)。
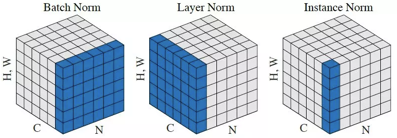
IN适用于生成模型中,比如图片风格迁移。因为图片生成的结果主要依赖于某个图像实例,所以对整个Batch进行Normalization操作并不适合图像风格化的任务,在风格迁移中使用IN不仅可以加速模型收敛,并且可以保持每个图像实例之间的独立性。
下面是IN的公式:
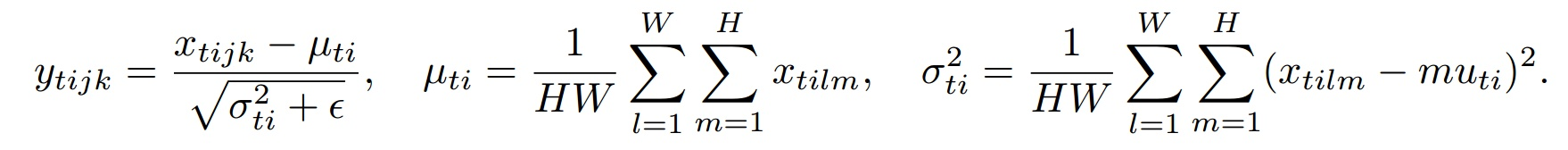
其中t代表图片的index,i代表的是feature map的index。
【三】什么是有效感受野?
感受野的相关知识在之前的文章【三年面试五年模拟】算法工程师的独孤九剑秘籍(前六式汇总篇)中介绍过。
我们接着再看看有效感受野(effective receptive field, ERF)的相关知识。
一般而言,feature map上有效感受野要小于实际感受野。其有效性,以中心点为基准,类似高斯分布向边缘递减。
总的来说,感受野主要描述feature map中的最大信息量,有效感受野则主要描述信息的有效性。
【四】全局池化的作用?
全局池化主要包括全局平均池化和全局最大池化。
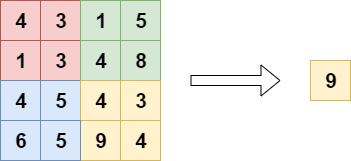
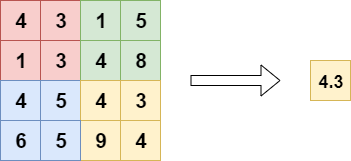
接下来,Rocky以全局平均池化为例,讲述其如何在深度学习网络中发挥作用。
刚才已经讲过,全局平均池化就是对最后一层卷积的特征图,每个通道求整个特征图的均值。如下图所示:
一般网络的最后会再接几个全连接层,但全局池化后的feature map相当于一像素,所以最后的全连接其实就成了一个加权相加的操作。这种结构比起直接的全连接更加直观,参数量大大幅下降,并且泛化性能更好:

全局池化的作用:
- 代替全连接层,降低参数量。
- 减少过拟合,增加泛化能力。
【五】深度学习中有哪些经典的优化器?
SGD(随机梯度下降)
随机梯度下降的优化算法在科研和工业界是很常用的。
很多理论和工程问题都能转化成对目标函数进行最小化的数学问题。
举个例子:梯度下降(Gradient Descent)就好比一个人想从高山上奔跑到山谷最低点,用最快的方式奔向最低的位置。
SGD的公式:

动量(Momentum)公式:

基本的mini-batch SGD优化算法在深度学习取得很多不错的成绩。然而也存在一些问题需解决:
- 选择恰当的初始学习率很困难。
- 学习率调整策略受限于预先指定的调整规则。
- 相同的学习率被应用于各个参数。
- 高度非凸的误差函数的优化过程,如何避免陷入大量的局部次优解或鞍点。
AdaGrad(自适应梯度)
AdaGrad优化算法(Adaptive Gradient,自适应梯度),它能够对每个不同的参数调整不同的学习率,对频繁变化的参数以更小的步长进行更新,而稀疏的参数以更大的步长进行更新。
AdaGrad公式:


g t , i g_{t,i} gt,i表示t时刻的 θ i \theta_{i} θi梯度。
G t , i i G_{t,ii} Gt,ii表示t时刻参数 θ i \theta_{i} θi的梯度平方和。
与SGD的核心区别在于计算更新步长时,增加了分母:梯度平方累积和的平方根。此项能够累积各个参数 θ i \theta_{i} θi的历史梯度平方,频繁更新的梯度,则累积的分母逐渐偏大,那么更新的步长相对就会变小,而稀疏的梯度,则导致累积的分母项中对应值比较小,那么更新的步长则相对比较大。
AdaGrad能够自动为不同参数适应不同的学习率(平方根的分母项相当于对学习率α进进行了自动调整,然后再乘以本次梯度),大多数的框架实现采用默认学习率α=0.01即可完成比较好的收敛。
优势: 在数据分布稀疏的场景,能更好利用稀疏梯度的信息,比标准的SGD算法更有效地收敛。
缺点: 主要缺陷来自分母项的对梯度平方不断累积,随时间的增加,分母项越来越大,最终导致学习率收缩到太小无法进行有效更新。
RMSProp
RMSProp结合梯度平方的指数移动平均数来调节学习率的变化。能够在不稳定的目标函数情况下进行很好地收敛。
计算t时刻的梯度:

计算梯度平方的指数移动平均数(Exponential Moving Average), γ \gamma γ是遗忘因子(或称为指数衰减率),依据经验,默认设置为0.9。

梯度更新的时候,与AdaGrad类似,只是更新的梯度平方的期望(指数移动均值),其中 ε = 1 0 − 8 \varepsilon = 10^{-8} ε=10−8,避免除数为0。默认学习率 α = 0.001 \alpha = 0.001 α=0.001。

优势: 能够克服AdaGrad梯度急剧减小的问题,在很多应用中都展示出优秀的学习率自适应能力。尤其在不稳定(Non-Stationary)的目标函数下,比基本的SGD、Momentum、AdaGrad表现更良好。
Adam
Adam优化器结合了AdaGrad和RMSProp两种优化算法的优点。对梯度的一阶矩估计(First Moment Estimation,即梯度的均值)和二阶矩估计(Second Moment Estimation,即梯度的未中心化的方差)进行综合考虑,计算出更新步长。
Adam的优势:
- 实现简单,计算高效,对内存需求少。
- 参数的更新不受梯度的伸缩变换影响。
- 超参数具有很好的解释性,且通常无需调整或仅需很少的微调。
- 更新的步长能够被限制在大致的范围内(初始学习率)。
- 能自然地实现步长退火过程(自动调整学习率)。
- 很适合应用于大规模的数据及参数的场景。
- 适用于不稳定目标函数。
- 适用于梯度稀疏或梯度存在很大噪声的问题。
Adam的实现原理:

计算t时刻的梯度:

然后计算梯度的指数移动平均数, m 0 m_{0} m0初始化为0。
类似于Momentum算法,综合考虑之前累积的梯度动量。
β 1 \beta_{1} β1系数为指数衰减率,控制动量和当前梯度的权重分配,通常取接近于1的值。默认为0.9。

接着,计算梯度平方的指数移动平均数, v 0 v_{0} v0初始化为0。
β 2 \beta_{2} β2系数为指数衰减率,控制之前的梯度平方的影响情况。默认为0.999。
类似于RMSProp算法,对梯度平方进行加权均值。

由于 m 0 m_{0} m0初始化为0,会导致 m t m_{t} mt偏向于0,尤其在训练初期阶段。
所以,此处需要对梯度均值 m t m_{t} mt进行偏差纠正,降低偏差对训练初期的影响。

同时 v 0 v_{0} v0也要进行偏差纠正:

最后总的公式如下所示:

其中默认学习率 α = 0.001 \alpha = 0.001 α=0.001, ε = 1 0 − 8 \varepsilon = 10^{-8} ε=10−8避免除数变为0。
从表达式中可以看出,对更新的步长计算,能够从梯度均值和梯度平方两个角度进行自适应地调节,而不是直接由当前梯度决定。
Adam的不足:
虽然Adam算法目前成为主流的优化算法,不过在很多领域里(如计算机视觉的图像识别、NLP中的机器翻译)的最佳成果仍然是使用带动量(Momentum)的SGD来获取到的。
【六】有哪些提高GAN训练稳定性的Tricks?
1.输入Normalize
- 将输入图片Normalize到 [ − 1 , 1 ] [-1,1] [−1,1]之间。
- 生成器最后一层的输出使用Tanh激活函数。
Normalize非常重要,没有处理过的图片是没办法收敛的。图片Normalize一种简单的方法是(images-127.5)/127.5,然后送到判别器去训练。同理生成的图片也要经过判别器,即生成器的输出也是-1到1之间,所以使用Tanh激活函数更加合适。
2.替换原始的GAN损失函数和标签反转
-
原始GAN损失函数会出现训练早期梯度消失和Mode collapse(模型崩溃)问题。可以使用Earth Mover distance(推土机距离)来优化。
-
实际工程中用反转标签来训练生成器更加方便,即把生成的图片当成real的标签来训练,把真实的图片当成fake来训练。
3.使用具有球形结构的随机噪声 Z Z Z作为输入
- 不要使用均匀分布进行采样

- 使用高斯分布进行采样
4.使用BatchNorm
- 一个mini-batch中必须只有real数据或者fake数据,不要把他们混在一起训练。
- 如果能用BatchNorm就用BatchNorm,如果不能用则用instance normalization。

5.避免使用ReLU,MaxPool等操作引入稀疏梯度
- GAN的稳定性会因为引入稀疏梯度受到很大影响。
- 最好使用类LeakyReLU的激活函数。(D和G中都使用)
- 对于下采样,最好使用:Average Pooling或者卷积+stride。
- 对于上采样,最好使用:PixelShuffle或者转置卷积+stride。
最好去掉整个Pooling逻辑,因为使用Pooling会损失信息,这对于GAN训练没有益处。
6.使用Soft和Noisy的标签
- Soft Label,即使用 [ 0.7 − 1.2 ] [0.7-1.2] [0.7−1.2]和 [ 0 − 0.3 ] [0-0.3] [0−0.3]两个区间的随机值来代替正样本和负样本的Hard Label。
- 可以在训练时对标签加一些噪声,比如随机翻转部分样本的标签。
7.使用Adam优化器
- Adam优化器对于GAN来说非常有用。
- 在生成器中使用Adam,在判别器中使用SGD。
8.追踪训练失败的信号
- 判别器的损失=0说明模型训练失败。
- 如果生成器的损失稳步下降,说明判别器没有起作用。
9.在输入端适当添加噪声
- 在判别器的输入中加入一些人工噪声。
- 在生成器的每层中都加入高斯噪声。
10.生成器和判别器差异化训练
- 多训练判别器,尤其是加了噪声的时候。
11.Two Timescale Update Rule (TTUR)
对判别器和生成器使用不同的学习速度。使用较低的学习率更新生成器,判别器使用较高的学习率进行更新。
12. Gradient Penalty (梯度惩罚)
使用梯度惩罚机制可以极大增强 GAN 的稳定性,尽可能减少mode collapse问题的产生。
13. Spectral Normalization(谱归一化)
Spectral normalization可以用在判别器的weight normalization技术,可以确保判别器是K-Lipschitz连续的。
14. 使用多个GAN结构
可以使用多个GAN/多生成器/多判别器结构来让GAN训练更稳定,提升整体效果,解决更难的问题。
【七】深度学习炼丹可以调节的一些超参数?
- 预处理(数据尺寸,数据Normalization)
- Batch-Size
- 学习率
- 优化器
- 损失函数
- 激活函数
- Epoch
- 权重初始化
- NAS网络架构搜索
【八】滑动平均的相关概念
滑动平均(exponential moving average),或者叫做指数加权平均(exponentially weighted moving avergae),可以用来估计变量的局部均值,使得变量的更新与一段时间内的历史取值有关。
变量 v v v在 t t t时刻记为 v t v_{t} vt, θ t \theta_{t} θt为变量 v v v在 t t t时刻训练后的取值,当不使用滑动平均模型时 v t = θ t v_{t} = \theta_{t} vt=θt,在使用滑动平均模型后, v t v_{t} vt的更新公式如下:

上式中, β ϵ [ 0 , 1 ) \beta\epsilon[0,1) βϵ[0,1)。 β = 0 \beta = 0 β=0相当于没有使用滑动平均。
t t t时刻变量 v v v的滑动平均值大致等于过去 1 / ( 1 − β ) 1/(1-\beta) 1/(1−β)个时刻 θ \theta θ值的平均。并使用bias correction将 v t v_{t} vt除以 ( 1 − β t ) (1 - \beta^{t}) (1−βt)修正对均值的估计。
加入Bias correction后, v t v_{t} vt和 v b i a s e d t v_{biased_{t}} vbiasedt的更新公式如下:

当 t t t越大, 1 − β t 1 - \beta^{t} 1−βt越接近1,则公式(1)和(2)得到的结果( v t v_{t} vt和 v b i a s e d 1 v_{biased_{1}} vbiased1)将越来越接近。
当 β \beta β越大时,滑动平均得到的值越和 θ \theta θ的历史值相关。如果 β = 0.9 \beta = 0.9 β=0.9,则大致等于过去10个 θ \theta θ值的平均;如果 β = 0.99 \beta = 0.99 β=0.99,则大致等于过去100个 θ \theta θ值的平均。
下图代表不同方式计算权重的结果:
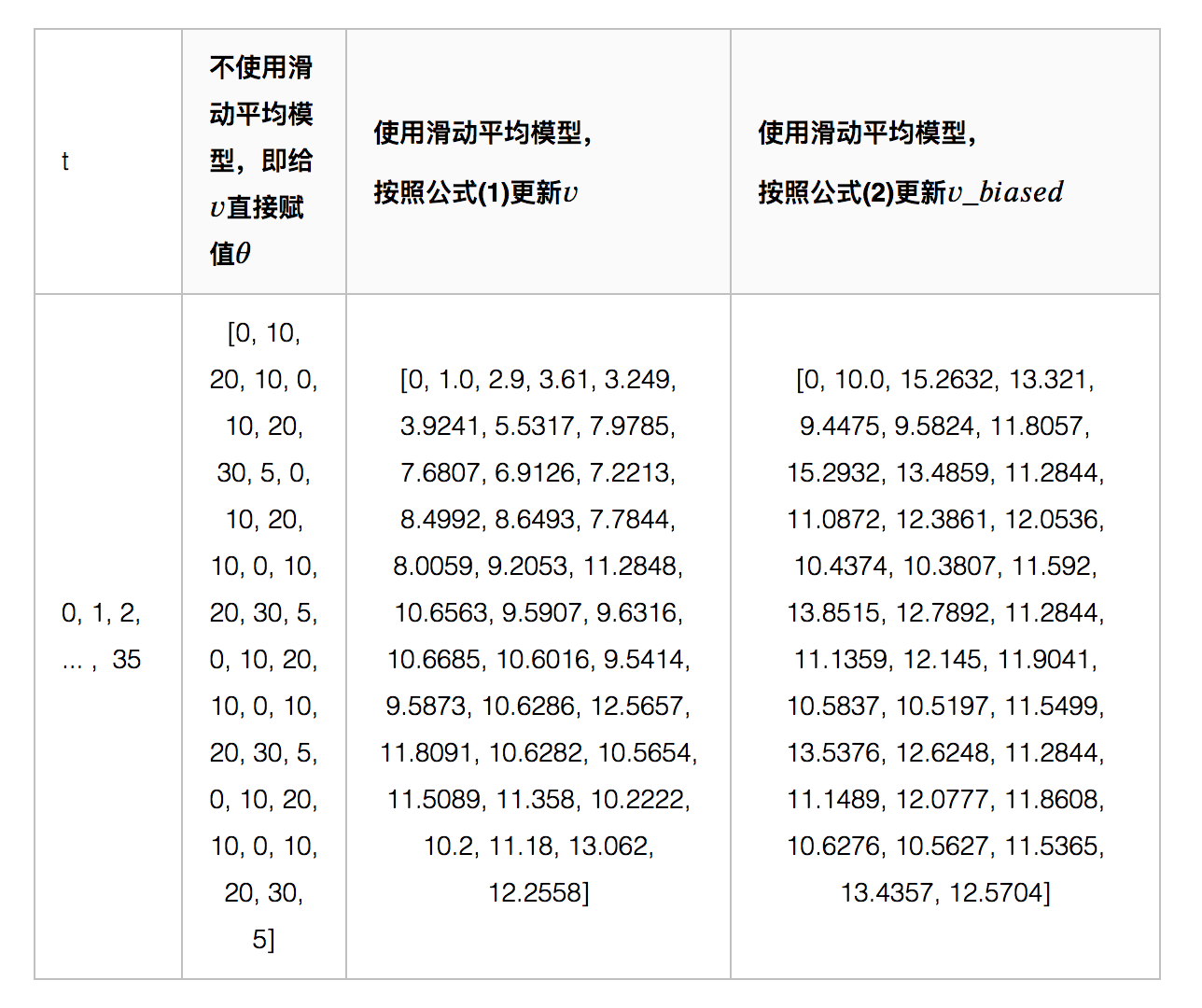
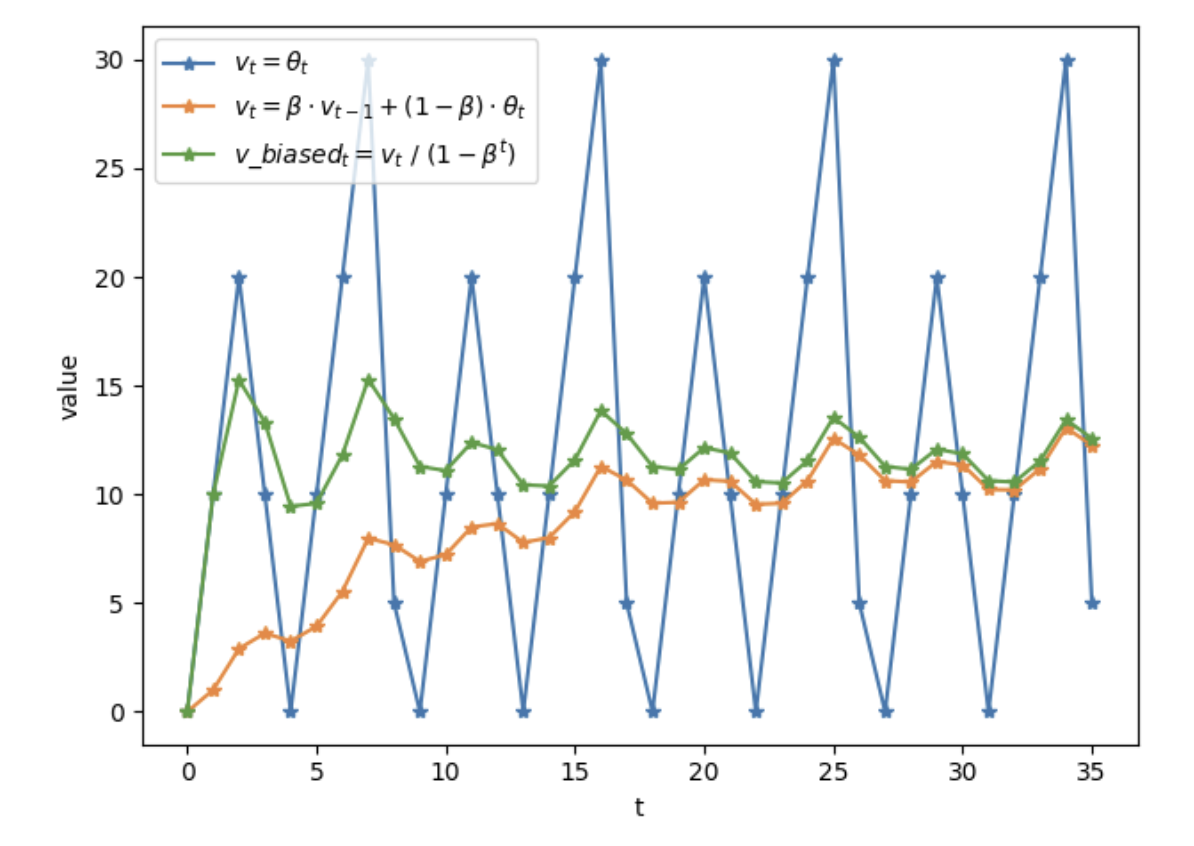
如上图所示,滑动平均可以看作是变量的过去一段时间取值的均值,相比对变量直接赋值而言,滑动平均得到的值在图像上更加平缓光滑,抖动性更小,不会因为某种次的异常取值而使得滑动平均值波动很大。
滑动平均的优势: 占用内存少,不需要保存过去10个或者100个历史 θ \theta θ值,就能够估计其均值。滑动平均虽然不如将历史值全保存下来计算均值准确,但后者占用更多内存,并且计算成本更高。
为什么滑动平均在测试过程中被使用?
滑动平均可以使模型在测试数据上更鲁棒(robust)。
采用随机梯度下降算法训练神经网络时,使用滑动平均在很多应用中都可以在一定程度上提高最终模型在测试数据上的表现。
训练中对神经网络的权重 w e i g h t s weights weights 使用滑动平均,之后在测试过程中使用滑动平均后的 w e i g h t s weights weights 作为测试时的权重,这样在测试数据上效果更好。因为滑动平均后的 w e i g h t s weights weights 的更新更加平滑,对于随机梯度下降而言,更平滑的更新说明不会偏离最优点很远。比如假设decay=0.999,一个更直观的理解,在最后的1000次训练过程中,模型早已经训练完成,正处于抖动阶段,而滑动平均相当于将最后的1000次抖动进行了平均,这样得到的权重会更加鲁棒。
【九】Spectral Normalization的相关知识
Spectral Normalization是一种wegiht Normalization技术,和weight-clipping以及gradient penalty一样,也是让模型满足1-Lipschitz条件的方式之一。
Lipschitz(利普希茨)条件限制了函数变化的剧烈程度,即函数的梯度,来确保统计的有界性。因此函数更加平滑,在神经网络的优化过程中,参数变化也会更稳定,不容易出现梯度爆炸。
Lipschitz条件的约束如下所示:
∣ ∣ f ( x ) − f ( x ′ ) ∣ ∣ 2 ∣ ∣ x − x ′ ∣ ∣ 2 ⩽ K \frac{||f(x) -f(x^\prime)||_{2}}{||x - x^\prime||_{2}} \leqslant K ∣∣x−x′∣∣2∣∣f(x)−f(x′)∣∣2⩽K
其中 K K K代表一个常数,即利普希茨常数。若 K = 1 K=1 K=1,则是1-Lipschitz。
在GAN领域,Spectral Normalization有很多应用。在WGAN中,只有满足1-Lipschitz约束时,W距离才能转换成较好求解的对偶问题,使得WGAN更加从容的训练。
如果想让矩阵A映射: R n → R m R^{n}\to R^{m} Rn→Rm满足K-Lipschitz连续,K的最小值为 λ 1 \sqrt{\lambda_{1}} λ1( λ 1 \lambda_{1} λ1是 A T A A_TA ATA的最大特征值),那么要想让矩阵A满足1-Lipschitz连续,只需要在A的所有元素上同时除以 λ 1 \sqrt{\lambda_{1}} λ1(Spectral norm)。
Spectral Normalization实际上在做的事,是将每层的参数矩阵除以自身的最大奇异值,本质上是一个逐层SVD的过程,但是真的去做SVD就太耗时了,所以采用幂迭代的方法求解。过程如下图所示:

得到谱范数 σ l ( W ) \sigma_l(W) σl(W)后,每个参数矩阵上的参数皆除以它,以达到Normalization的目的。
【十】激活函数的作用,常用的激活函数有哪些?
激活函数的作用
激活函数可以引入非线性因素,提升网络的学习表达能力。
常用的激活函数
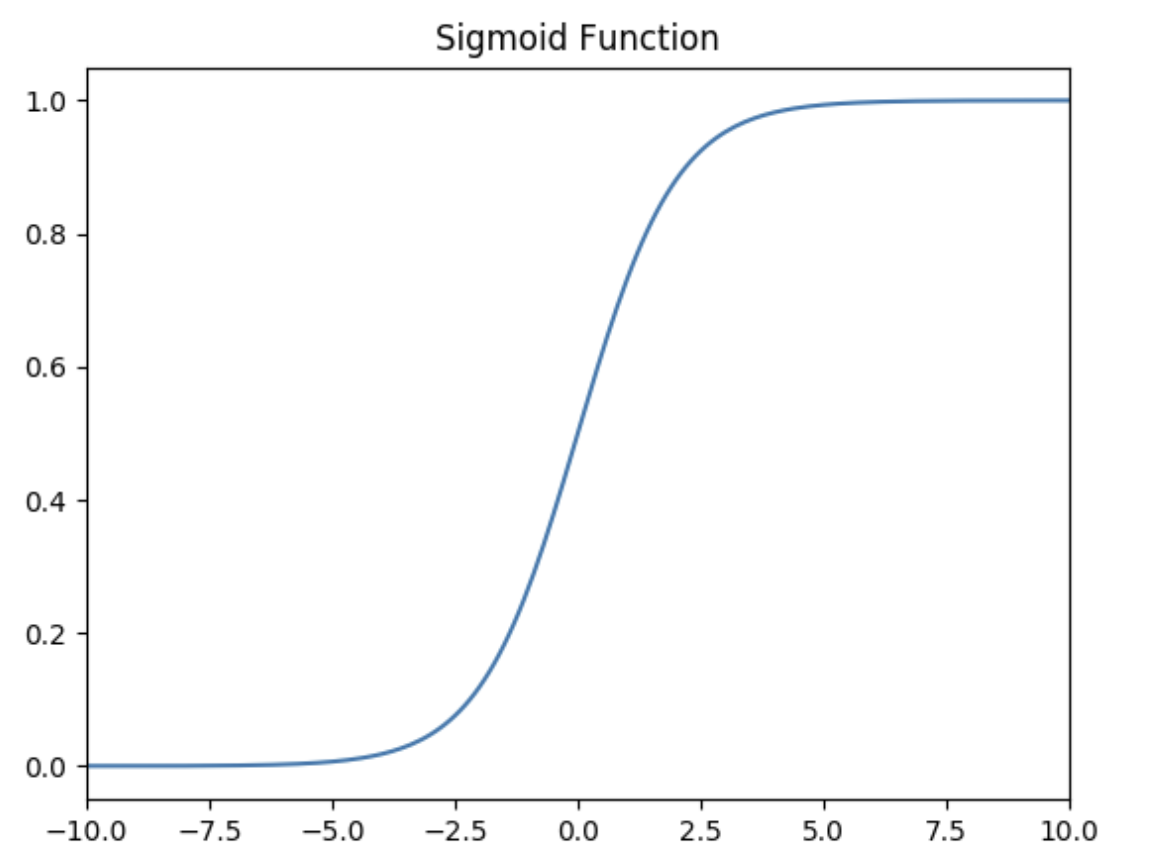
Sigmoid 激活函数
函数的定义为:
f ( x ) = 1 1 + e − x f(x) = \frac{1}{1 + e^{-x}} f(x)=1+e−x1
如下图所示,其值域为 ( 0 , 1 ) (0,1) (0,1)。也就是说,输入的每个神经元、节点都会被缩放到一个介于 0 0 0和 1 1 1之间的值。
当 x x x大于零时输出结果会趋近于 1 1 1,而当 x x x小于零时,输出结果趋向于 0 0 0,由于函数的特性,经常被用作二分类的输出端激活函数。
Sigmoid的导数:
f ′ ( x ) = ( 1 1 + e − x ) ′ = 1 1 + e − x ( 1 − 1 1 + e − x ) = f ( x ) ( 1 − f ( x ) ) f^{'}(x)=(\frac{1}{1+e^{-x}})^{'}=\frac{1}{1+e^{-x}}\left( 1- \frac{1}{1+e^{-x}} \right)=f(x)(1-f(x)) f′(x)=(1+e−x1)′=1+e−x1(1−1+e−x1)=f(x)(1−f(x))
当 x = 0 x=0 x=0时, f ( x ) ′ = 0.25 f(x)'=0.25 f(x)′=0.25。
Sigmoid的优点:
- 平滑
- 易于求导
- 可以作为概率,辅助解释模型的输出结果
Sigmoid的缺陷:
- 当输入数据很大或者很小时,函数的梯度几乎接近于0,这对神经网络在反向传播中的学习非常不利。
- Sigmoid函数的均值不是0,这使得神经网络的训练过程中只会产生全正或全负的反馈。
- 导数值恒小于1,反向传播易导致梯度消失。
Tanh激活函数
Tanh函数的定义为:
f ( x ) = T a n h ( x ) = e x − e − x e x + e − x f(x) = Tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} f(x)=Tanh(x)=ex+e−xex−e−x
如下图所示,值域为 ( − 1 , 1 ) (-1,1) (−1,1)。
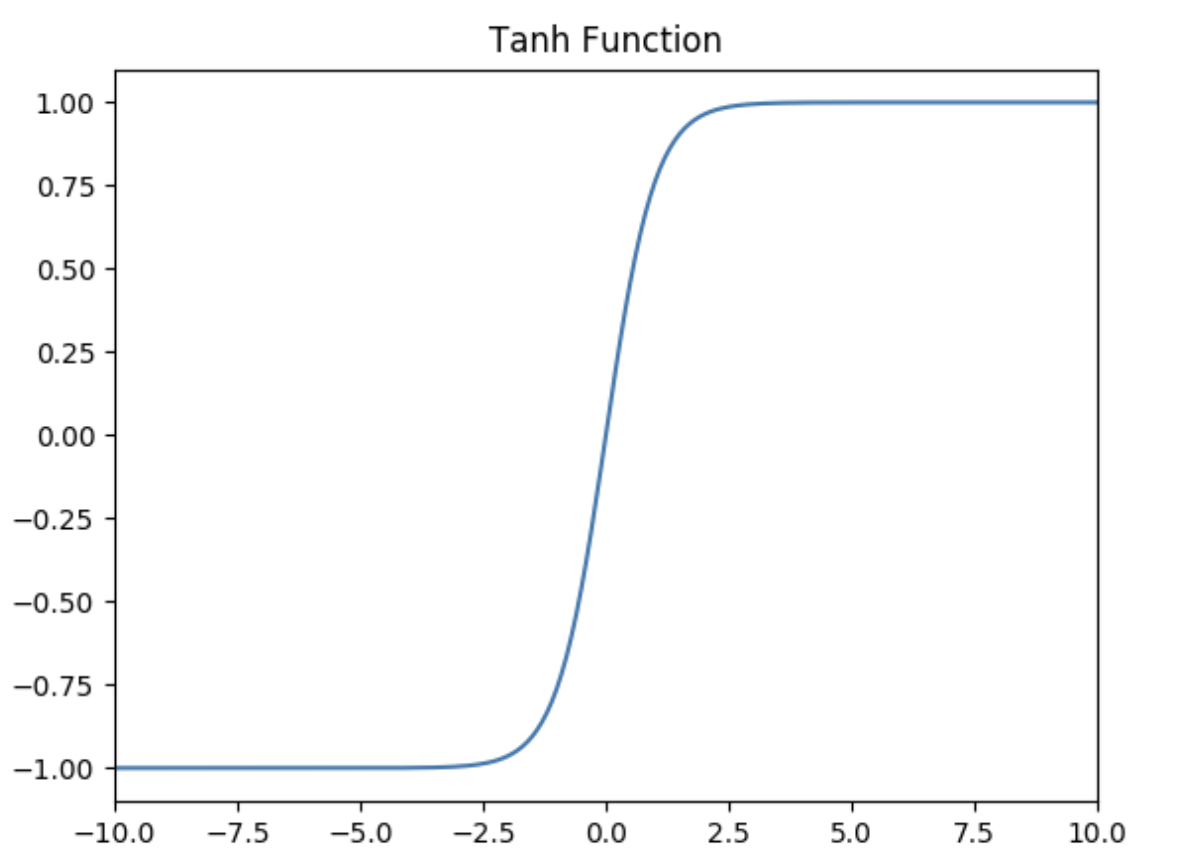
Tanh的优势:
- Tanh函数把数据压缩到-1到1的范围,解决了Sigmoid函数均值不为0的问题,所以在实践中通常Tanh函数比Sigmoid函数更容易收敛。在数学形式上其实Tanh只是对Sigmoid的一个缩放形式,公式为 t a n h ( x ) = 2 f ( 2 x ) − 1 tanh(x) = 2f(2x) -1 tanh(x)=2f(2x)−1( f ( x ) f(x) f(x)是Sigmoid的函数)。
- 平滑
- 易于求导
Tanh的导数:
f ′ ( x ) = ( e x − e − x e x + e − x ) ′ = 1 − ( t a n h ( x ) ) 2 f^{'}(x)=(\frac{e^x - e^{-x}}{e^x + e^{-x}})^{'}=1-(tanh(x))^2 f′(x)=(ex+e−xex−e−x)′=1−(tanh(x))2
当 x = 0 x=0 x=0时, f ( x ) ′ = 1 f(x)'=1 f(x)′=1。
由Tanh和Sigmoid的导数也可以看出Tanh导数更陡,收敛速度比Sigmoid快。
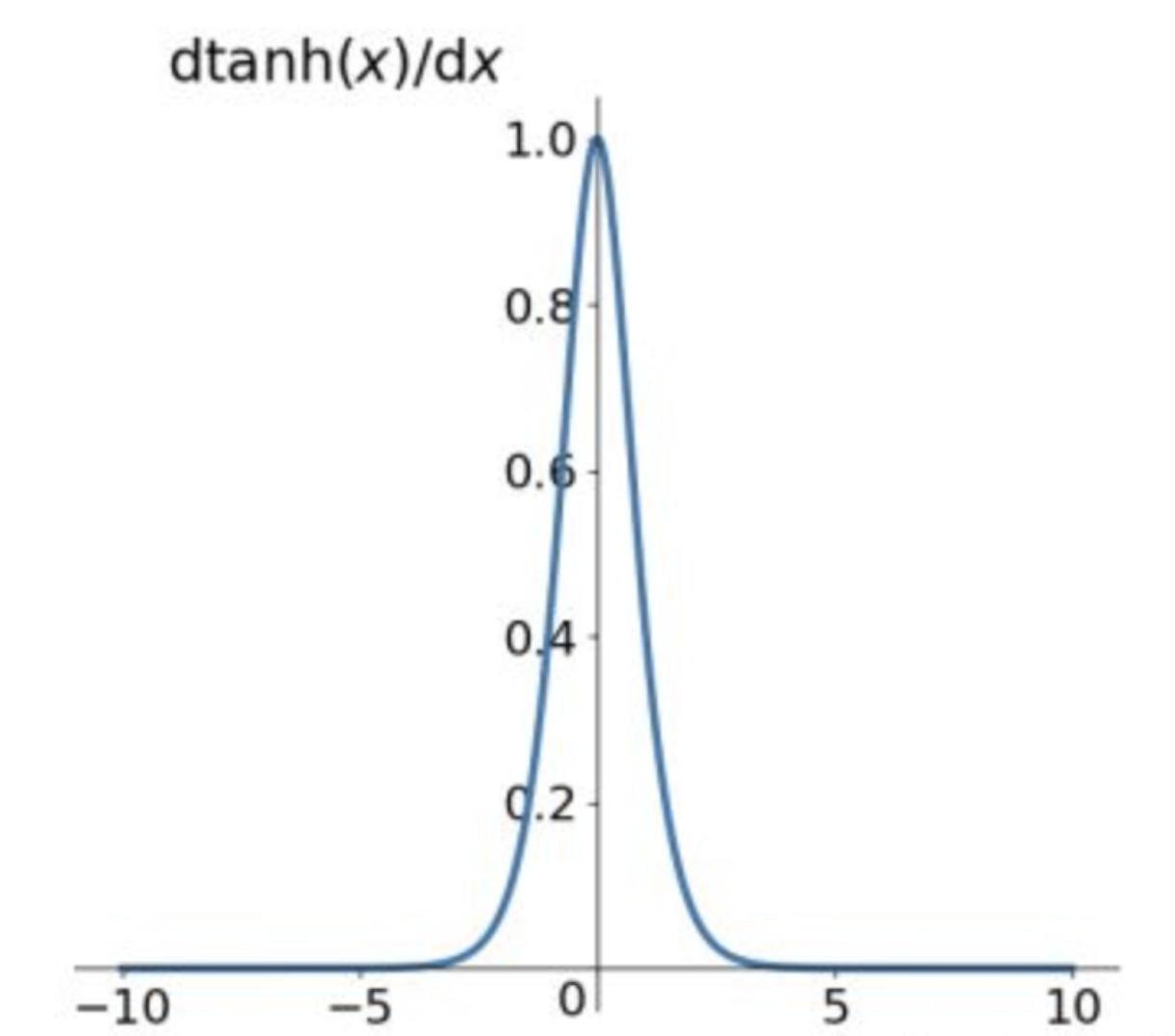
Tanh的缺点:
导数值恒小于1,反向传播易导致梯度消失。
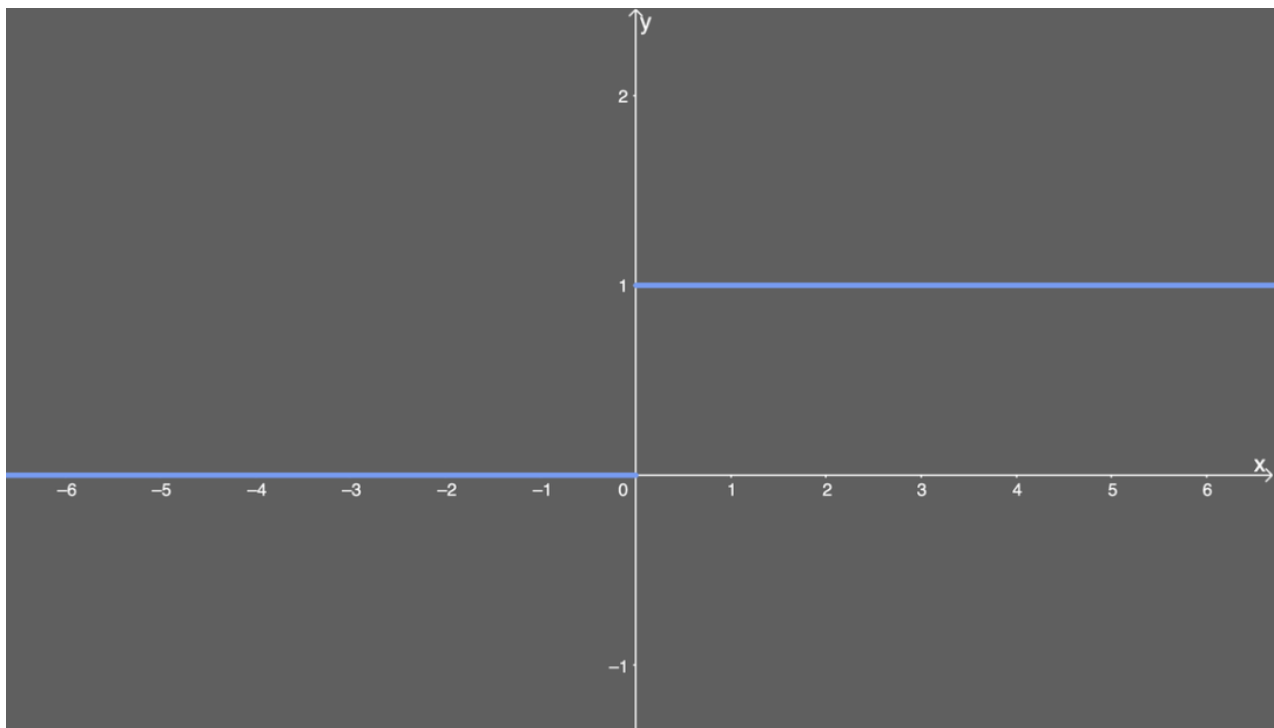
Relu激活函数
Relu激活函数的定义为:
f ( x ) = m a x ( 0 , x ) f(x) = max(0, x) f(x)=max(0,x)
如下图所示,值域为 [ 0 , + ∞ ) [0,+∞) [0,+∞)。

ReLU的优势:
- 计算公式非常简单,不像上面介绍的两个激活函数那样涉及成本更高的指数运算,大量节约了计算时间。
- 在随机梯度下降中比Sigmoid和Tanh更加容易使得网络收敛。
- ReLU进入负半区的时候,梯度为0,神经元此时会训练形成单侧抑制,产生稀疏性,能更好更快地提取稀疏特征。
- Sigmoid和Tanh激活函数的导数在正负饱和区的梯度都会接近于0,这会造成梯度消失,而ReLU函数大于0部分都为常数保持梯度不衰减,不会产生梯度消失现象。
稀疏:在神经网络中,这意味着激活的矩阵含有许多0。这种稀疏性能让我们得到什么?这能提升时间和空间复杂度方面的效率,常数值所需空间更少,计算成本也更低。
ReLU的导数:
c ( u ) = { 0 , x < 0 1 , x > 0 u n d e f i n e d , x = 0 c(u)=\begin{cases} 0,x<0 \\ 1,x>0 \\ undefined,x=0\end{cases} c(u)=⎩ ⎨ ⎧0,x<01,x>0undefined,x=0
通常 x = 0 x=0 x=0时,给定其导数为 1 1 1和 0 0 0。
ReLU的不足:
- 训练中可能会导致出现某些神经元永远无法更新的情况。其中一种对ReLU函数的改进方式是LeakyReLU。
- ReLU不能避免梯度爆炸问题。
LeakyReLU激活函数
LeakyReLU激活函数定义为:
f ( x ) = { a x , x < 0 x , x ≥ 0 f(x) = \left\{ \begin{aligned} ax, \quad x<0 \\ x, \quad x\ge0 \end{aligned} \right. f(x)={ax,x<0x,x≥0
如下图所示( a = 0.5 a = 0.5 a=0.5),值域为 ( − ∞ , + ∞ ) (-∞,+∞) (−∞,+∞)。
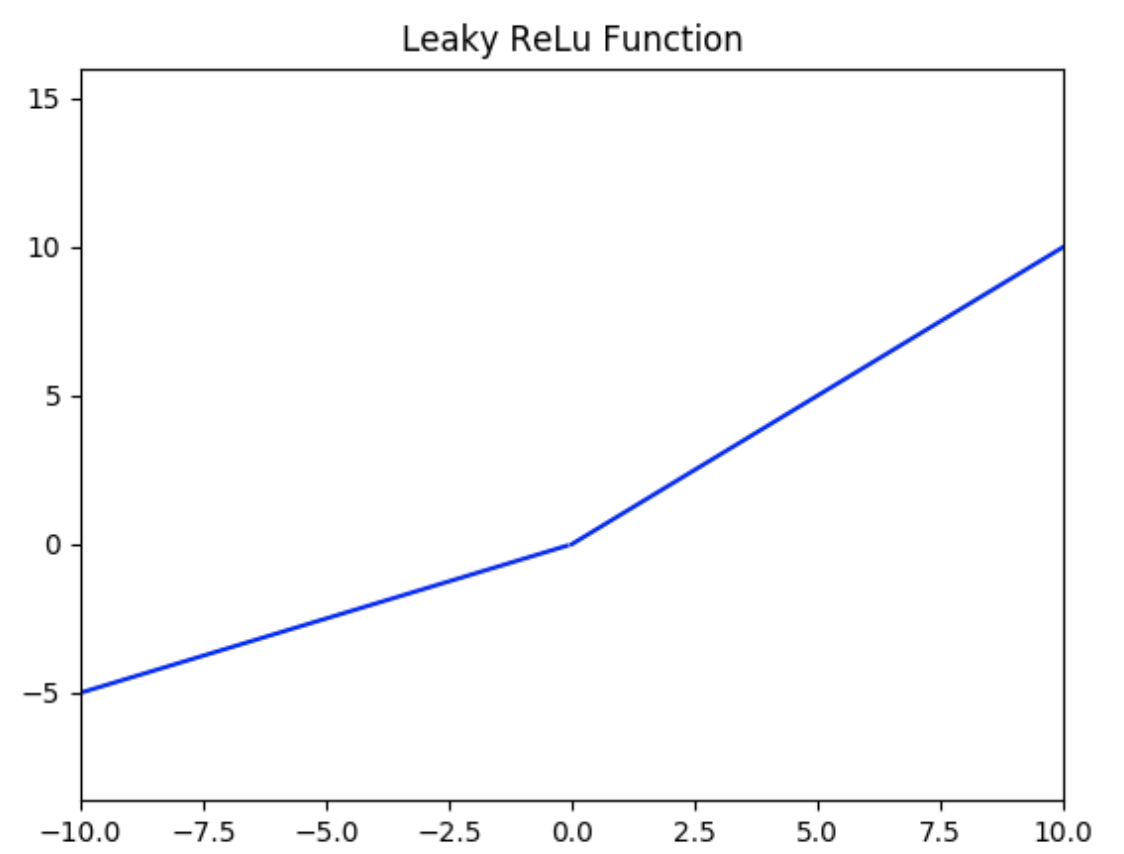
LeakyReLU的优势:
该方法与ReLU不同的是在 x x x小于0的时候取 f ( x ) = a x f(x) = ax f(x)=ax,其中 a a a是一个非常小的斜率(比如0.01)。这样的改进可以使得当 x x x小于0的时候也不会导致反向传播时的梯度消失现象。
LeakyReLU的不足:
- 无法避免梯度爆炸的问题。
- 神经网络不学习 α \alpha α值。
- 在求导的时候,两部分都是线性的。
SoftPlus激活函数
SoftPlus激活函数的定义为:
f ( x ) = l n ( 1 + e x ) f(x) = ln( 1 + e^x) f(x)=ln(1+ex)
值域为 ( 0 , + ∞ ) (0,+∞) (0,+∞)。
函数图像如下:
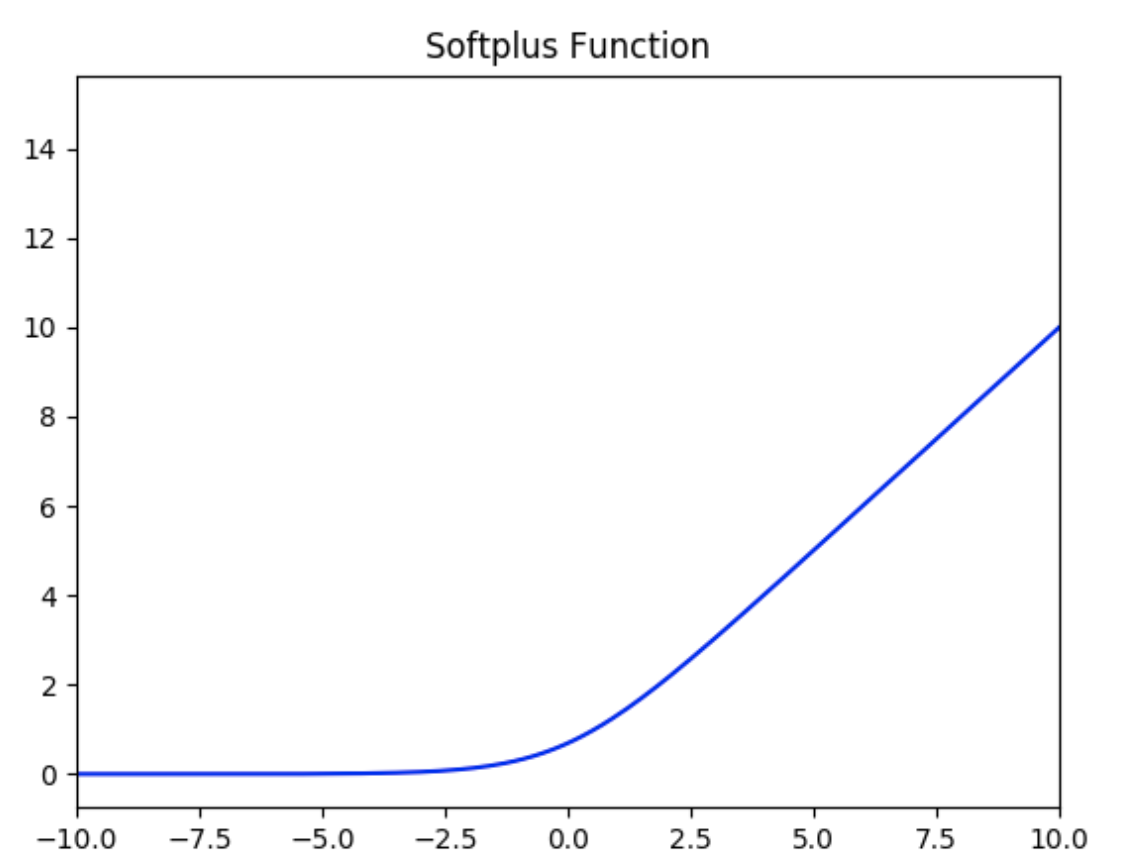
可以把SoftPlus看作是ReLU的平滑。
ELU激活函数
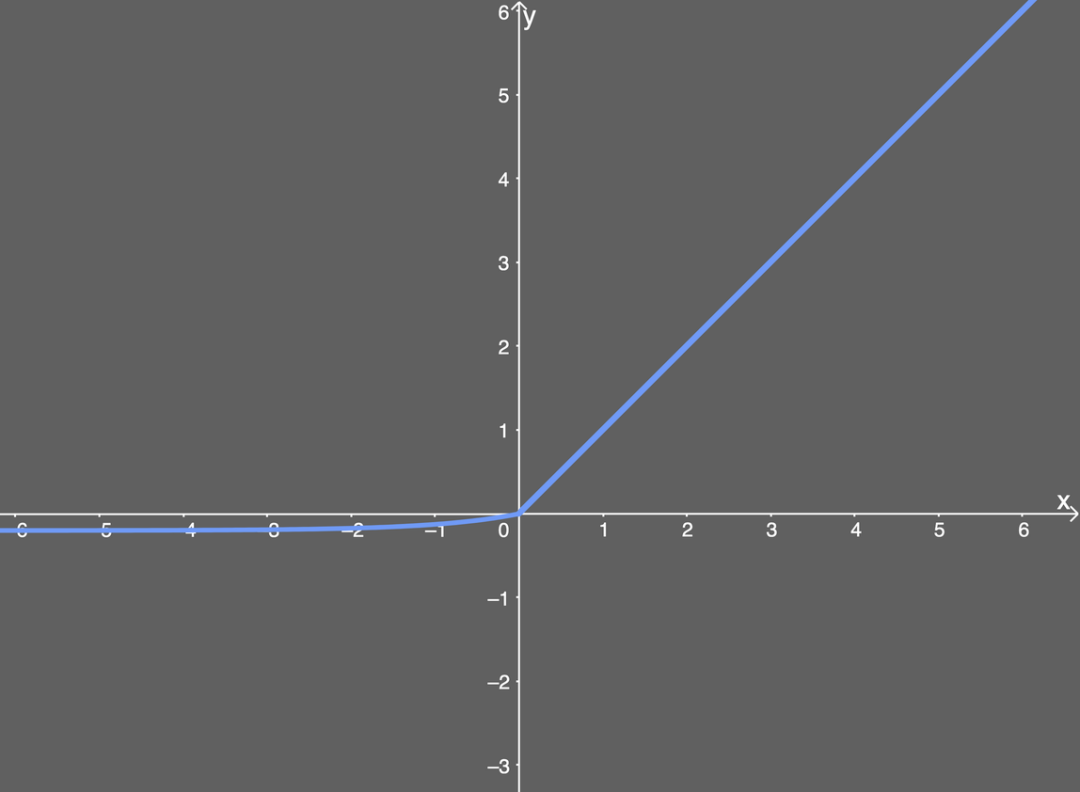
ELU激活函数解决了ReLU的一些问题,同时也保留了一些好的方面。这种激活函数要选取一个 α \alpha α值,其常见的取值是在0.1到0.3之间。
函数定义如下所示:
f ( x ) = { a ( e x − 1 ) , x < 0 x , x ≥ 0 f(x) = \left\{ \begin{aligned} a(e^x -1), \quad x<0 \\ x, \quad x\ge0 \end{aligned} \right. f(x)={a(ex−1),x<0x,x≥0
如果我们输入的 x x x值大于 0 0 0,则结果与ReLU一样,即 y y y值等于 x x x值;但如果输入的 x x x值小于 0 0 0,则我们会得到一个稍微小于 0 0 0的值,所得到的 y y y值取决于输入的 x x x值,但还要兼顾参数 α \alpha α——可以根据需要来调整这个参数。公式进一步引入了指数运算 e x e^x ex,因此ELU的计算成本比ReLU高。
下面给出了 α \alpha α值为0.2时的ELU函数图:
ELU的导数:
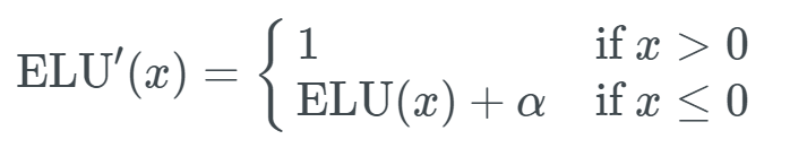
导数图如下所示:
ELU的优势:
- 能避免ReLU中一些神经元无法更新的情况。
- 能得到负值输出。
ELU的不足:
- 包含指数运算,计算时间长。
- 无法避免梯度爆炸问题。
- 神经网络无法学习 α \alpha α值。
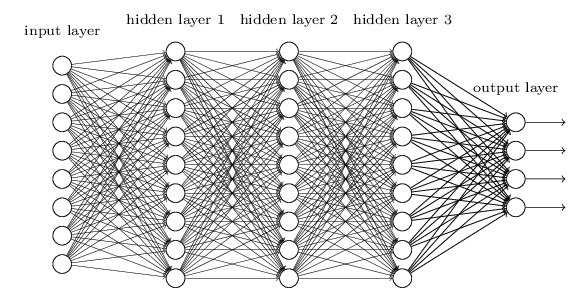
【十一】反向传播算法(BP)的概念及简单推导
反向传播(Backpropagation,BP)算法是一种与最优化方法(如梯度下降法)结合使用的,用来训练人工神经网络的常见算法。BP算法对网络中所有权重计算损失函数的梯度,并将梯度反馈给最优化方法,用来更新权值以最小化损失函数。该算法会先按前向传播方式计算(并缓存)每个节点的输出值,然后再按反向传播遍历图的方式计算损失函数值相对于每个参数的偏导数。
接下来我们以全连接层,使用sigmoid激活函数,Softmax+MSE作为损失函数的神经网络为例,推导BP算法逻辑。由于篇幅限制,这里只进行简单推导,后续Rocky将专门写一篇PB算法完整推导流程,大家敬请期待。
首先,我们看看sigmoid激活函数的表达式及其导数:
s
i
g
m
o
i
d
表达式:
σ
(
x
)
=
1
1
+
e
−
x
sigmoid表达式:\sigma(x) = \frac{1}{1+e^{-x}}
sigmoid表达式:σ(x)=1+e−x1
s
i
g
m
o
i
d
导数:
d
d
x
σ
(
x
)
=
σ
(
x
)
−
σ
(
x
)
2
=
σ
(
1
−
σ
)
sigmoid导数:\frac{d}{dx}\sigma(x) = \sigma(x) - \sigma(x)^2 = \sigma(1- \sigma)
sigmoid导数:dxdσ(x)=σ(x)−σ(x)2=σ(1−σ)
可以看到sigmoid激活函数的导数最终可以表达为输出值的简单运算。
我们再看MSE损失函数的表达式及其导数:
M S E 损失函数的表达式: L = 1 2 ∑ k = 1 K ( y k − o k ) 2 MSE损失函数的表达式:L = \frac{1}{2}\sum^{K}_{k=1}(y_k - o_k)^2 MSE损失函数的表达式:L=21k=1∑K(yk−ok)2
其中 y k y_k yk代表ground truth(gt)值, o k o_k ok代表网络输出值。
M S E 损失函数的偏导: ∂ L ∂ o i = ( o i − y i ) MSE损失函数的偏导:\frac{\partial L}{\partial o_i} = (o_i - y_i) MSE损失函数的偏导:∂oi∂L=(oi−yi)
由于偏导数中单且仅当 k = i k = i k=i时才会起作用,故进行了简化。
接下来我们看看全连接层输出的梯度:
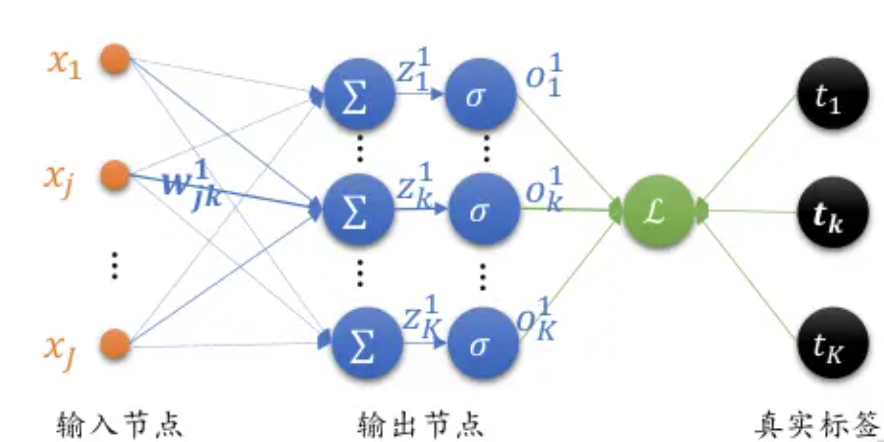
M S E 损失函数的表达式: L = 1 2 ∑ i = 1 K ( o i 1 − t i ) 2 MSE损失函数的表达式:L = \frac{1}{2}\sum^{K}_{i=1}(o_i^1 - t_i)^2 MSE损失函数的表达式:L=21i=1∑K(oi1−ti)2
M S E 损失函数的偏导: ∂ L ∂ w j k = ( o k − t k ) o k ( 1 − o k ) x j MSE损失函数的偏导:\frac{\partial L}{\partial w_{jk}} = (o_k - t_k)o_k(1-o_k)x_j MSE损失函数的偏导:∂wjk∂L=(ok−tk)ok(1−ok)xj
我们用 δ k = ( o k − t k ) o k ( 1 − o k ) \delta_k = (o_k - t_k)o_k(1-o_k) δk=(ok−tk)ok(1−ok),则能再次简化:
M S E 损失函数的偏导: d L d w j k = δ k x j MSE损失函数的偏导:\frac{dL}{dw_{jk}} = \delta_kx_j MSE损失函数的偏导:dwjkdL=δkxj
最后,我们看看那PB算法中每一层的偏导数:
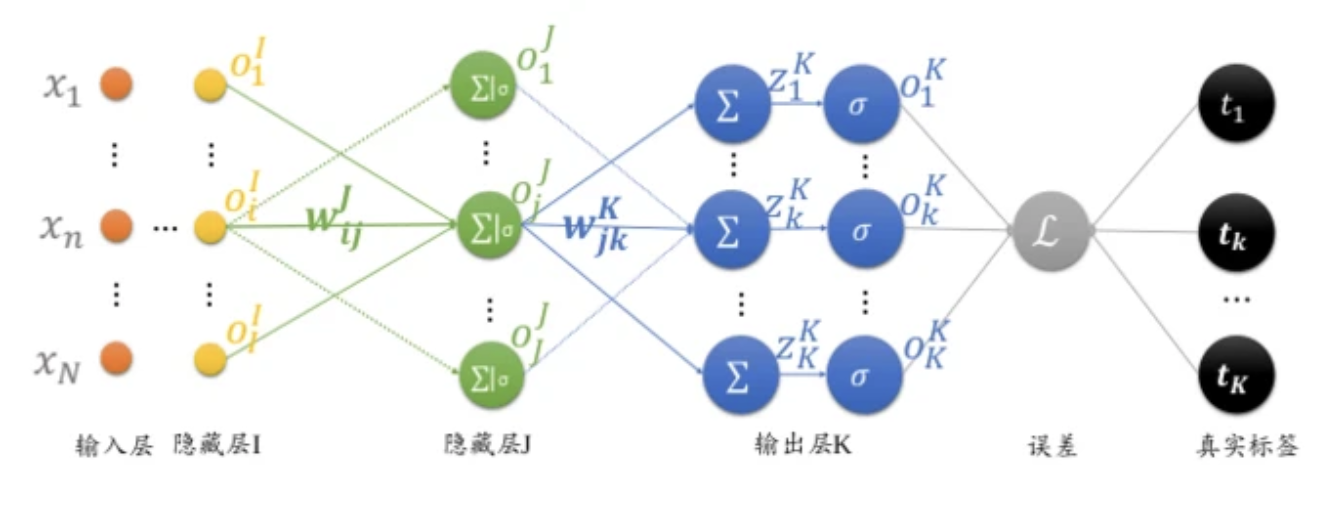
输出层:
∂
L
∂
w
j
k
=
δ
k
K
o
j
\frac{\partial L}{\partial w_{jk}} = \delta_k^K o_j
∂wjk∂L=δkKoj
δ
k
K
=
(
o
k
−
t
k
)
o
k
(
1
−
o
k
)
\delta_k^K = (o_k - t_k)o_k(1-o_k)
δkK=(ok−tk)ok(1−ok)
倒数第二层:
∂
L
∂
w
i
j
=
δ
j
J
o
i
\frac{\partial L}{\partial w_{ij}} = \delta_j^J o_i
∂wij∂L=δjJoi
δ
j
J
=
o
j
(
1
−
o
j
)
∑
k
δ
k
K
w
j
k
\delta_j^J = o_j(1 - o_j) \sum_{k}\delta_k^Kw_{jk}
δjJ=oj(1−oj)k∑δkKwjk
倒数第三层:
∂
L
∂
w
n
i
=
δ
i
I
o
n
\frac{\partial L}{\partial w_{ni}} = \delta_i^I o_n
∂wni∂L=δiIon
δ
i
I
=
o
i
(
1
−
o
i
)
∑
j
δ
j
J
w
i
j
\delta_i^I = o_i(1 - o_i) \sum_{j}\delta_j^Jw_{ij}
δiI=oi(1−oi)j∑δjJwij
像这样依次往回推导,再通过梯度下降算法迭代优化网络参数,即可走完PB算法逻辑。
【十二】分组卷积的相关知识
分组卷积(Group Convolution)最早出现在AlexNet网络中,分组卷积被用来切分网络,使其能在多个GPU上并行运行。

普通卷积进行运算的时候,如果输入feature map尺寸是 C × H × W C\times H \times W C×H×W,卷积核有N个,那么输出的feature map与卷积核的数量相同也是N个,每个卷积核的尺寸为 C × K × K C\times K \times K C×K×K,N个卷积核的总参数量为 N × C × K × K N \times C \times K \times K N×C×K×K。
分组卷积的主要对输入的feature map进行分组,然后每组分别进行卷积。如果输入feature map尺寸是 C × H × W C\times H \times W C×H×W,输出feature map的数量为 N N N个,如果我们设定要分成G个group,则每组的输入feature map数量为 C G \frac{C}{G} GC,则每组的输出feature map数量为 N G \frac{N}{G} GN,每个卷积核的尺寸为 C G × K × K \frac{C}{G} \times K \times K GC×K×K,卷积核的总数仍为N个,每组的卷积核数量为 N G \frac{N}{G} GN,卷积核只与其同组的输入map进行卷积,卷积核的总参数量为 N × C G × K × K N \times \frac{C}{G} \times K \times K N×GC×K×K,易得总的参数量减少为原来的 1 G \frac{1}{G} G1。
分组卷积的作用:
- 分组卷积可以减少参数量。
- 分组卷积可以看成是稀疏操作,有时可以在较少参数量的情况下获得更好的效果(相当于正则化操作)。
- 当分组数量等于输入feature map通道数量,输出feature map数量也等于输入feature map数量时,分组卷积就成了Depthwise卷积,可以使参数量进一步缩减。
----【经典模型&&热门模型】----
【一】Focal Loss的作用?
Focal Loss是解决了分类问题中类别不均衡、分类难度差异的一个损失函数,使得模型在训练过程中更加聚焦在困难样本上。
Focal Loss是从二分类问题出发,同样的思想可以迁移到多分类问题上。
我们知道二分类问题的标准loss是交叉熵:
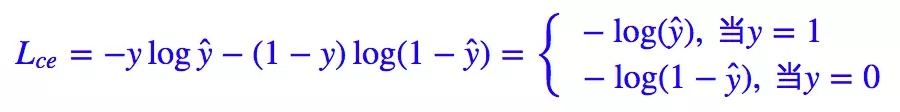
对于二分类问题我们也几乎适用sigmoid激活函数
y
^
=
σ
(
x
)
\hat{y} = \sigma(x)
y^=σ(x),所以上面的式子可以转化成:
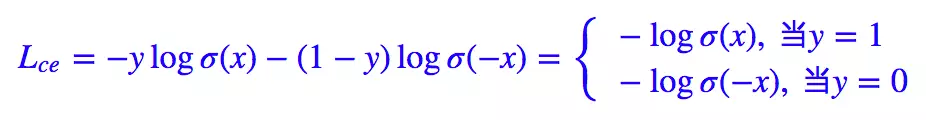
这里有
1
−
σ
(
x
)
=
σ
(
−
x
)
1 - \sigma(x) = \sigma(-x)
1−σ(x)=σ(−x)。
Focal Loss论文中给出的式子如下:

其中 y ∈ { 1 , − 1 } y\in \{ 1,-1\} y∈{1,−1}是真实标签, p ∈ [ 0 , 1 ] p\in[0,1] p∈[0,1]是预测概率。
我们再定义 p t : p_{t}: pt:

那么,上面的交叉熵的式子可以转换成:

有了上面的铺垫,最初Focal Loss论文中接着引入了均衡交叉熵函数:

针对类别不均衡问题,在Loss里加入一个控制权重,对于属于少数类别的样本,增大 α t \alpha_{t} αt即可。但这样有一个问题,它仅仅解决了正负样本之间的平衡问题,并没有区分易分/难分样本。
为什么上述公式只解决正负样本不均衡问题呢?
因为增加了一个系数 α t \alpha_{t} αt,跟 p t p_{t} pt的定义类似,当 l a b e l = 1 label=1 label=1的时候 α t = α \alpha_{t}=\alpha αt=α ;当 l a b e l = − 1 label=-1 label=−1的时候, α t = 1 − α \alpha_{t}= 1 - \alpha αt=1−α, α \alpha α的范围也是 [ 0 , 1 ] [0,1] [0,1]。因此可以通过设定 α \alpha α的值(如果 1 1 1这个类别的样本数比 − 1 -1 −1这个类别的样本数少很多,那么 α \alpha α可以取 0.5 0.5 0.5到 1 1 1来增加 1 1 1这个类的样本的权重)来控制正负样本对整体Loss的贡献。
Focal Loss
为了可以区分难/易样本,Focal Loss雏形就出现了:

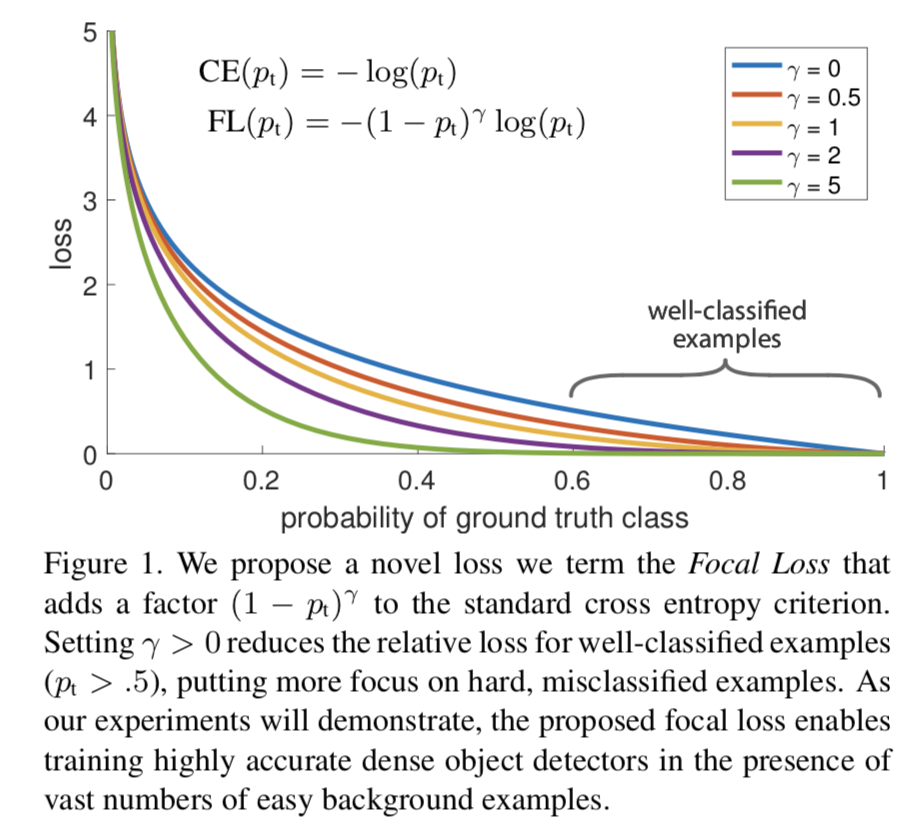
( 1 − p t ) γ (1 - p_{t})^{\gamma} (1−pt)γ用于平衡难易样本的比例不均, γ > 0 \gamma >0 γ>0起到了对 ( 1 − p t ) (1 - p_{t}) (1−pt)的放大作用。 γ > 0 \gamma >0 γ>0减少易分样本的损失,使模型更关注于困难易错分的样本。例如当 γ = 2 \gamma =2 γ=2时,模型对于某正样本预测置信度 p t p_{t} pt为 0.9 0.9 0.9,这时 ( 1 − 0.9 ) γ = 0.01 (1 - 0.9)^{\gamma} = 0.01 (1−0.9)γ=0.01,也就是FL值变得很小;而当模型对于某正样本预测置信度 p t p_{t} pt为0.3时, ( 1 − 0.3 ) γ = 0.49 (1 - 0.3)^{\gamma} = 0.49 (1−0.3)γ=0.49,此时它对Loss的贡献就变大了。当 γ = 0 \gamma = 0 γ=0时变成交叉熵损失。
为了应对正负样本不均衡的问题,在上面的式子中再加入平衡交叉熵的 α t \alpha_{t} αt因子,用来平衡正负样本的比例不均,最终得到Focal Loss:
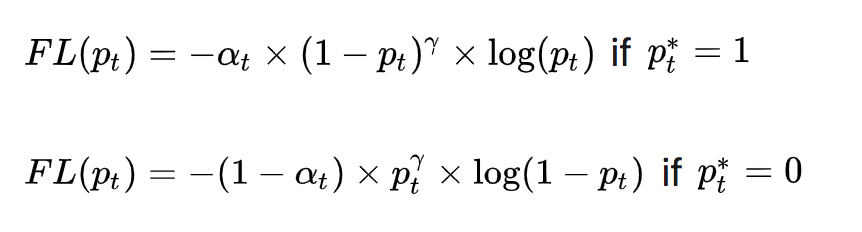
Focal Loss论文中给出的实验最佳取值为 a t = 0.25 a_{t}= 0.25 at=0.25, γ = 2 \gamma = 2 γ=2。
【二】YOLO系列的面试问题
Rocky之前总结了YOLOv1-v7全系列的解析文章,帮助大家应对可能出现的与YOLO相关的面试问题,大家可按需取用:
【Make YOLO Great Again】YOLOv1-v7全系列大解析(汇总篇)
【三】有哪些经典的轻量型人脸检测模型?
人脸检测相对于通用目标检测来说,算是一个子任务。比起通用目标检测任务动辄检测1000个类别,人脸检测任务主要聚焦于人脸的单类目标检测,使用通用目标检测模型太过奢侈,有点“杀鸡用牛刀”的感觉,并且大量的参数冗余,会影响部署侧的实用性,故针对人脸检测任务,学术界提出了很多轻量型的人脸检测模型,Rocky在这里给大家介绍一些比较有代表性的:
- libfacedetection
- Ultra-Light-Fast-Generic-Face-Detector-1MB
- A-Light-and-Fast-Face-Detector-for-Edge-Devices
- CenterFace
- DBFace
- RetinaFace
- MTCNN
【四】LFFD人脸检测模型的结构和特点?
Rocky在实习/校招面试中被多次问到LFFD模型以及面试官想套取LFFD相关算法方案的情况,说明LFFD模型在工业界还是比较有价值的,下面Rocky就带着大家学习一下LFFD模型的知识:
LFFD(A-Light-and-Fast-Face-Detector-for-Edge-Devices)适用于人脸、行人、车辆等单目标检测任务,具有速度快,模型小,效果好的特点。LFFD是Anchor-free的方法,使用感受野替代Anchors,并在主干结构上抽取8路特征图对从小到大的人脸进行检测,检测模块分为类别二分类与边界框回归。
LFFD模型结构
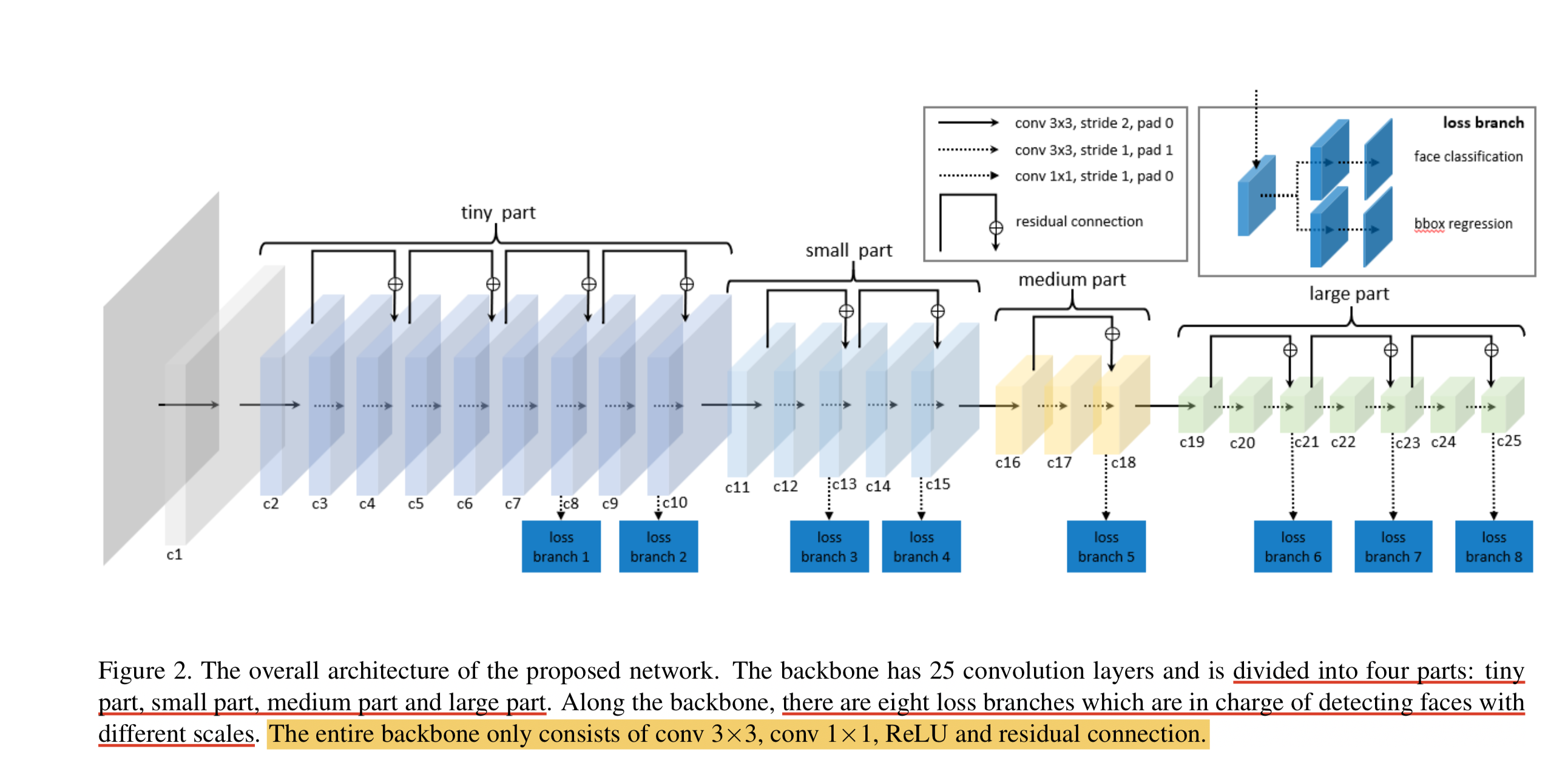
我们可以看到,LFFD模型主要由四部分组成:tiny part、small part、medium part、large part。
模型中并没有采用BN层,因为BN层会减慢17%的推理速度。其主要采用尽可能快的下采样来保持100%的人脸覆盖。
LFFD主要特点:
-
结构简单直接,易于在主流AI端侧设备中进行部署。
-
检测小目标能力突出,在极高分辨率(比如8K或更大)画面,可以检测其间10个像素大小的目标;
LFFD损失函数
LFFD损失函数是由regression loss和classification loss的加权和。
分类损失使用了交叉熵损失。
回归损失使用了L2损失函数。
LFFD论文地址:LFFD: A Light and Fast Face Detector for Edge Devices论文地址
【五】U-Net模型的结构和特点?
U-Net网络结构如下所示:
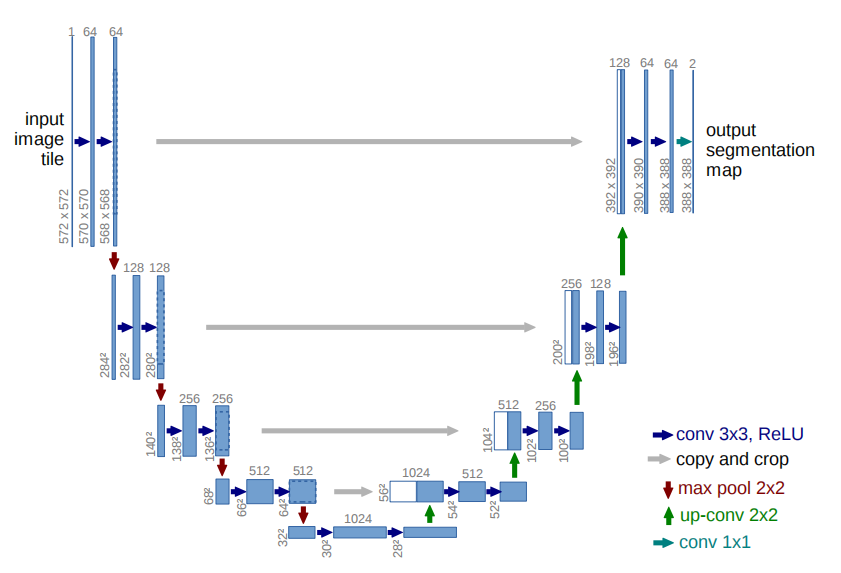
U-Net网络的特点:
- 全卷积神经网络:使用 1 × 1 1\times1 1×1卷积完全取代了全连接层,使得模型的输入尺寸不受限制。
- 左半部分网络是收缩路径(contracting path):使用卷积和max pooling层,对feature map进行下采样。
- 右半部分网络是扩张路径(expansive path):使用转置卷积对feature map进行上采样,并将其与收缩路径对应层产生的特征图进行concat操作。上采样可以补充特征信息,加上与左半部分网络收缩路径的特征图进行concat(通过crop操作使得两个特征图尺寸一致),这就相当于在高分辨率和高维特征当中做一个融合折中。
- U-Net提出了让人耳目一新的编码器-解码器整体结构,让U-Net充满了生命力与强适应性。
U-Net在医疗图像,缺陷检测以及交通场景中有非常丰富的应用,可以说图像分割实际场景,U-Net是当仁不让的通用Baseline。
U-Net的论文地址:U-Net
【六】RepVGG模型的结构和特点?
RepVGG模型的基本架构由20多层 3 × 3 3\times3 3×3卷积组成,分成5个stage,每个stage的第一层是stride=2的降采样,每个卷积层用ReLU作为激活函数。
RepVGG的主要特点:
- 3 × 3 3\times3 3×3卷积在GPU上的计算密度(理论运算量除以所用时间)可达1x1和5x5卷积的四倍.
- 直筒型单路结构的计算效率比多路结构高。
- 直筒型单路结构比起多路结构内存占用少。
- 单路架构灵活性更好,容易进一步进行模型压缩等操作。
- RepVGG中只含有一种算子,方便芯片厂商设计专用芯片来提高端侧AI效率。
那么是什么让RepVGG能在上述情形下达到SOTA效果呢?
答案就是结构重参数化(structural re-parameterization)。
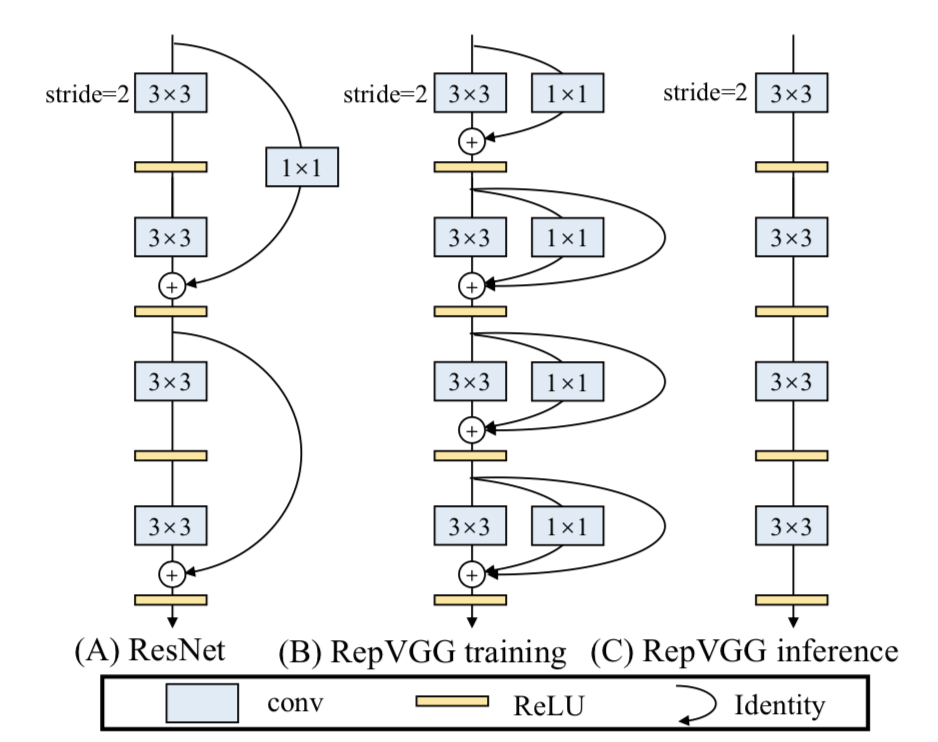
在训练阶段,训练一个多分支模型,并将多分支模型等价转换为单路模型。在部署阶段,部署单路模型即可。这样就可以同时利用多分支模型训练时的优势(性能高)和单路模型推理时的好处(速度快、省内存)。
更多结构重参数化细节知识将在后续的篇章中展开介绍,大家尽情期待!
【七】GAN的核心思想?
2014年,Ian Goodfellow第一次提出了GAN的概念。Yann LeCun曾经说过:“生成对抗网络及其变种已经成为最近10年以来机器学习领域最为重要的思想之一”。GAN的提出让生成式模型重新站在了深度学习这个浪潮的璀璨舞台上,与判别式模型开始谈笑风生。
GAN由生成器 G G G和判别器 D D D组成。其中,生成器主要负责生成相应的样本数据,输入一般是由高斯分布随机采样得到的噪声 Z Z Z。而判别器的主要职责是区分生成器生成的样本与 g t ( G r o u n d T r u t h ) gt(GroundTruth) gt(GroundTruth)样本,输入一般是 g t gt gt样本与相应的生成样本,我们想要的是对 g t gt gt样本输出的置信度越接近 1 1 1越好,而对生成样本输出的置信度越接近 0 0 0越好。与一般神经网络不同的是,GAN在训练时要同时训练生成器与判别器,所以其训练难度是比较大的。
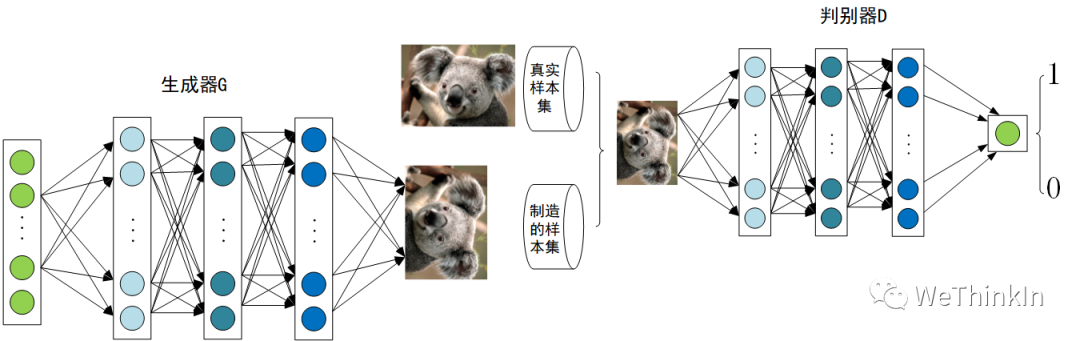
在提出GAN的第一篇论文中,生成器被比喻为印假钞票的犯罪分子,判别器则被当作警察。犯罪分子努力让印出的假钞看起来逼真,警察则不断提升对于假钞的辨识能力。二者互相博弈,随着时间的进行,都会越来越强。在图像生成任务中也是如此,生成器不断生成尽可能逼真的假图像。判别器则判断图像是 g t gt gt图像,还是生成的图像。二者不断博弈优化,最终生成器生成的图像使得判别器完全无法判别真假。
GAN的对抗思想主要由其目标函数实现。具体公式如下所示:
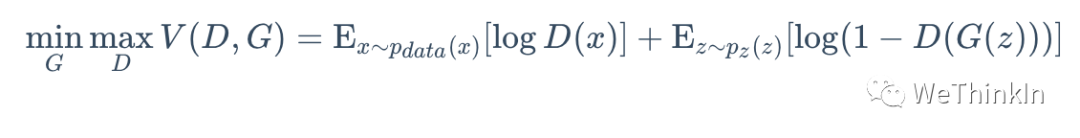
上面这个公式看似复杂,其实不然。跳出细节来看,整个公式的核心逻辑其实就是一个min-max问题,深度学习数学应用的边界扩展到这里,GAN便开始发光了。
接着我们再切入细节。我们可以分两部分开看这个公式,即判别器最小化角度与生成器最大化角度。在判别器角度,我们希望最大化这个目标函数,因为在公示第一部分,其表示 g t gt gt样本 ( x ~ P d a t a ) (x ~Pdata) (x~Pdata)输入判别器后输出的置信度,当然是越接近 1 1 1越好。而公式的第二部分表示生成器输出的生成样本 ( G ( z ) ) (G(z)) (G(z))再输入判别器中进行进行二分类判别,其输出的置信度当然是越接近 0 0 0越好,所以 1 − D ( G ( z ) ) 1 - D(G(z)) 1−D(G(z))越接近 1 1 1越好。
在生成器角度,我们想要最小化判别器目标函数的最大值。判别器目标函数的最大值代表的是真实数据分布与生成数据分布的JS散度,JS散度可以度量分布的相似性,两个分布越接近,JS散度越小(JS散度是在初始GAN论文中被提出,实际应用中会发现有不足的地方,后来的论文陆续提出了很多的新损失函数来进行优化)
写到这里,大家应该就明白GAN的对抗思想了,下面是初始GAN论文中判别器与生成器损失函数的具体设置以及训练的具体流程:

在图中可以看出,将判别器损失函数离散化,其与交叉熵的形式一致,我们也可以说判别器的目标是最小化交叉熵损失。
【八】面试常问的经典GAN模型?
- 原始GAN及其训练逻辑
- DCGAN
- CGAN
- WGAN
- LSGAN
- PixPix系列
- CysleGAN
- SRGAN系列
【九】FPN(Feature Pyramid Network)的相关知识
FPN的创新点
- 设计特征金字塔的结构
- 提取多层特征(bottom-up,top-down)
- 多层特征融合(lateral connection)
设计特征金字塔的结构,用于解决目标检测中的多尺度问题,在基本不增加原有模型计算量的情况下,大幅度提升小物体(small object)的检测性能。
原来很多目标检测算法都是只采用高层特征进行预测,高层的特征语义信息比较丰富,但是分辨率较低,目标位置比较粗略。假设在深层网络中,最后的高层特征图中一个像素可能对应着输出图像 20 × 20 20 \times 20 20×20的像素区域,那么小于 20 × 20 20 \times 20 20×20像素的小物体的特征大概率已经丢失。与此同时,低层的特征语义信息比较少,但是目标位置准确,这是对小目标检测有帮助的。FPN将高层特征与底层特征进行融合,从而同时利用低层特征的高分辨率和高层特征的丰富语义信息,并进行了多尺度特征的独立预测,对小物体的检测效果有明显的提升。
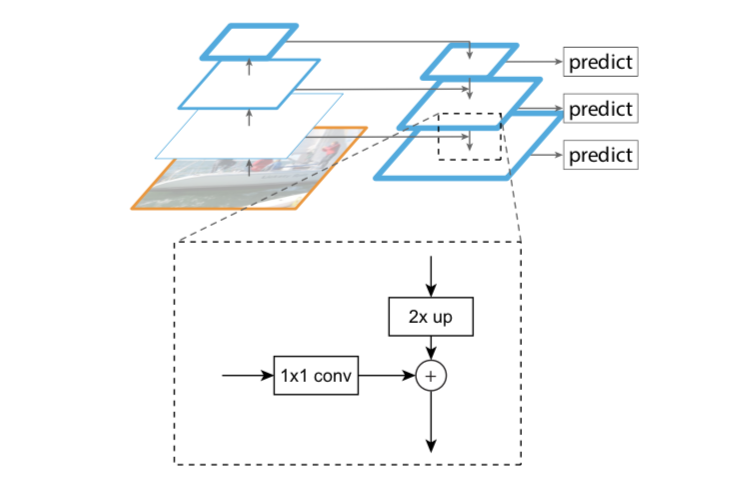
传统解决这个问题的思路包括:
- 图像金字塔(image pyramid),即多尺度训练和测试。但该方法计算量大,耗时较久。
- 特征分层,即每层分别输出对应的scale分辨率的检测结果,如SSD算法。但实际上不同深度对应不同层次的语义特征,浅层网络分辨率高,学到更多是细节特征,深层网络分辨率低,学到更多是语义特征,单单只有不同的特征是不够的。
FPN的主要模块
- Bottom-up pathway(自底向上线路)
- Top-down path(自顶向下线路)
- Lareral connections(横向链路)
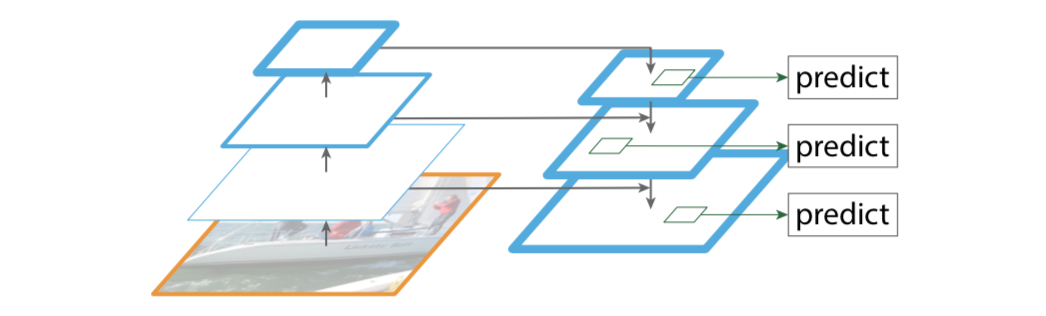
Bottom-up pathway(自底向上线路)
自底向上线路是卷积网络的前向传播过程。在前向传播过程中,feature map的大小可以在某些层发生改变。
Top-down path(自顶向下线路)和Lareral connections(横向链路)
自顶向下线路是上采样的过程,而横向链路是将自顶向下线路的结果和自底向上线路的结构进行融合。
上采样的feature map与相同大小的下采样的feature map进行逐像素相加融合(element-wise addition),其中自底向上的feature先要经过 1 × 1 1\times 1 1×1卷积层,目的是为了减少通道维度。
FPN应用
论文中FPN直接在Faster R-CNN上进行改进,其backbone是ResNet101,FPN主要应用在Faster R-CNN中的RPN和Fast R-CNN两个模块中。
FPN+RPN:
将FPN和RPN结合起来,那RPN的输入就会变成多尺度的feature map,并且在RPN的输出侧接多个RPN head层用于满足对anchors的分类和回归。
FPN+Fast R-CNN:
Fast R-CNN的整体结构逻辑不变,在backbone部分引入FPN思想进行改造。
【十】SPP(Spatial Pyramid Pooling)的相关知识
在目标检测领域,很多检测算法最后使用了全连接层,导致输入尺寸固定。当遇到尺寸不匹配的图像输入时,就需要使用crop或者warp等操作进行图像尺寸和算法输入的匹配。这两种方式可能出现不同的问题:裁剪的区域可能没法包含物体的整体;变形操作造成目标无用的几何失真等。
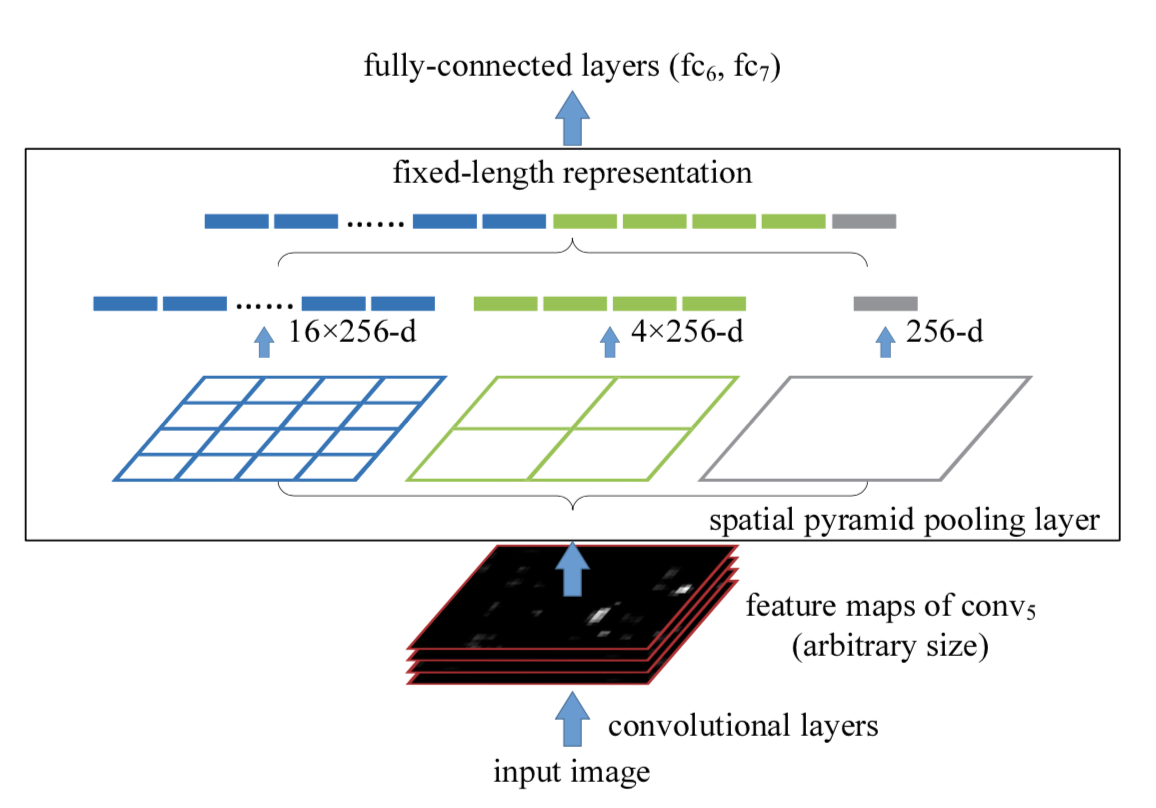
而SPP的做法是在卷积层后增加一个SPP layer,将features map拉成固定长度的feature vector。然后将feature vector输入到全连接层中。以此来解决上述的尴尬问题。
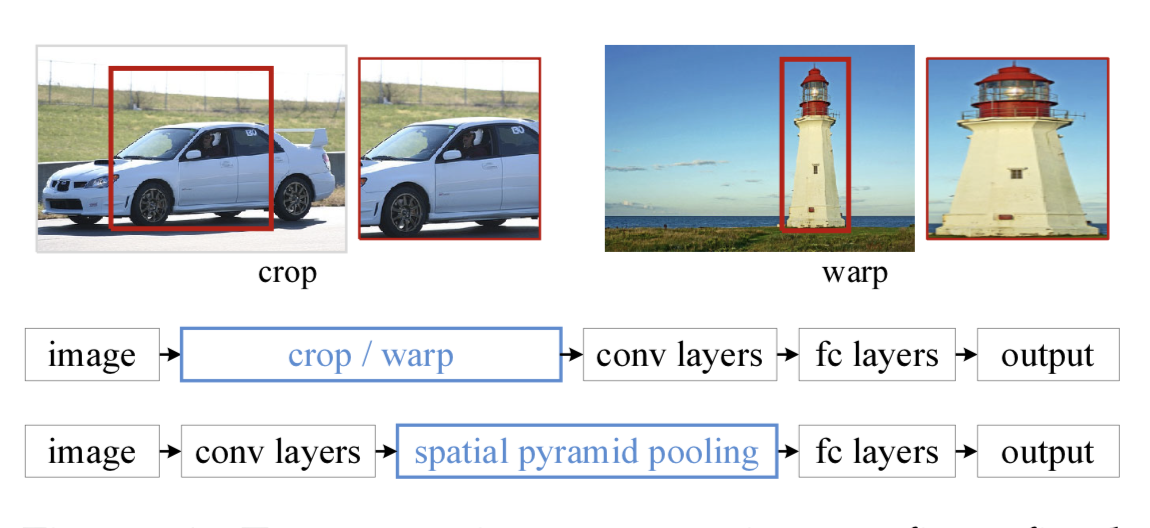
SPP的优点:
- SPP可以忽略输入尺寸并且产生固定长度的输出。
- SPP使用多种尺度的滑动核,而不是只用一个尺寸的滑动窗口进行pooling。
- SPP在不同尺寸feature map上提取特征,增大了提取特征的丰富度。
在YOLOv4中,对SPP进行了创新使用,Rocky已在【Make YOLO Great Again】YOLOv1-v7全系列大解析(Neck篇)中详细讲解,大家可按需取用~
【十一】目标检测中AP,AP50,AP75,mAP等指标的含义
AP:PR曲线下的面积。
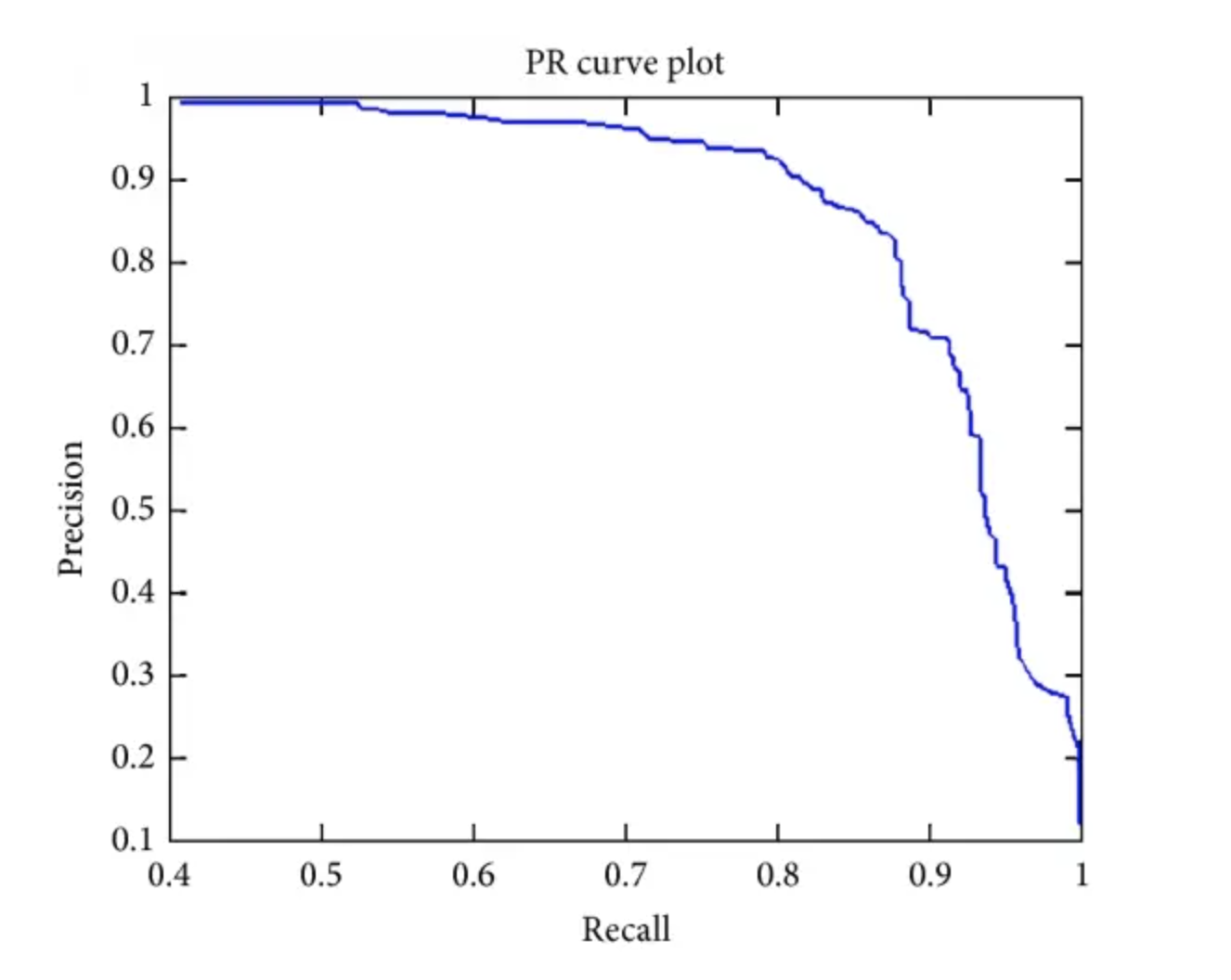
AP50: 固定IoU为50%时的AP值。
AP75:固定IoU为75%时的AP值。
AP@[0.5:0.95]:把IoU的值从50%到95%每隔5%进行了一次划分,并对这10组AP值取平均。
mAP:对所有的类别进行AP的计算,然后取均值。
mAP@[.5:.95](即mAP@[.5,.95]):表示在不同IoU阈值(从0.5到0.95,步长0.05)(0.5、0.55、0.6、0.65、0.7、0.75、0.8、0.85、0.9、0.95)上的平均mAP。
【十二】YOLOv2中的anchor如何生成?
YOLOv2中引入K-means算法进行anchor的生成,可以自动找到更好的anchor宽高的值用于模型训练的初始化。
但如果使用经典K-means中的欧氏距离作为度量,意味着较大的Anchor会比较小的Anchor产生更大的误差,聚类结果可能会偏离。
由于目标检测中主要关心anchor与ground true box(gt box)的IOU,不关心两者的大小。因此,使用IOU作为度量更加合适,即提高IOU值。因此YOLOv2采用IOU值为评判标准:
d ( g t b o x , a n c h o r ) = 1 − I O U ( g t b o x , a n c h o r ) d(gt box,anchor) = 1 - IOU(gt box,anchor) d(gtbox,anchor)=1−IOU(gtbox,anchor)
具体anchor生成步骤与经典K-means大致相同,在下一个章节中会详细介绍。主要的不同是使用的度量是 d ( g t b o x , a n c h o r ) d(gt box,anchor) d(gtbox,anchor),并将anchor作为簇的中心。
----【机器学习基础】----
【一】机器学习有哪些种类?
机器学习中通常根据数据是否有标签可以分为监督学习(supervised learning)、非监督学习(unsupervised learning),半监督学习(semi-supervised learning)以及弱监督学习(weakly supervised learning)。
监督学习
机器学习模型在训练过程中的所有数据都有标签,就是监督学习的逻辑。
监督学习是最常见的学习种类,常见场景为分类和回归问题。
深度学习模型大都数都遵从监督学习的流程,并且支持向量机(Support Vector Machine, SVM),朴素贝叶斯(Naive Bayes),逻辑回归(Logistic Regression),K近邻(K-Nearest Neighborhood, KNN),决策树(Decision Tree),随机森林(Random Forest),AdaBoost以及线性判别分析(Linear Discriminant Analysis, LDA)等也属于监督学习算法的范畴。
非监督学习
非监督学习与监督学习完全相反,机器学习模型在训练过程中的所有数据都是没有标签的,主要学习数据本身的一些特性。
比如想象一个人从来没有见过猫和狗,如果给他看了大量的猫和狗,虽然他还是没有猫和狗的概念,但是他是能够观察出每个物种的共性和两个物种间的区别的,并对这个两种动物予以区分。
半监督学习
半监督学习的逻辑是机器学习模型在训练过程中,部分数据有标签,与此同时另外一部分数据没有标签,并把这两种数据都利用起来用于训练。
弱监督学习
弱监督学习的逻辑是机器学习模型在训练过程中使用的数据的标签存在不可靠的情况。这里的不可靠可以是标注不正确,多重标记,标记不充分,局部标记,包含噪声等情况。一个直观的例子是相对于分割的标签来说,分类的标签就是弱标签。
【二】L1正则为什么比L2正则更容易产生稀疏解?
我们首先可以设目标函数为 L L L,目标函数中的权值参数为 w w w,那么目标函数和权值参数的关系如下所示:

如上图所示,最优的 w w w在绿色的点处,而且 w w w非零。
我们首先可以使用L2正则进行优化,新的目标函数: L + C W 2 L + CW^{2} L+CW2,示意图如下蓝线所示:
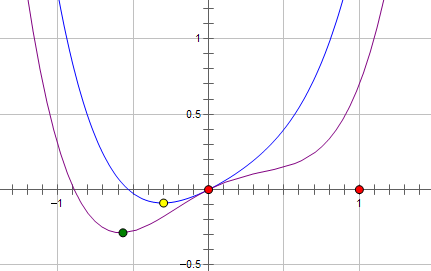
我们可以看到,最优的 w w w出现在黄点处, w w w的绝对值减小了,更靠近横坐标轴,但是依然是非零的。
为什么是非零的呢?
我们可以对L2正则下的目标函数求导:

我们发现,权重 w w w每次乘上的是小于1的倍数进行收敛,而且其导数在 w = 0 w=0 w=0时没有办法做到左右两边导数异号,所以L2正则使得整个训练过程稳定平滑,但是没有产生稀疏性。
接下来我们使用L1正则,新的目标函数: L + C ∣ w ∣ L + C|w| L+C∣w∣,示意图如下粉线所示:
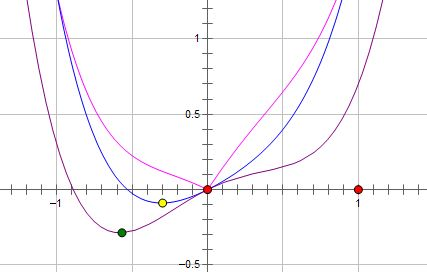
这里最优的 w w w就变成了0。因为保证使用L1正则后 x = 0 x=0 x=0处左右两个导数异号,就能满足极小值点形成的条件。
我们来看看这次目标函数求导的式子:

可以看出L1正则的惩罚很大, w w w每次都是减去一个常数的线性收敛,所以L1比L2更容易收敛到比较小的值,而如果 C > ∣ f ′ ( 0 ) ∣ C > |f^{'}(0)| C>∣f′(0)∣,就能保证 w = 0 w = 0 w=0处取得极小值。
上面只是一个权值参数 w w w。在深层网路中,L1会使得大量的 w w w最优值变成0,从而使得整个模型有了稀疏性。
【三】格拉姆矩阵的相关概念?
n维欧式空间中任意k个向量之间两两的内积所组成的矩阵,称为这k个向量的格拉姆矩阵(Gram matrix),这是一个对称矩阵。

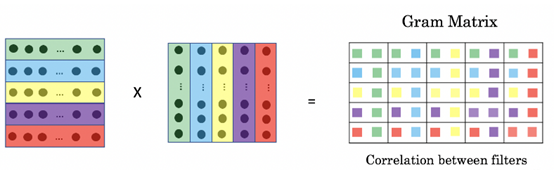
其中对角线元素提供了k个不同特征图(a1,a2 … ,ak)各自的信息,其余元素提供了不同特征图之间的相关信息。既能体现出有哪些特征,又能体现出不同特征间的紧密程度。图像风格迁移领域将其定义为风格特征。
格拉姆矩阵在风格迁移中有广泛的应用,深度学习中经典的风格迁移流程是:
-
准备基线图像和风格图像。
-
使用特征提取器分别提取基线图像和风格图像的feature map。
-
分别计算两个图像的feature map的格拉姆矩阵,以两个图像的格拉姆矩阵的差异最小化为优化目标,不断调整基线图像,使风格不断接近目标风格图像。
【四】感知损失的相关概念?
感知损失在图像生成领域中比较常用。其核心是将gt图片卷积得到的高层feature与生成图片卷积得到的高层feature进行回归,从而约束生成图像的高层特征(内容和全局结构)。
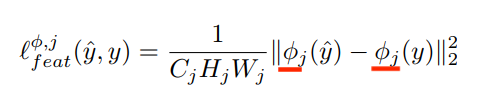
上面的公式中,划线部分代表了高层特征,一般使用VGG作为特征提取器。
【五】Accuracy、Precision、Recall、F1 Scores的相关概念?
首先Rocky介绍一下相关名词:
- TP(True Positive): 预测为正,实际为正
- FP(False Positive): 预测为正,实际为负
- TN(True Negative):预测为负,实际为负
- FN(false negative): 预测为负,实际为正
Accuracy、Precision、Recall、F1 Scores的公式如下所示:

Accuracy(准确率):分类正确的样本数占样本总数的比例。
Precision(精准度/查准率):当前预测为正样本类别中被正确分类的样本比例。
Recall(召回率/查全率):预测出来的正样本占正样本总数的比例。
F1-score是Precision和Recall的综合。F1-score越高,说明分类模型越稳健。
【六】梯度爆炸和梯度消失产生的原因及解决方法?
梯度爆炸和梯度消失问题
一般在深层神经网络中,我们需要预防梯度爆炸和梯度消失的情况。
梯度消失(gradient vanishing problem)和梯度爆炸(gradient exploding problem)一般随着网络层数的增加会变得越来越明显。
例如下面所示的含有三个隐藏层的神经网络,梯度消失问题发生时,接近输出层的hiden layer3的权重更新比较正常,但是前面的hidden layer1的权重更新会变得很慢,导致前面的权重几乎不变,仍然接近初始化的权重,这相当于hidden layer1没有学到任何东西,此时深层网络只有后面的几层网络在学习,而且网络在实际上也等价变成了浅层网络。
产生梯度爆炸和梯度消失问题的原因
我们来看看看反向传播的过程:
(假设网络每一层只有一个神经元,并且对于每一层 y i = σ ( z i ) = σ ( w i x i + b i ) y_{i} = \sigma(z_{i}) = \sigma(w_{i}x_{i} + b_{i}) yi=σ(zi)=σ(wixi+bi))

可以推导出:
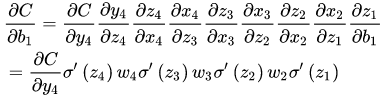
而sigmoid的导数 σ ′ ( x ) \sigma^{'}(x) σ′(x)如下图所示:
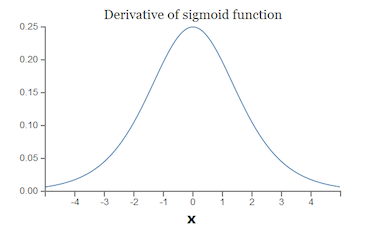
可以知道, σ ′ ( x ) \sigma^{'}(x) σ′(x)的最大值是 1 4 \frac{1}{4} 41,而我们初始化的权重 ∣ w ∣ |w| ∣w∣通常都小于1,因此 σ ′ ( x ) ∣ w ∣ < = 1 4 \sigma^{'}(x)|w| <= \frac{1}{4} σ′(x)∣w∣<=41,而且链式求导层数非常多,不断相乘的话,最后的结果越来越小,趋向于0,就会出现梯度消失的情况。
梯度爆炸则相反, σ ′ ( x ) ∣ w ∣ > 1 \sigma^{'}(x)|w| > 1 σ′(x)∣w∣>1时,不断相乘结果变得很大。
梯度爆炸和梯度消失问题都是因为网络太深,网络权重更新不稳定造成的,本质上是梯度方向传播的连乘效应。
梯度爆炸和梯度消失的解决方法
- 使用预训练加微调策略。
- 进行梯度截断。
- 使用ReLU、LeakyReLU等激活函数。
- 引入BN层。
- 使用残差结构。
- 使用LSTM思想。
【七】数据EDA逻辑(Exploratory Data Analysis)?
- 导入相应的Modules(numpy,pandas,matplotlib,PIL等)
- 阅读了解所有的数据文件(图片数据,类别文件,辅助文件等)
- 数据类别特征分析(数据类别总数,数据类别的平衡度,数据尺寸,噪声数据等)
- 数据可视化二次分析(直观了解不同类别的区别)
【八】K折交叉验证逻辑?
K折交叉验证的作用
当有多个不同的模型(结构不同、超参数不同等)可以选择时,我们通过K折交叉验证来选取对于特定数据集最好的模型。
K折交叉验证的流程
- 将含有 N N N个样本的数据集,分成 K K K份,每份含有 N K \frac{N}{K} KN个样本。选择其中一份作为验证集,另外 K − 1 K-1 K−1份作为训练集,验证集集就有 K K K种情况。
- 在每种情况中,用训练集训练模型,用验证集测试模型,计算模型的泛化误差。
- 交叉验证重复 K K K次,平均 K K K次的结果作为模型最终的泛化误差。
- K K K的取值一般在 [ 2 , 10 ] [2,10] [2,10]之间。 K K K折交叉验证的优势在于,同时重复运用随机产生的子样本进行训练和验证, 10 10 10折交叉验证是最常用的。
- 训练集中样本数量要足够多,一般至少大于总样本数的50%。
- 训练集和验证集必须从完整的数据集中均匀采样。均匀采样的目的是希望减少训练集、验证集与原数据集之间的偏差。当样本数量足够多时,通过随机采样,便可以实现均匀采样的效果。
5折交叉验证举例
5折交叉验证(5-fold cross-validation)用来验证从不同的模型中选取最优的模型(最合适的模型)。将数据集分成5份,轮流将其中4份作为训练数据,1份作为验证数据,进行试验。每次试验都会得出相应的正确率。5次的结果的正确率的平均值作为对算法精度的估计。同时对不同的模型(如CNN、SVM、LR等)做上述相同的操作,得出每个模型在特定数据集上的平均能力,从中选优。
例子:
假设我们有一个特定数据集,我们想从YOLOv4、Mask R-CNN、SSD、Faster R-CNN、RetinaNet这五个模型中选取在这个特定数据集中有最好效果的一个模型作为baseline,我们可以进行交叉验证来进行判断:
步骤:
- 将数据集分成5份。
- 对于每一个模型,for i = 1, 2, 3, 4,5,每个for循环里将除了第i份的所有数据作为训练集用于训练,得到参数;再将参数在第i份数据上进行验证,得到评价结果。
- 最后我们可以得到5个模型的结果,每个模型有5个验证结果。将每个模型的结果取平均值,得到该模型的平均结果。
- 5个模型中平均结果最好的模型就是我们想要的最优模型。
【九】KL散度相关概念
KL散度(Kullback-Leibler divergence),可以以称作相对熵(relative entropy)或信息散度(information divergence)。KL散度的理论意义在于度量两个概率分布之间的差异程度,当KL散度越大的时候,说明两者的差异程度越大;而当KL散度小的时候,则说明两者的差异程度小。如果两者相同的话,则该KL散度应该为0。
接下来我们举一个具体的🌰:
我们设定两个概率分布分别为 P P P和 Q Q Q,在设定为连续随机变量的前提下,他们对应的概率密度函数分别为 p ( x ) p(x) p(x)和 q ( x ) q(x) q(x)。如果我们用 q ( x ) q(x) q(x)去近似 p ( x ) p(x) p(x),则KL散度可以表示为:
K L ( P ∣ ∣ Q ) = ∫ p ( x ) log p ( x ) q ( x ) d x KL(P||Q) = \int p(x)\log \frac{p(x)}{q(x)}dx KL(P∣∣Q)=∫p(x)logq(x)p(x)dx
从上面的公式可以看出,当且仅当 P = Q P=Q P=Q时, K L ( P ∣ ∣ Q ) = 0 KL(P||Q) = 0 KL(P∣∣Q)=0。此外我们可以知道KL散度具备非负性,即 K L ( P ∣ ∣ Q ) > = 0 KL(P||Q) >= 0 KL(P∣∣Q)>=0。并且从公式中我们也发现,KL散度不具备对称性,也就是说 P P P对于 Q Q Q的KL散度并不等于 Q Q Q对于 P P P的KL散度。因此,KL散度并不是一个度量(metric),即KL散度并非距离。
我们再来看看离散的情况下用 q ( x ) q(x) q(x)去近似 p ( x ) p(x) p(x)的KL散度的公式:
K L ( P ∣ ∣ Q ) = ∑ p ( x ) log p ( x ) q ( x ) KL(P||Q) = \sum p(x)\log \frac{p(x)}{q(x)} KL(P∣∣Q)=∑p(x)logq(x)p(x)
接下来我们对上面的式子进行展开:
K L ( P ∣ ∣ Q ) = ∑ p ( x ) log p ( x ) q ( x ) = − ∑ p ( x ) log ( q ( x ) ) + ∑ p ( x ) log ( p ( x ) ) = H ( P , Q ) − H ( P ) KL(P||Q) = \sum p(x)\log \frac{p(x)}{q(x)} = -\sum p(x)\log(q(x)) + \sum p(x)\log(p(x)) = H(P,Q) - H(P) KL(P∣∣Q)=∑p(x)logq(x)p(x)=−∑p(x)log(q(x))+∑p(x)log(p(x))=H(P,Q)−H(P)
最后得到的第一项称作 P P P和 Q Q Q的交叉熵(cross entropy),后面一项就是熵。
在信息论中,熵代表着信息量, H ( P ) H(P) H(P)代表着基于 P P P分布自身的编码长度,也就是最优的编码长度(最小字节数)。而 H ( P , Q ) H(P,Q) H(P,Q)则代表着用 Q Q Q的分布去近似 P P P分布的信息,自然需要更多的编码长度。并且两个分布差异越大,需要的编码长度越大。所以两个值相减是大于等于0的一个值,代表冗余的编码长度,也就是两个分布差异的程度。所以KL散度在信息论中还可以称为相对熵(relative entropy)。
对深度学习中的生成模型来说,我们希望最小化真实数据分布与生成数据分布之间的KL散度,从而使得生成数据尽可能接近真实数据的分布。在实际场景中,我们是几乎不可能知道真实数据分布 P d a t a ( x ) P_{data}(x) Pdata(x)的,我们使用训练数据形成的生成分布在逼近 P d a t a ( x ) P_{data}(x) Pdata(x)。
【十】JS散度相关概念
JS散度全称Jensen-Shannon散度,简称JS散度。在概率统计中,JS散度也与KL散度一样具备了测量两个概率分布相似程度的能力,它的计算方法基于KL散度,继承了KL散度的非负性等,但有一点重要的不同,JS散度具备了对称性。
JS散度的公式如下所示,我们设定两个概率分布为 P P P和 Q Q Q,另外我们还设定 M = 0.5 × ( P + Q ) M = 0.5 \times (P + Q) M=0.5×(P+Q),KL为KL散度公式。
J S D ( P ∣ ∣ Q ) = 1 2 K L ( P ∣ ∣ M ) + 1 2 K L ( Q ∣ ∣ M ) JSD(P||Q) = \frac{1}{2}KL(P||M) + \frac{1}{2}KL(Q||M) JSD(P∣∣Q)=21KL(P∣∣M)+21KL(Q∣∣M)
如果我们把KL散度公式写入展开的话,结果如下所示:
J S D ( P ∣ ∣ Q ) = ∫ p ( x ) log p ( x ) p ( x ) + q ( x ) 2 d x + ∫ q ( x ) log q ( x ) p ( x ) + q ( x ) 2 d x JSD(P||Q) = \int p(x)\log \frac{p(x)}{\frac{p(x) +q(x)}{2}} dx+ \int q(x)\log \frac{q(x)}{\frac{p(x) +q(x)}{2}}dx JSD(P∣∣Q)=∫p(x)log2p(x)+q(x)p(x)dx+∫q(x)log2p(x)+q(x)q(x)dx
深度学习中使用KL散度和JS散度进行度量的时候存在一个问题:
如果两个分布 P P P, Q Q Q离得很远,完全没有重叠的时候,那么KL散度值是没有意义的,而JS散度值是一个常数 log 2 \log2 log2。这对以梯度下降为基础的深度学习算法有很大影响,这意味梯度为0,即梯度消失。
【十一】K-means算法逻辑?
K-means算法是一个实用的无监督聚类算法,其聚类逻辑依托欧式距离,当两个目标的距离越近,相似度越大。对于给定的样本集,按照样本之间的距离大小,将样本集划分为 K K K个簇。让簇内的点尽量紧密的连在一起,而让簇间的距离尽量的大。
K-means的主要算法步骤:
- 选择初始化的 k k k个样本作为初始聚类中心 D = { D 1 , D 2 , D 3 , . . . , D k } D = \{ D_{1}, D_{2}, D_{3}, ..., D_{k} \} D={D1,D2,D3,...,Dk}。
- 针对数据集中每个样本 x i x_{i} xi,计算它到 k k k个聚类中心的距离并将其分到距离最小的聚类中心所对应的类中.
- 针对每个类别 D j D_{j} Dj,重新计算它的聚类中心 D j = 1 ∣ c j ∣ ∑ x ∈ c j x D_{j} = \frac{1}{|c_{j}|}\sum_{x\in c_{j}}x Dj=∣cj∣1∑x∈cjx。(即属于该类的所有样本的质心);
- 重复上面2和3两步的操作,直到达到设定的中止条件(迭代次数、最小误差变化等)。
K-Means的主要优点:
- 原理简单,实现容易,收敛速度快。
- 聚类效果较优。
- 算法的可解释度比较强。
- 主要需要调参的参数仅仅是簇数k。
K-Means的主要缺点:
- K值需要人为设定,不好把握。
- 对初始的簇中心敏感,不同选取方式会得到不同结果。
- 对于不是凸的数据集比较难收敛。
- 如果各隐含类别的数据不平衡,比如各隐含类别的数据量严重失衡,或者各隐含类别的方差不同,则聚类效果不佳。
- 迭代结果只是局部最优。
- 对噪音和异常点比较的敏感。
【十二】K近邻算法逻辑?
K近邻(K-NN)算法计算不同数据特征值之间的距离进行分类。存在一个样本数据集合,也称作训练数据集,并且数据集中每个数据都存在标签,即我们知道每一个数据与所属分类的映射关系。接着输入没有标签的新数据后,在训练数据集中找到与该新数据最邻近的K个数据,然后提取这K个数据中占多数的标签作为新数据的标签(少数服从多数逻辑)。
K近邻算法的主要步骤:
- 计算新数据与各个训练数据之间的距离。
- 按照距离的递增关系进行排序。
- 选取距离最小的K个点。
- 确定前K个点所在类别的出现频率。
- 返回前K个点中出现频率最高的类别作为新数据的预测分类。
K近邻算法的结果很大程度取决于K的选择。其距离计算一般使用欧氏距离或曼哈顿距离等经典距离度量。
K近邻算法的主要优点:
- 理论成熟,思想简单,既可以用来做分类又可以做回归。
- 可以用于非线性分类。
- 对数据没有假设,准确度高,对异常点不敏感。
- 比较适用于数据量比较大的场景,而那些数据量比较小的场景采用K近邻算法算法比较容易产生误分类情况。
K近邻算法的主要缺点:
- 计算复杂性高;空间复杂性高。
- 样本不平衡的时候,对稀有类别的预测准确率低。
- 是慵懒散学习方法,基本上不学习,导致预测时速度比起逻辑回归之类的算法慢。
- 可解释性不强。
----【Python/C/C++知识】----
【一】Python中assert的作用?
Python中assert(断言)用于判断一个表达式,在表达式条件为 f a l s e false false的时候触发异常。
断言可以在条件不满足程序运行的情况下直接返回错误,而不必等待程序运行后出现崩溃的情况。
Rocky直接举一些例子:
>>> assert True
>>> assert False
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
AssertionError
>>> assert 1 == 1
>>> assert 1 == 2
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
AssertionError
>>> assert 1 != 2
【二】Python中互换变量有不用创建临时变量的方法吗?
在Python中,当我们想要互换两个变量的值或将列表中的两个值交换时,我们可以使用如下的格式进行,不需要创建临时变量:
x, y = y, x
这么做的原理是什么呢?
首先一般情况下Python是从左到右解析一个语句的,但在赋值操作的时候,因为是右值具有更高的计算优先级,所以需要从右向左解析。
对于上面的代码,它的执行顺序如下:
先计算右值 y , x y , x y,x(这里是简单的原值,但可能会有表达式或者函数调用的计算过程), 在内存中创建元组(tuple),存储 y , x y, x y,x分别对应的值;计算左边的标识符,元组被分别分配给左值,通过解包(unpacking),元组中第一个标示符对应的值 ( y ) (y) (y),分配给左边第一个标示符 ( x ) (x) (x),元组中第二个标示符对应的值 ( x ) (x) (x),分配给左边第二个标示符 ( y ) (y) (y),完成了 x x x和 y y y的值交换。
【三】Python中的主要数据结构都有哪些?
- 列表(list)
- 元组(tuple)
- 字典(dict)
- 集合(set)
【四】Python中的可变对象和不可变对象?
可变对象与不可变对象的区别在于对象本身是否可变。
可变对象:list(列表) dict(字典) set(集合)
不可变对象:tuple(元组) string(字符串) int(整型) float(浮点型) bool(布尔型)
【五】Python中的None代表什么?
None是一个特殊的常量,表示空值,其和False,0以及空字符串不同,它是一个特殊Python对象, None的类型是NoneType。
None和任何其他的数据类型比较返回False。
>>> None == 0
False
>>> None == ' '
False
>>> None == None
True
>>> None == False
False
我们可以将None复制给任何变量,也可以给None赋值。
【六】Python中 ∗ a r g s *args ∗args和 ∗ ∗ k w a r g s **kwargs ∗∗kwargs的区别?
∗ a r g s *args ∗args和 ∗ ∗ k w a r g s **kwargs ∗∗kwargs主要用于函数定义。我们可以将不定数量的参数传递给一个函数。
这里的不定的意思是:预先并不知道函数使用者会传递多少个参数, 所以在这个场景下使用这两个关键字。
∗ a r g s *args ∗args
∗ a r g s *args ∗args是用来发送一个非键值对的可变数量的参数列表给一个函数。
我们直接看一个例子:
def test_var_args(f_arg, *argv):
print("first normal arg:", f_arg)
for arg in argv:
print("another arg through *argv:", arg)
test_var_args('hello', 'python', 'ddd', 'test')
-----------------结果如下-----------------------
first normal arg: hello
another arg through *argv: python
another arg through *argv: ddd
another arg through *argv: test
∗ ∗ k w a r g s **kwargs ∗∗kwargs
∗ ∗ k w a r g s **kwargs ∗∗kwargs允许我们将不定长度的键值对, 作为参数传递给一个函数。如果我们想要在一个函数里处理带名字的参数, 我们可以使用 ∗ ∗ k w a r g s **kwargs ∗∗kwargs。
我们同样举一个例子:
def greet_me(**kwargs):
for key, value in kwargs.items():
print("{0} == {1}".format(key, value))
greet_me(name="yasoob")
-----------结果如下-------------
name == yasoob
【七】Python中Numpy的broadcasting机制?
Python的Numpy库是一个非常实用的数学计算库,其broadcasting机制给我们的矩阵运算带来了极大地方便。
我们先看下面的一个例子:
>>> import numpy as np
>>> a = np.array([1,2,3])
>>> a
array([1, 2, 3])
>>> b = np.array([6,6,6])
>>> b
array([6, 6, 6])
>>> c = a + b
>>> c
array([7, 8, 9])
上面的代码其实就是把数组 a a a和数组 b b b中同样位置的每对元素相加。这里 a a a和 b b b是相同长度的数组。
如果两个数组的长度不一致,这时候broadcasting就可以发挥作用了。
比如下面的代码:
>>> d = a + 5
>>> d
array([6, 7, 8])
broadcasting会把 5 5 5扩展成 [ 5 , 5 , 5 ] [5,5,5] [5,5,5],然后上面的代码就变成了对两个同样长度的数组相加。示意图如下(broadcasting不会分配额外的内存来存取被复制的数据,这里只是方面描述):

我们接下来看看多维数组的情况:
>>> e
array([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])
>>> e + a
array([[2., 3., 4.],
[2., 3., 4.],
[2., 3., 4.]])
在这里一维数组被扩展成了二维数组,和 e e e的尺寸相同。示意图如下所示:

我们再来看一个需要对两个数组都做broadcasting的例子:
>>> b = np.arange(3).reshape((3,1))
>>> b
array([[0],
[1],
[2]])
>>> b + a
array([[1, 2, 3],
[2, 3, 4],
[3, 4, 5]])
在这里 a a a和 b b b都被扩展成相同的尺寸的二维数组。示意图如下所示:

总结broadcasting的一些规则:
- 如果两个数组维数不相等,维数较低的数组的shape进行填充,直到和高维数组的维数匹配。
- 如果两个数组维数相同,但某些维度的长度不同,那么长度为1的维度会被扩展,和另一数组的同维度的长度匹配。
- 如果两个数组维数相同,但有任一维度的长度不同且不为1,则报错。
>>> a = np.arange(3)
>>> a
array([0, 1, 2])
>>> b = np.ones((2,3))
>>> b
array([[1., 1., 1.],
[1., 1., 1.]])
>>> a.shape
(3,)
>>> a + b
array([[1., 2., 3.],
[1., 2., 3.]])
接下来我们看看报错的例子:
>>> a = np.arange(3)
>>> a
array([0, 1, 2])
>>> b = np.ones((3,2))
>>> b
array([[1., 1.],
[1., 1.],
[1., 1.]])
>>> a + b
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: operands could not be broadcast together with shapes (3,) (3,2)
【八】Python中的实例方法、静态方法和类方法三者区别?
不用@classmethod和@staticmethod修饰的方法为实例方法。在类中定义的方法默认都是实例方法。实例方法最大的特点是它至少要包含一个self参数,用于绑定调用此方法的实例对象,实例方法通常可以用类对象直接调用。
采用@classmethod修饰的方法为类方法。类方法和实例方法相似,它至少也要包含一个参数,只不过类方法中通常将其命名为cls,Python会自动将类本身绑定给cls参数。我们在调用类方法时,无需显式为cls参数传参。
采用@staticmethod修饰的方法为静态方法。静态方法没有类似self、cls这样的特殊参数,因此Python的解释器不会对它包含的参数做任何类或对象的绑定。也正因为如此,类的静态方法中无法调用任何类属性和类方法。
【九】Python中常见的切片操作
[:n]代表列表中的第一项到第n项。我们看一个例子:
example = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
print(example[:6])
---------结果---------
[1, 2, 3, 4, 5, 6]
[n:]代表列表中第n+1项到最后一项:
example = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
print(example[6:])
---------结果---------
[7, 8, 9, 10]
[-1]代表取列表的最后一个元素:
example = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
print(example[-1])
---------结果---------
10
[:-1]代表取除了最后一个元素的所有元素:
example = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
print(example[:-1])
---------结果---------
[1, 2, 3, 4, 5, 6, 7, 8, 9]
[::-1]代表取整个列表的相反列表:
example = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
print(example[::-1])
---------结果---------
[10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
[1:]代表从第二个元素意指读取到最后一个元素:
example = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
print(example[1:])
---------结果---------
[2, 3, 4, 5, 6, 7, 8, 9, 10]
[4::-1]代表取下标为4(即第五个元素)的元素和之前的元素反转读取:
example = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
print(example[4::-1])
---------结果---------
[5, 4, 3, 2, 1]
【十】Python中如何进行异常处理?
一般情况下,在Python无法正常处理程序时就会发生一个异常。异常在Python中是一个对象,表示一个错误。当Python脚本发生异常时我们需要捕获处理它,否则程序会终止执行。
捕捉异常可以使用try,except和finally语句。
try和except语句用来检测try语句块中的错误,从而让except语句捕获异常信息并处理。
try:
6688 / 0
except:
'''异常的父类,可以捕获所有的异常'''
print "0不能被除"
else:
'''保护不抛出异常的代码'''
print "没有异常"
finally:
print "最后总是要执行我"
【十一】Python中remove,del以及pop之间的区别?
remove,del以及pop都可以用于删除列表、字符串等里面的元素,但是具体用法并不相同。
- remove是剔除第一个匹配的值。
- del是通过索引来删除当中的元素。
- pop是通过索引来删除当中的元素,并且返回该元素;若括号内不添加索引值,则默认删除最后一个元素。
>>> a = [0, 1, 2, 1, 3]
>>> a.remove(1)
>>> a
[0, 2, 1, 3]
>>> a = [0, 1, 2, 1, 3]
>>> del a[1]
[0, 2, 1, 3]
>>> a = [0, 1, 2, 1, 3]
>>> a.pop(1)
1
>>> a
[0, 2, 1, 3]
【十二】C/C++中野指针的概念?
野指针也叫空悬指针,不是指向null的指针,是未初始化或者未清零的指针。
产生原因:
-
指针变量未及时初始化。
-
指针free或delete之后没有及时置空。
解决办法:
-
定义指针变量及时初始化活着置空。
-
释放操作后立即置空。
【十三】C/C++中内存泄漏以及解决方法?
内存泄漏是指己动态分配的堆内存由于某种原因导致程序未释放或无法释放,造成系统内存的浪费,导致程序运行速度减慢甚至系统崩溃等严重后果。
解决方法:
造成内存泄漏的主要原因是在使用new或malloc动态分配堆上的内存空间,而并未使用delete或free及时释放掉内存造成的。所以解决方法就是注意new/delete和malloc/free一定要配套使用。
【十四】C/C++中面向对象和面向过程的区别?
面向对象(Object Oriented Programming,OOP)编程模型首先抽象出各种对象(各种类),并专注于对象与对象之间的交互,对象涉及的方法和属性都封装在对象内部。
面向对象的编程思想是一种依赖于类和对象概念的编程方式,一个形象的例子是将大象装进冰箱:
- 冰箱是一个对象,大象也是一个对象。
- 冰箱有自己的方法,打开、存储、关闭等;大象也有自己的方法,吃、走路等。
- 冰箱有自己的属性:长、宽、高等;大象也有自己的属性:体重、高度、体积等。
面向过程(Procedure Oriented Programming,POP)编程模型是将问题分解成若干步骤(动作),每个步骤(动作)用一个函数来实现,在使用的时候,将数据传递给这些函数。
面向过程的编程思想通常采用自上而下、顺序执行的方式进行,一个形象的例子依旧是将大象装进冰箱:
- 打开冰箱。
- 把大象装进冰箱。
- 关闭冰箱。
面向对象和面向过程的区别:
-
安全性角度。面向对象比面向过程安全性更高,面向对象将数据访问隐藏在了类的成员函数中,而且类的成员变量和成员函数都有不同的访问属性;而面向过程并没有办法来隐藏程序数据。
-
程序设计角度。面向过程通常将程序分为一个个的函数;而面向对象编程中通常使用一个个对象,函数通常是对象的一个方法。
-
逻辑过程角度。面向过程通常采用自上而下的方法;而面向对象通常采用自下而上的方法。
-
程序扩展性角度。面向对象编程更容易修改程序,更容易添加新功能。
【十五】C/C++中常用容器功能汇总
vector(数组)
vector是封装动态数组的顺序容器。
成员函数:
- at():所需元素值的引用。
- front():访问第一个元素(返回引用)。
- back():访问最后一个元素(返回引用)。
- beign():返回指向容器第一个元素的迭代器。
- end():返回指向容器末尾段的迭代器。
- empty():检查容器是否为空。
- size():返回容器中的元素数。
- capacity():返回当前存储空间能够容纳的元素数。
- clear():清除内容。
- insert():插入元素。
- erase():擦除元素。
- push_back():将元素添加到容器末尾。
- pop_back():移除末尾元素。
- *max_element(v.begin(), v.end()):返回数组最大值。
- *min_element(v.begin(), v.end()):返回数组最小值。
queue(队列)
queue是容器适配器,他是FIFO(先进先出)的数据结构。
成员函数:
- front():访问第一个元素(返回引用)。
- back():访问最后一个元素(返回引用)。
- empty():检查容器是否为空。
- size():返回容器中的元素数。
- push():向队列尾部插入元素。
- pop():删除首个元素。
deque(双端队列)
deque是有下标顺序容器,它允许在其首尾两段快速插入和删除。
成员函数:
- front():访问第一个元素(返回引用)。
- back():访问最后一个元素(返回引用)。
- beign():返回指向容器第一个元素的迭代器。
- end():返回指向容器末尾段的迭代器。
- empty():检查容器是否为空。
- size():返回容器中的元素数。
- clear(): 清除内容。
- insert():插入元素。
- erase():擦除元素。
- push_back():将元素添加到容器末尾。
- pop_back():移除末尾元素。
- push_front():插入元素到容器起始位置。
- pop_front():移除首元素。
- at():所需元素值的引用。
set(集合)
集合基于红黑树实现,有自动排序的功能,并且不能存放重复的元素。
成员函数:
-
begin()–返回指向第一个元素的迭代器。
-
clear()–清除所有元素。
-
count()–返回某个值元素的个数。
-
empty()–如果集合为空,返回true。
-
end()–返回指向最后一个元素的迭代器。
-
erase()–删除集合中的元素。
-
find()–返回一个指向被查找到元素的迭代器。
-
insert()–在集合中插入元素。
-
size()–集合中元素的数目。
unordered_set(无序集合)
无序集合基于哈希表实现,不能存放重复的元素。元素类型必须可以比较是否相等,因为这可以确定元素什么时候相等。
成员函数:
- empty():检查容器是否为空。
- size():返回容器中的元素数。
- insert():插入元素。
- clear():清除内容。
- count():返回匹配特定键的元素数量。
- find():寻找带有特定键的元素。
- erase()–删除集合中的元素。
unordered_map
unordered_map是关联容器,含有带唯一键的键-值对。
搜索、插入和元素移除拥有平均常数时间复杂度。
元素在内部不以任何特定顺序排序,而是组织进桶中。元素放进哪个桶完全依赖于其键的哈希。这允许对单独元素的快速访问,因为一旦计算哈希,则它准确指代元素所放进的桶。
成员函数:
- empty():检查容器是否为空。
- size():返回可容纳的元素数。
- insert():插入元素。
- clear():清除内容。
- count():返回匹配特定键的元素数量。
- find():寻找带有特定键的元素。
- erase()–删除集合中的元素。
【十六】C/C++中指针和引用的区别
C语言的指针让我们拥有了直接操控内存的强大能力,而C++在指针基础上又给我们提供了另外一个强力武器 → \to →引用。
首先我们来看一下C++中对象的定义:对象是指一块能存储数据并具有某种类型的内存空间。
一个对象a,它有值和地址&a。运行程序时,计算机会为该对象分配存储空间,来存储该对象的值,我们通过该对象的地址,来访问存储空间中的值。
指针p也是对象,它同样有地址&p和存储的值p,只不过,p存储的是其他对象的地址。如果我们要以p中存储的数据为地址,来访问对象的值,则要在p前加引用操作符 ∗ * ∗,即 ∗ p *p ∗p。
对象有常量(const)和变量之分,既然指针本身是对象,那么指针所存储的地址也有常量和变量之分,指针常量是指,指针这个对象所存储的地址是不可改变的,而常量指针的意思就是指向常量的指针。
我们可以把引用理解成变量的别名。定义一个引用的时候,程序把该引用和它的初始值绑定在一起,而不是拷贝它。计算机必须在声明引用r的同时就要对它初始化,并且r一经声明,就不可以再和其他对象绑定在一起了。
实际上,我们也可以把引用看作是通过一个指针常量来实现的,指向的地址不变,地址里的内容可以改变。
接下来我们来看看指针和引用的具体区别:
- 指针是一个新的变量,要占用存储空间,存储了另一个变量的地址,我们可以通过访问这个地址来修改另一个变量。而引用只是一个别名,还是变量本身,不占用具体存储空间,只有声明没有定义。对引用的任何操作就是对变量本身进行操作,以达到修改变量的目的。
- 引用只有一级,而指针可以有多级。
- 指针传参的时候,还是值传递,指针本身的值不可以修改,需要通过解引用才能对指向的对象进行操作。引用传参的时候,传进来的就是变量本身,因此变量可以被修改。
- 引用它一定不为空,因此相对于指针,它不用检查它所指对象是否为空,这样就提高了效率。
- 引用必须初始化,而指针可以不初始化。
我们可以看下面的代码:
int a,b,*p,&r=a;//正确
r=3;//正确:等价于a=3
int &rr;//出错:引用必须初始化
p=&a;//正确:p中存储a的地址,即p指向a
*p=4;//正确:p中存的是a的地址,对a所对应的存储空间存入值4
p=&b//正确:p可以多次赋值,p存储b的地址
“&”不仅能表示引用,还可以表示成地址,还有可以作为按位与运算符。这个要根据具体情况而定。比如上面的例子,等号左边的,被解释为引用,右边的被解释成取地址。
引用的操作加了比指针更多的限制条件,保证了整体代码的安全性和便捷性。引用的合理使用可以一定程度避免“指针满天飞”的情况,可以一定程度上提升程序鲁棒性。并且指针与引用底层实现都是一样的,不用担心两者的性能差距。
【十七】C/C++中宏定义的相关知识
宏定义可以把一个名称指定成任何一个文本。在完成宏定义后,无论宏名称出现在源代码的何处,预处理器都会将其替换成指定的文本。
//define 宏名 文本
#define WeThinkIn 666688889999
//define 宏名(参数) 文本
#define R(a,b) (a/b)
//注:带参数的宏替换最好在表达式整体上加括号,避免结果受其他运算影响。
宏定义的优点:
- 方便程序修改,如果一个常量在程序中大量使用,我们可以使用宏定义为其设置一个标识符。当我们想修改这个常量时,直接修改宏定义处即可,不必在程序中海量寻找所有相关位置。
- 提高程序的运行效率,使用带参数的宏定义可以完成函数的功能,但同时又比函数节省系统开销,提升程序运行效率。(无需调用函数这个流程)
宏定义和函数的区别:
- 宏在预处理阶段完成替换,之后替换的文本参与编译,相当于是恒等代换过程,运行时不存在函数调用,执行起来更快;而函数调用在运行时需要跳转到具体调用函数。
- 宏定义没有返回值;函数调用具有返回值。
- 宏定义参数没有类型,不进行类型检查;函数参数具有类型,需要检查类型。
- 宏定义不是说明或者语句,结尾不用加分号。
- 宏定义必须写在函数之外,其作用域为宏定义命令起到源程序结束。如要终止其作用域可使用# undef命令;而函数作用域在函数调用处。
【十八】C/C++中typedef关键字的相关知识
我们可以使用typedef关键字来定义自己习惯的数据类型名称,来替代系统默认的基本类型名称以及其他类型等名称。
在工业界中,我们一般在如下两个场景中会见到typedef的身影。
// 1.为基本数据类型定义新的类型名
typedef unsigned int WeThinkIn_int;
typedef char* WeThinkIn_point;
// 2.为自定义数据类型(结构体、共用体和枚举类型)定义简洁的类型名称
typedef struct target_Object
{
int x;
int y;
} WeThinkIn_Object;
typedef与宏定义的区别:
- 宏主要用于定义常量及书写复杂的内容;typedef主要用于定义类型别名。
- 宏替换发生在预处理阶段,属于文本恒等替换;typedef是编译中发挥作用。
- 宏定义参数没有类型,不进行类型检查;typedef参数具有类型,需要检查类型。
- 宏不是语句,不用在最后加分号;typedef是语句,要加分号标识结束。
- 注意对指针的操作,typedef char * p_char和#define p_char char *区别巨大。
----【模型部署】----
【一】什么是异构计算?
首先,异构现象是指不同计算平台之间,由于硬件结构(包括计算核心和内存),指令集和底层软件实现等方面的不同而有着不同的特性。
异构计算是指联合使用两个或者多个不同的计算平台,并进行协同运算。比如CPU和GPU的异构计算,TPU和GPU的异构计算以及TPU/GPU/CPU的异构计算等等。
【二】端侧部署时整个解决方案的核心指标?
- 精度
- 耗时
- 内存占用
- 功耗
【三】什么是模型量化?
通常的深度学习模型参数是FP32浮点型的,而模型量化主要是使用FP16,INT8以及INT4等低精度类型来保存模型参数,从而有效的降低模型计算量和内存占用,并将精度损失限制在一个可接受的范围内。
模型量化主要分在线量化和离线量化。在线量化在模型训练阶段采用量化方法进行量化。离线量化主要在模型离线工具(模型转换阶段)中采用量化方法进行量化。
工业界中主要使用离线量化作为通用模型量化的解决方案。
【四】什么是模型剪枝?
模型剪枝按照剪枝粒度可分为突触剪枝、神经元剪枝、权重矩阵剪枝等,主要是将权重矩阵中不重要的参数设置为0,结合稀疏矩阵来进行存储和计算。通常为了保证性能,需要逐步进行迭代剪枝,让精度损失限制在一个可接受的范围。
突触剪枝剪掉神经元之间的不重要的连接。对应到权重矩阵中,相当于将某个参数设置为0。
神经元剪枝则直接将某个节点直接裁剪。对应到权重矩阵中,相当于某一行和某一列置零。
除此之外,也可以将整个权重矩阵裁剪,每一层中只保留最重要的部分,这就是权重矩阵剪枝。相比突触剪枝和神经元剪枝,权重矩阵剪枝压缩率要大很多。
【五】主流AI端侧硬件平台有哪些?
- 英伟达
- 海思
- 寒武纪
- 比特大陆
- 昇腾
- 登临
- 联咏
- 安霸
- 耐能
- 爱芯
- 瑞芯
【六】主流AI端侧硬件平台一般包含哪些模块?
- 视频编解码模块
- CPU核心处理模块
- AI协处理器模块
- GPU模块
- DSP模块
- DDR内存模块
- 数字图像处理模块
【七】算法工程师该如何看待硬件侧知识?
GPU乃至硬件侧的整体逻辑,是CV算法工作中必不可少的组成部分,也是算法模型所依赖的重要物理载体。
GPU的相关知识
现在AI行业有个共识,认为是数据的爆发和算力的突破开启了深度学习在计算机视觉领域的“乘风破浪”,而其中的算力,主要就是指以GPU为首的计算平台。
GPU(Graphical Processing Unit)从最初用来进行图形处理和渲染(玩游戏),到通过CUDA/OpenCL库以及相应的工程开发之后,成为深度学习模型在学术界和工业界的底层计算工具,其有以下的一些特征:
- 异构计算:GPU能作为CPU的协处理器与CPU协同运算。
- 单指令流多数据流(SIMD)架构:使得同一个指令(比如对图像数据的一些操作),可以同时在多个像素点上并行计算,从而得到比较大的吞吐量,深度学习中大量的矩阵操作,让GPU成为一个非常适合的计算平台。
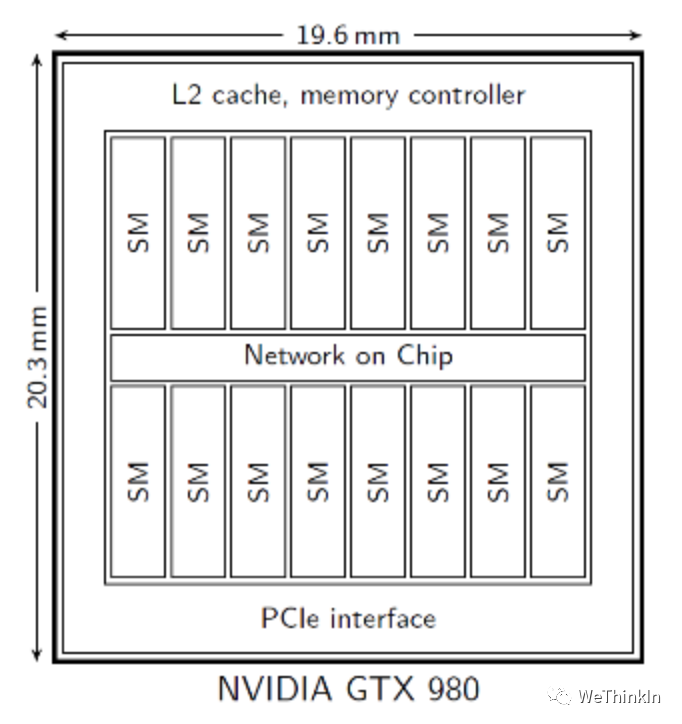
- 多计算核心。比如Nvidia的GTX980GPU中,在和i7-5960CPU差不多的芯片面积上,有其128倍的运算速度。GTX980中有16个流处理单元,每个流处理单元中包含着128个CUDA计算核心,共有2048个GPU运算单元,与此同时i7-5960CPU只有16个类似的计算单元。
- CUDA模块。作为GPU架构中的最小单元,它的设计和CPU有着非常类似的结构,其中包括了一个浮点运算单元,整型运算单元以及控制单元。一个流处理单元中的CUDA模块将执行同一个指令,但是会作用在不同的数据上。多CUDA模块意味着GPU有更加高的计算性能,但更重要的是在算法侧有没有高效地调度和使用。
- 计算核心频率。即时钟频率,代表每一秒内能进行同步脉冲次数。就核心频率而言,CPU要高于GPU。由于GPU采用了多核逻辑,即使提高一些频率,其实对于总体性能影响不会特别大。
- 内存架构。GPU的多层内存架构包括全局内存,2级缓存,和芯片上的存储(包括寄存器,和1级缓存共用的共享内存,只读/纹理缓存和常量缓存)。
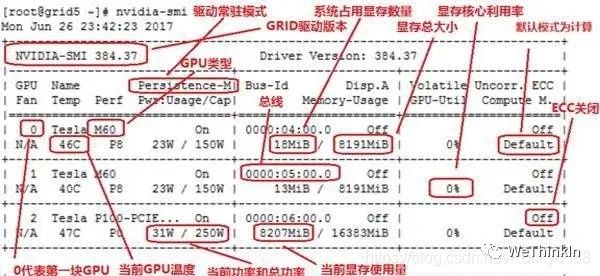
在使用GPU时,在命令行输入nvidia-smi命令时会打印出一张表格,其中包含了GPU当时状态的所有参数信息。
CUDA/cuDNN/OpenCL科普小知识:
- CUDA是NVIDIA推出的用于GPU的并行计算框架。
- cuDNN是NVIDIA打造的针对深度神经网络的加速库,是一个用于深层神经网络的GPU加速库。
- OpenCL是由苹果(Apple)公司发起,业界众多著名厂商共同制作的面向异构系统通用目的并行编程的开放式、免费标准,也是一个统一的编程环境。
深度学习的端侧设备
深度学习的端侧设备,又可以叫做边缘计算设备,深度学习特别是CV领域中,模型+端侧设备的组合能够加快业务的即时计算,决策和反馈能力,极大释放AI可能性。

深度学习的端侧设备主要由ARM架构的CPU+ GPU/TPU/NPU等协处理器 + 整体功耗 + 外围接口 + 工具链等部分组成,也是算法侧对端侧设备进行选型要考虑的维度。
在实际业务中,根据公司的不同,算法工程师涉及到的硬件侧范围也会不一样。如果公司里硬件和算法由两个部门分别负责,那么算法工程师最多接触到的硬件侧知识就是硬件性能评估,模型转换与模型硬件侧验证,一些硬件高层API接口的开发与使用;如果公司里没有这么细分的部门,那么算法工程师可能就会接触到端侧的视频编解码,模型推理加速,Opencv,FFmpeg,Tensor RT,工具链开发等角度的知识。

算法工程师该如何看待硬件侧
首先,整体上还是要将硬件侧工具化,把端侧设备当做算法模型的一个下游载体,会熟练的选型与性能评估更加重要。
端侧设备是算法产品整体解决方案中一个非常重要的模块,算法+硬件的范式将在未来的边缘计算与万物智能场景中持续发力。
在日常业务中,算法模型与端侧设备的适配性与兼容性是必须要考虑的问题,端侧设备是否兼容一些特殊的网络结构?算法模型转化并部署后,精度是否下降?功耗与耗时能否达标?等等都让算法工程师的模型设计逻辑有更多的抓手。
【八】现有的一些移动端开源框架?
- NCNN,其GitHub地址:https://github.com/Tencent/ncnn
- Paddle Lite,其GitHub地址:https://github.com/PaddlePaddle/paddle-mobile
- MACE( Mobile AI Compute Engine),其GitHub地址:https://github.com/XiaoMi/mace
- TensorFlow Lite,其官网地址:https://www.tensorflow.org/lite?hl=zh-cn
- PocketFlow,其GitHub地址:https://github.com/Tencent/PocketFlow
- 等等。。。
【九】端侧静态多Batch和动态多Batch的区别
当设置静态多Batch后,如Batch=6,那么之后不管是输入2Batch还是4Batch,都会按照6Batch的预设开始申请资源。
而动态多Batch不用预设Batch数,会根据实际场景中的真实输入Batch数来优化资源的申请,提高端侧实际效率。
由于动态多Batch的高性能,通常Inference耗时和内存占用会比静态多Batch时要大。
【十】优化模型端侧性能的一些方法
- 设计能最大限度挖掘AI协处理器性能的模型结构。
- 多模型共享计算内存。
- 减少模型分支结构,减少模型元素级操作。
- 卷积层的输入和输出特征通道数相等时MAC最小,以提升模型Inference速度。
【十一】ONNX的相关知识
ONNX是一种神经网络模型的框架,其最经典的作用是作为不同框架之间的中间件,成为模型表达的一个通用架构,来增加不同框架之间的交互性。
ONNX的优势:
- ONNX的模型格式有极佳的细粒度。
- ONNX是模型表达的一个通用架构,主流框架都可以兼容。
- ONNX可以实现不同框架之间的互相转化。
【十二】TensorRT的相关知识
TensorRT是一个高性能的深度学习前向Inference的优化器和运行的引擎。
TensorRT的核心:将现有的模型编译成一个engine,类似于C++的编译过程。在编译engine过程中,会为每一层的计算操作找寻最优的算子方法,将模型结构和参数以及相应kernel计算方法都编译成一个二进制engine,因此在部署之后大大加快了推理速度。
我们需要给TensorRT填充模型结构和参数,也就是解析我们自己的模型结构和参数文件,获取数据放到其中。官方给了三种主流框架模型格式的解析器(parser),分别是:ONNX,Caffe以及TensorFlow。
TensorRT的优势:
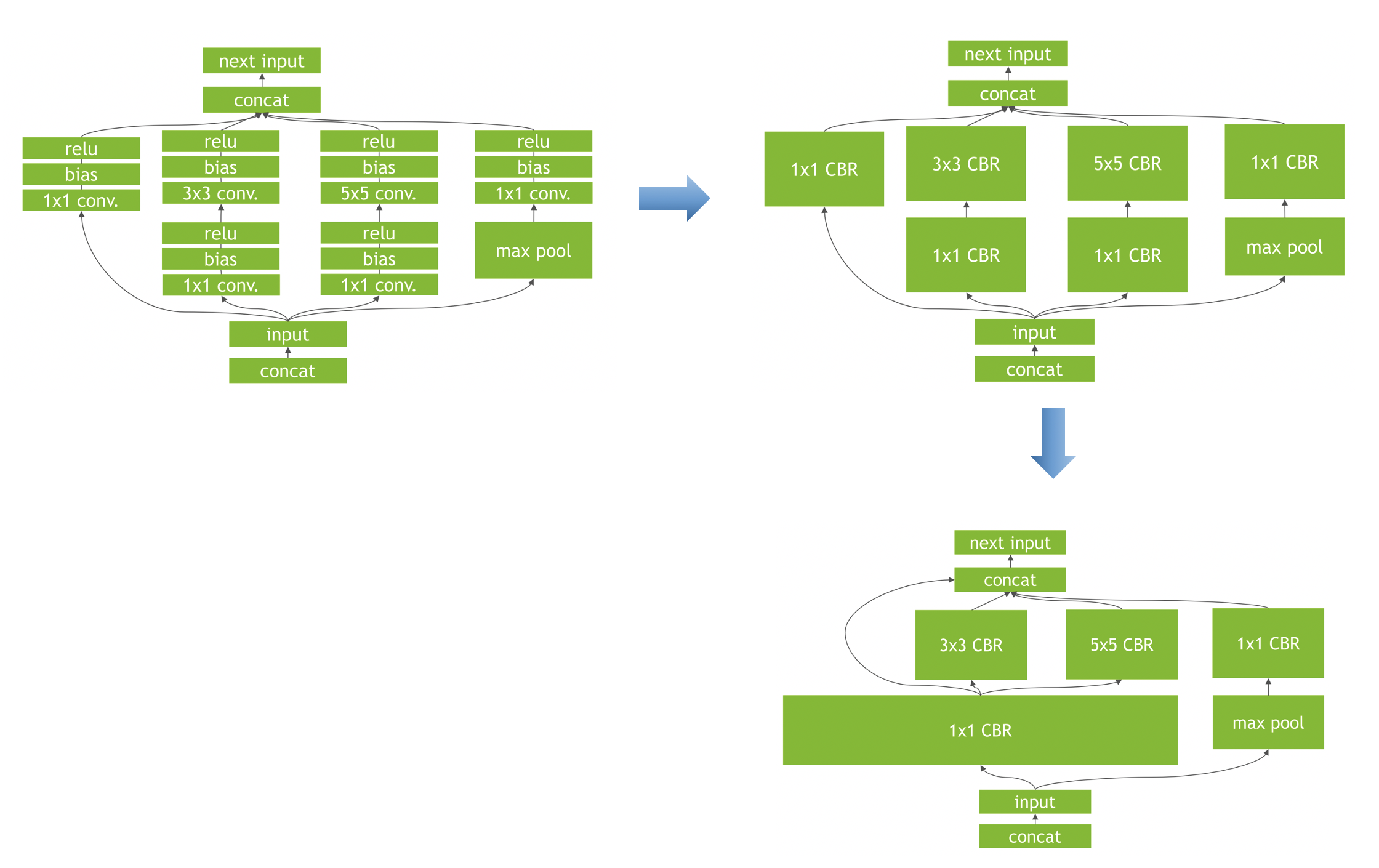
- 把一些网络层进行了合并。具体🌰如下图所示。
- 取消一些不必要的操作。比如不用专门做concat的操作等。
- TensorRT会针对不同的硬件都相应的优化,得到优化后的engine。
- TensorRT支持INT8和FP16的计算,通过在减少计算量和保持精度之间达到一个理想的trade-off。
----【图像处理基础】----
【一】有哪些常用的图像质量评价指标?
- 峰值信噪比(Peak-Signal to Noise Ratio,PSNR)
- 均方误差(Mean Square Error,MSE)
- MAE(Mean Absolute Error,MSE)
- 信噪比SNR(Signal to Noise Ratio,SNR)
- 信息保真度准则(Information Fidelity Criterion,IFC)
- 视觉信息保真度(Visual Information Fidelity,VIF)
- 结构相似度(Structure Similaruty,SSIM)
【二】什么是图像畸变?
使用摄像头时,可能会出现图像边缘线条弯曲的情况,尤其是边缘部分是直线时,这种现象更为明显。比如摄像头显示画面中的门框、电线杆、墙面棱角、吊顶线等出现在边缘时,可能会有比较明显的弯曲现象,这种现象就叫做畸变。
畸变是指光学系统对物体所成的像相对于物体本身而言的失真程度,是光学透镜的固有特性,其直接原因是因为镜头的边缘部分和中心部分的放大倍率不一样导致。畸变并不影响像的清晰程度,只改变物体的成像形状,畸变是一种普遍存在的光学现象。

【三】RGB图像转为灰度图的方法?
- RGB任选一通道作为灰度图
- RGB中最大值最为灰度图
- RGB的均值作为灰度图
- RGB的加权均值作为灰度图
【四】仿射变换和透视变换的概念?
仿射变换是对图片进行平移,缩放,倾斜和旋转等操作,是一种二维坐标到二维坐标之间的线性变换。它保持了二维图形的“平直性”(直线经过变换之后依然是直线)和“平行性”(二维图形之间的相对位置关系保持不变,平行线依然是平行线,且直线上点的位置顺序不变)。
透视变换是将图片投影到一个新的视平面,也称作投影映射。它是将二维图片投影到三维空间,再投回另一个二维空间的映射操作。
仿射变换和透视变换的最大区别:一个平行四边形,经过仿射变换后依然是平行四边形;而经过透视变换后只是一个四边形(不再平行了)。
【五】图像噪声的种类?
常规噪声
- 高斯噪声
- 脉冲噪声
- 泊松噪声
- 乘性噪声
- 瑞利噪声
- 伽马噪声
- 指数噪声
- 均匀噪声
- 椒盐噪声
- 散粒噪声
- 泊松噪声
对抗噪声
- 白盒对抗噪声
- 黑盒查询对抗噪声
- 黑盒迁移噪声
- 物理对抗噪声
【六】Python中OpenCV和PIL的区别?
- 在读取图片时,OpenCV按照BGR的色彩模式渲染通道,而PIL按照RGB的色彩模式渲染通道。
- OpenCV性能较优,可以作为算法与工程的必备模块。
【七】有哪些常用的图像去噪算法?
- 空间域去燥:均值滤波器,中值滤波器,低通滤波器,高斯滤波,双边滤波,引导滤波,NLM(Non-Local means)算法等。
- 频域去燥:小波变换,傅里叶变换,离散余弦变换,形态学滤波等。
【八】有哪些常用的图像频域信息分离方法?
可以使用频域滤波器如小波变换,傅里叶变换,余弦变换,形态学滤波等方法将图像高低频信息分离。
【九】有哪些常用一阶微分梯度算子?
梯度算子
想要得到一张图像的梯度,要在图像的每个像素点处计算偏导数。因此一张图像 f f f在 ( x , y ) (x,y) (x,y)位置处的 x x x和 y y y方向上的梯度大小 g x g_{x} gx和 g y g_{y} gy分别计算为:
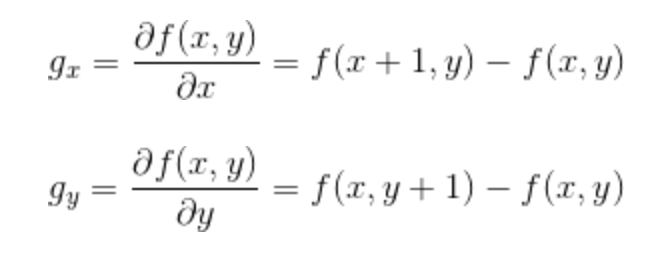
上述两个公式对所有的 x x x和 y y y的计算值可用下面的一维模版对 f ( x , y ) f(x,y) f(x,y)的滤波得到。
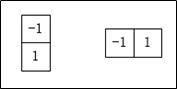
用于计算梯度偏导数的滤波器模版,通常称之为梯度算子、边缘算子和边缘检测子等。
经典一阶梯度算子
Roberts算子
Roberts算子又称为交叉微分算法,它是基于交叉差分的梯度算法,通过局部差分计算检测边缘线条。常用来处理具有陡峭的低噪声图像,当图像边缘接近于正45度或负45度时,该算法处理效果更理想。其缺点是对边缘的定位不太准确,提取的边缘线条较粗。
Roberts算子的模板分为水平方向和垂直方向,如下式所示,从其模板可以看出,Roberts算子能较好的增强正负45度的图像边缘。
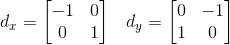
例如,下面给出Roberts算子的模板,在像素点 P 5 P5 P5处 x x x和 y y y方向上的梯度大小 g x g_{x} gx和 g y g_{y} gy分别计算为:


下图是Roberts算子的运行结果:

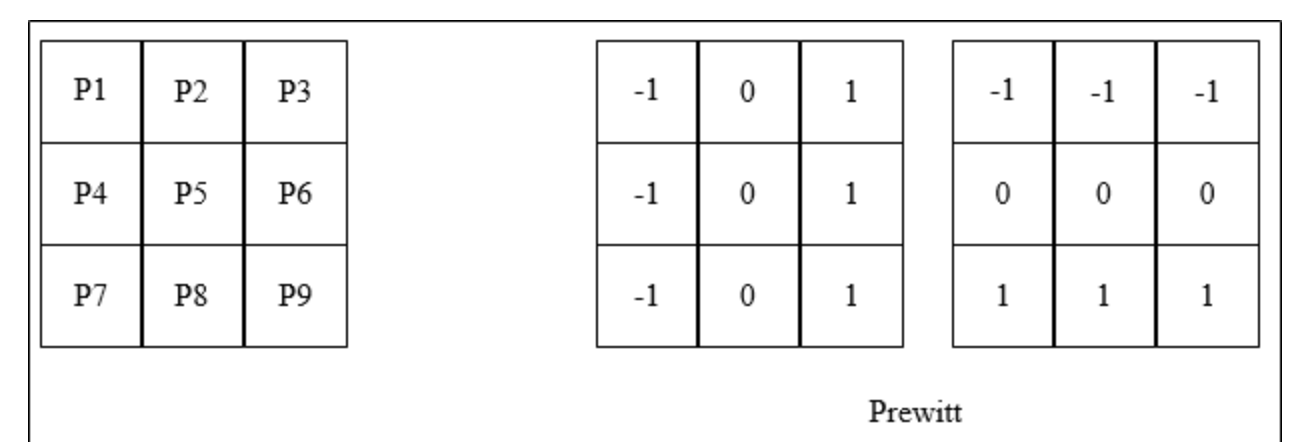
Prewitt算子
Prewitt算子是一种图像边缘检测的微分算子,其原理是利用特定区域内像素灰度值产生的差分实现边缘检测。由于Prewitt算子采用 3 × 3 3\times3 3×3卷积模板对区域内的像素值进行计算,而Robert算子的模板为 2 × 2 2\times2 2×2,故Prewitt算子的边缘检测结果在水平方向和垂直方向均比Robert算子更加明显。Prewitt算子适合用来识别噪声较多、灰度渐变的图像,其计算公式如下所示:

例如,下面给出Prewitt算子的模板,在像素点 P 5 P5 P5处 x x x和 y y y方向上的梯度大小 g x g_{x} gx和 g y g_{y} gy分别计算为:
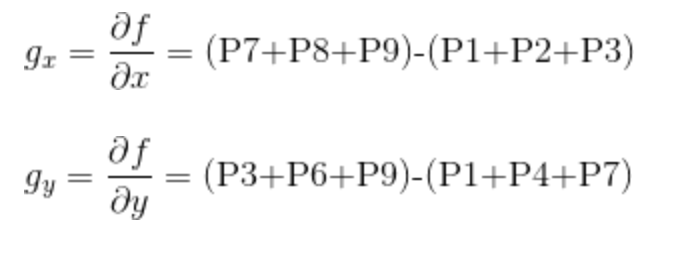
Prewitt算子运行结果如下:

Sobel算子
Sobel算子是一种用于边缘检测的离散微分算子,它结合了高斯平滑和微分求导。该算子用于计算图像明暗程度近似值,根据图像边缘旁边明暗程度把该区域内超过某个数的特定点记为边缘。Sobel算子在Prewitt算子的基础上增加了权重的概念,认为相邻点的距离远近对当前像素点的影响是不同的,距离越近的像素点对应当前像素的影响越大,从而实现图像锐化并突出边缘轮廓。
Sobel算子根据像素点上下、左右邻点灰度加权差,在边缘处达到极值这一现象检测边缘。对噪声具有平滑作用,提供较为精确的边缘方向信息。因为Sobel算子结合了高斯平滑和微分求导(分化),因此结果会具有更多的抗噪性,当对精度要求不是很高时,Sobel算子是一种较为常用的边缘检测方法。
Sobel算子的边缘定位更准确,常用于噪声较多、灰度渐变的图像。其算法模板如下面的公式所示,其中 d x d_{x} dx表示水平方向, d y d_{y} dy表示垂直方向。
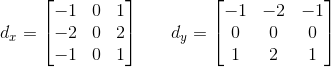
例如,下面给出Sobel算子的模板,在像素点 P 5 P5 P5处 x x x和 y y y方向上的梯度大小 g x g_{x} gx和 g y g_{y} gy分别计算为:

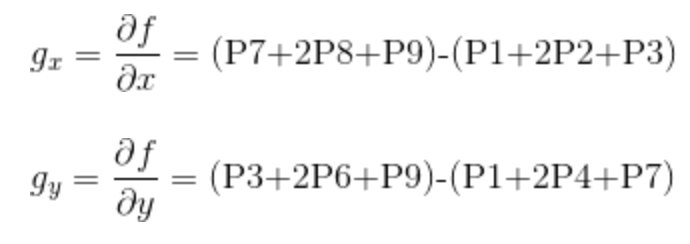
sobel算子的效果如下:

各类算子的优缺点
Roberts算子
Roberts算子利用局部差分算子寻找边缘,边缘定位精度较高,但容易丢失一部分边缘,不具备抑制噪声的能力。该算子对具有陡峭边缘且含噪声少的图像效果较好,尤其是边缘正负45度较多的图像,但定位准确率较差。
Sobel算子
Sobel算子考虑了综合因素,对噪声较多的图像处理效果更好,Sobel 算子边缘定位效果不错,但检测出的边缘容易出现多像素宽度。
Prewitt算子
Prewitt算子对灰度渐变的图像边缘提取效果较好,而没有考虑相邻点的距离远近对当前像素点的影响,与Sobel 算子类似,不同的是在平滑部分的权重大小有些差异。
【十】拉普拉斯算子的相关概念
拉普拉斯算子是一个二阶算子,比起一阶微分算子,二阶微分算子的边缘定位能力更强,锐化效果更好。
使用二阶微分算子的基本方法是定义一种二阶微分的离散形式,然后根据这个形式生成一个滤波模版,与图像进行卷积。
滤波器分各向同性滤波器和各向异性滤波器。各向同性滤波器与图像进行卷积时,图像旋转后响应不变,说明滤波器模版自身是对称的。如果是各向异性滤波器,当原图旋转90度时,原图某一点能检测出细节(突变)的,但是现在却检测不出来了,这说明滤波器不是对称的。由于拉普拉斯算子是最简单的各向同性微分算子,它具有旋转不变形。
对于二维图像 f ( x , y ) f(x,y) f(x,y),二阶微分最简单的定义(拉普拉斯算子定义):
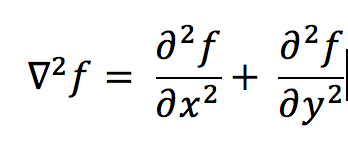
对于任意阶微分算子都是线性算子,所以二阶微分算子和后面的一阶微分算子都可以用生成模版然后卷积的方式得出结果。
根据前面对二阶微分的定义有:

根据上面的定义,与拉普拉斯算子的定义相结合,我们可以得到:
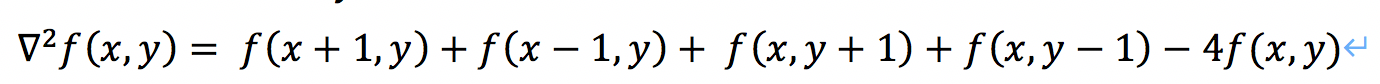
也就是一个点的拉普拉斯的算子计算结果是上下左右的灰度和减去本身灰度的四倍。同样,可以根据二阶微分的不同定义,所有符号相反,也就是上式所有灰度值全加上负号,就是-1,-1,-1,-1,4。但是我们要注意,符号改变,锐化的时候与原图的加或减应当相对变化。上面是四临接的拉普拉斯算子,将这个算子旋转45度后与原算子相架,就变成了八邻域的算子了,也就是一个像素周围一圈8个像素的和与中间像素8倍的差,作为拉普拉斯计算结果。
因为要强调图像中突变(细节),所以平滑灰度的区域,无响应,即模版系数的和为0,也是二阶微分的必备条件。
最后的锐化公式:
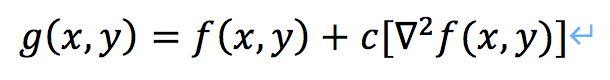
其中, g g g是输出, f f f为原始图像, c c c是系数,用来对细节添加的多少进行调节。
我们接下来用更加形象的图像来解释拉普拉斯算子的有效性。
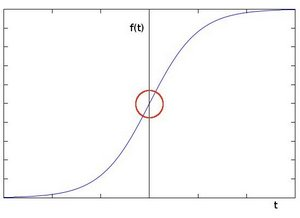
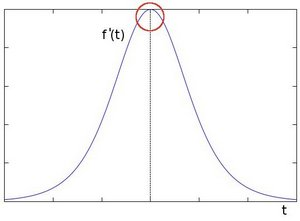
在边缘部分,像素值出现”跳跃“或者较大的变化。下图(a)中灰度值的”跃升”表示边缘的存在。如果使用一阶微分求导我们可以更加清晰的看到边缘”跃升”的存在(这里显示为高峰值)图(b)。
如果在边缘部分求二阶导数会出现什么情况呢,图©所示。
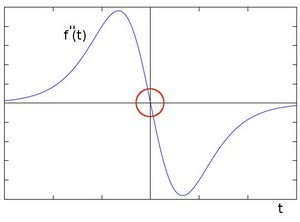
我们会发现在一阶导数的极值位置,二阶导数为0。所以我们也可以用这个特点来作为检测图像边缘的方法。但是,二阶导数的0值不仅仅出现在边缘(它们也可能出现在无意义的位置),但是我们可以过滤掉这些点。
为了更适合于数字图像处理,我们如上面的式子所示,将其表示成了离散形式。为了更好的进行变成,我们也可以将其表示成模版的形式:
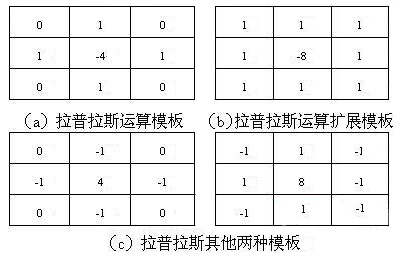
上图(a)表示离散拉普阿拉斯算子的模版,(b)表示其扩展模版,(c)则分别表示其他两种拉普拉斯的实现模版。
从模版形式中容易看出,如果在图像中一个较暗的区域中出现了一个亮点,那么用拉普拉斯运算就会使这个亮点变得更亮。因为图像中的边缘就是那些灰度发生跳变的区域,所以拉普拉斯锐化模板在边缘检测中很有用。
一般增强技术对于陡峭的边缘和缓慢变化的边缘很难确定其边缘线的位置。但此算子却可用二次微分正峰和负峰之间的过零点来确定,对孤立点或端点更为敏感,因此特别适用于以突出图像中的孤立点、孤立线或线端点为目的的场合。同梯度算子一样,拉普拉斯算子也会增强图像中的噪声,有时用拉普拉斯算子进行边缘检测时,可将图像先进行平滑处理。
图像锐化处理的作用是使灰度反差增强,从而使模糊图像变得更加清晰。图像模糊的实质就是图像受到平均运算或积分运算,因此可以对图像进行逆运算,如微分运算能够突出图像细节,使图像变得更为清晰。由于拉普拉斯是一种微分算子,它的应用可增强图像中灰度突变的区域,减弱灰度的缓慢变化区域。因此,锐化处理可选择拉普拉斯算子对原图像进行处理,产生描述灰度突变的图像,再将拉普拉斯图像与原始图像叠加而产生锐化图像。
这种简单的锐化方法既可以产生拉普拉斯锐化处理的效果,同时又能保留背景信息,将原始图像叠加到拉普拉斯变换的处理结果中去,可以使图像中的各灰度值得到保留,使灰度突变处的对比度得到增强,最终结果是在保留图像背景的前提下,突现出图像中小的细节信息。但其缺点是对图像中的某些边缘产生双重响应。
最后我们来看看拉普拉斯算子的效果:


【十一】OpenCV读取图像的格式?
通常其他图像读取函数读取图片的时候是按RGB格式读取,但在OpenCV在读取图片时,是按BGR读取的。
【十二】中值滤波与均值滤波的相关概念
均值滤波也称为线性滤波,其采用的主要方法为邻域平均法。线性滤波的基本原理是用均值代替原图像中的各个像素值,即对待处理的当前像素点 ( x , y ) (x,y) (x,y),选择一个模板,该模板由其近邻的若干像素组成,求模板中所有像素的均值,再把该均值赋予当前像素点 ( x , y ) (x,y) (x,y),作为处理后图像在该点上的灰度值 g ( x , y ) g(x,y) g(x,y),即 g ( x , y ) = 1 m Σ f ( x , y ) g(x,y)=\frac{1}{m} \Sigma f(x,y) g(x,y)=m1Σf(x,y), m m m为该模板中包含当前像素在内的像素总个数。这样的方法可以平滑图像,速度快,算法简单。但是无法去掉噪声,但能微弱的减弱它。
中值滤波是一种非线性平滑技术,它将每一像素点的灰度值设置为该点某邻域窗口内的所有像素点灰度值的中值。具体实现过程如下:
- 通过从图像中的某个采样窗口取出奇数个数据进行排序。
- 用排序后的中值作为当前像素点的灰度值。
- 在图像处理中,中值滤波常用来保护边缘信息,是经典的平滑噪声的方法,该方法法对消除椒盐噪音非常有效,在光学测量条纹图象的相位分析处理方法中有特殊作用,但在条纹中心分析方法中作用不大。
----【计算机基础】----
【一】Linux中的进程状态种类
- 运行(正在运行或在运行队列中等待)
- 中断(休眠中,受阻,在等待某个条件的形成或等待接受到信号)
- 不可中断(收到信号不唤醒和不可运行,进程必须等待直到有中断发生)
- 僵死(进程已终止,但进程描述符存在,直到父进程调用wait4()系统调用后释放)
- 停止(进程收到SIGSTOP, SIGSTP, SIGTIN, SIGTOU信号后停止运行运行)
【二】Linux中ps aux指令与grep指令配合管理进程
ps相关指令
ps命令(Process Status)是最基本同时也是非常强大的进程查看命令。
- ps a 显示现行终端机下的所有程序,包括其他用户的程序。
- ps -A 显示所有程序。
- ps c 列出程序时,显示每个程序真正的指令名称,而不包含路径,参数或常驻服务的标示。
- ps -e 此参数的效果和指定"A"参数相同。
- ps e 列出程序时,显示每个程序所使用的环境变量。
- ps f 用ASCII字符显示树状结构,表达程序间的相互关系。
- ps -H 显示树状结构,表示程序间的相互关系。
- ps -N 显示所有的程序,除了执行ps指令终端机下的程序之外。
- ps s 采用程序信号的格式显示程序状况。
- ps S 列出程序时,包括已中断的子程序资料。
- ps -t <终端机编号> 指定终端机编号,并列出属于该终端机的程序的状况。
- ps u 以用户为主的格式来显示程序状况。
- ps x 显示所有程序,不以终端机来区分。
ps aux | more 指令
这个指令可以显示进程详细的状态。
参数解释:
- USER:进程的所有者。
- PID:进程的ID。
- PPID:父进程。
- %CPU:进程占用的CPU百分比。
- %MEM:进程占用的内存百分比。
- NI:进程的NICE值,数值越大,表示占用的CPU时间越少。
- VSZ:该进程使用的虚拟内存量(KB)。
- RSS:该进程占用的固定内存量(KB)。
- TTY:该进程在哪个终端上运行,若与终端无关,则显示?。若为pts/0等,则表示由网络连接主机进程。
- WCHAN:查看当前进程是否在运行,若为-表示正在运行。
- START:该进程被触发启动时间。
- TIME:该进程实际使用CPU运行的时间。
- COMMAND:命令的名称和参数。
- STAT状态位常见的状态字符:
D 无法中断的休眠状态(通常 IO 的进程);
R 正在运行可中在队列中可过行的;
S 处于休眠状态;
T 停止或被追踪;
W 进入内存交换 (从内核2.6开始无效);
X 死掉的进程 (基本很少見);
Z 僵尸进程;
< 优先级高的进程
N 优先级较低的进程
L 有些页被锁进内存;
s 进程的领导者(在它之下有子进程);
l 多进程的(使用 CLONE_THREAD, 类似 NPTL pthreads);+ 位于后台的进程组;
ps aux | grep xxx命令
如果直接用ps命令,会显示所有进程的状态,通常结合grep命令查看某进程的状态。
grep (global search regular expression(RE) and print out the line,全面搜索正则表达式并把行打印出来)是一种强大的文本搜索工具,它能使用正则表达式搜索文本,并把匹配的行打印出来。
例如我想要查看Python 的所有进程,可以在终端输入如下命令:
ps aux | grep python
便可以把Python相关的进程全部都打印到终端供我们查看。相关参数和之前的ps aux | more一致。
进程结束命令
我们可以使用kill命令来结束进程。
如下面的指令所示:
kill PID //杀掉进程
kill -9 PID //强制杀死进程
【三】Git,GitLab,SVN的相关知识
Git
Git是当前主流的一种开源分布式版本控制系统,可以有效、快速的进行项目版本管理。
Git没有中央服务器,不同于SVN这种需要中央服务器的集中式版本控制系统。
Git的功能:版本控制(版本管理,远程仓库,分支协作)
Git的工作流程:
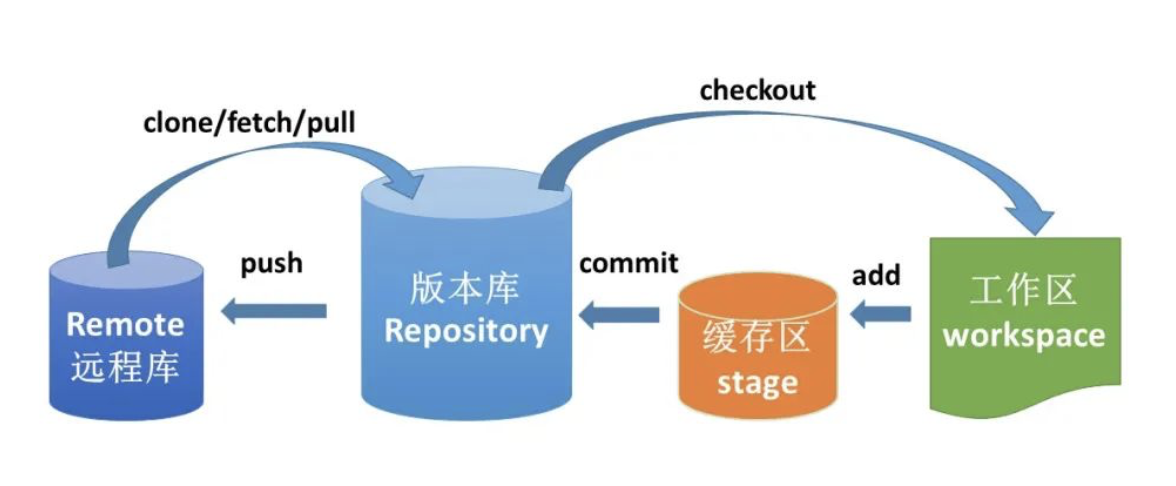
Git的常用命令:
git init 创建仓库
git clone 克隆github上的项目到本地
git add 添加文件到缓存区
git commit 将缓存区内容添加到仓库中
GitLab
GitLab是一个基于Git实现的在线代码仓库软件,可以基于GitLab搭建一个类似于GitHub的仓库,但是GitLab有完善的管理界面和权限控制,有较高的安全性,可用于企业和学校等场景。
SVN
SVN全名Subversion,是一个开源的版本控制系统。不同于Git,SVN是集中式版本控制系统。
SVN只有一个集中管理的服务器,保存所有文件的修订版本,而协同工作的人们都通过客户端连到这台服务器,取出最新的文件或者提交更新。
SVN的特点是安全,效率,资源共享。
SVN的常用操作:
Checkout 检出代码
Update 更新代码
Commit 提交代码
Add 提交新增文件
Revert to this version + commit 撤销已经提交的代码
【四】协程的相关概念
协程(Coroutine,又称微线程)运行在线程之上,更加轻量级,协程并没有增加线程总数,只是在线程的基础之上通过分时复用的方式运行多个协程,大大提高工程效率。
协程的特点:
- 协程类似于子程序,但执行过程中,协程内部可中断,然后转而执行其他的协程,在适当的时候再返回来接着执行。协程之间的切换不需要涉及任何系统调用或任何阻塞调用。
- 协程只在一个线程中执行,发生在用户态上的一个逻辑。并且是协程之间的切换并不是线程切换,而是由程序自身控制,协程相比线程节省线程创建和切换的开销。
- 协程中不需要多线程的锁机制,因为只有一个线程,也不存在同时写变量冲突,在协程中控制共享资源不加锁,只需要判断状态就好了,所以执行效率比多线程高很多。

协程适用于有大量I/O操作业务的场景,可以到达很好的效果,一是降低了系统内存,二是减少了系统切换开销,因此系统的性能也会提升。
在协程中尽量不要调用阻塞I/O的方法,比如打印,读取文件等,除非改为异步调用的方式,并且协程只有在I/O密集型的任务中才会发挥作用。
【五】Linux系统的相关概念
Linux系统是一种操作系统(Operating System简称OS),它是软件的一部分,是硬件基础上的第一层软件,即硬件和应用软件沟通的桥梁。
Linux系统系统会控制其他程序运行,管理系统资源,提供最基本的计算功能,如管理及配置内存、决定系统资源供需的优先次序等,同时还提供一些基本的服务程序。Linux系统内核指的是提供硬件抽象层、硬盘及文件系统控制及多任务功能的系统核心程序。Linux发行套件系统是由 Linux系统内核与各种常用应用软件的集合产品。
在Linux系统中一切都是文件。在linux系统中,目录、字符设备、块设备、套接字、打印机等都被抽象成了文件,Linux系统中的一切文件都是从“根(/)”目录开始的,并按照树形结构来存放文件,且定义了常见目录的用途,文件和目录名称严格区分大小写。
Linux系统的文件目录结构
- /usr:这是一个非常重要的目录,包含绝大多数的(多)用户工具和应用程序,用户的很多应用程序和文件都放在这个目录下,类似于windows下的program files目录。
- /lib:存放着系统开机时会用到的函数库,以及在/bin和/sbin下命令会调用的函数库,几乎所有的应用程序都需要用到这些共享库。
- /var:存放不断扩充的内容,如经常被修改的目录、文件(包括各种日志文件)等。
- /boot:存放启动Linux时所需的一些核心文件(linux内核文件),包括一些引导程序文件、链接文件、镜像文件等。
- /home:用户的主目录,在Linux中,每个用户都有一个自己的目录,该目录名一般以用户账号命名,包含保存的文件、个人设置等。
- /sbin:s就是Super User的意思,这里存放的是系统管理员使用的系统管理命令。
- /bin:这个存放的是当前用户的系统管理命令(cat、cp、ps等)。
- /etc:存放所有的系统管理所需的配置文件和子目录(例如人员的帐号密码文件,各种服务的起始文件等)。
- /tmp:存放一些临时文件,在系统重启时临时文件将被删除。
- /snap:Ubuntu 16.04及之后版本引入了snap包管理器,与之相关的目录、文件(包括安装文件)位于/snap中。
- /lost+found:该目录一般情况下是空的,当系统非法关机后会在该目录生成一些遗失的片段。
- /media:linux系统会自动识别一些设备,例如U盘、光驱等等,当识别后,linux会把识别的设备挂载到该目录下。
- /srv:该目录存放一些服务启动之后需要提取的数据。
- /root:该目录为系统管理员用户主目录。
- /opt:该目录存放安装的第三方软件,如Oracle数据库就可以安装到该目录下。
- /mnt:挂载其他的文件系统(含硬盘分区)的目录。
- /lib64:类似lib目录,存放64位库文件。
- /srv:可以视作service的缩写,是一些网络服务启动后,这些服务需要取用的数据目录,常见的服务例如www,ftp等。
- /proc:这个目录本身是一个虚拟文件系统,它放置的数据都是在内存当中,不占用硬盘的容量。
- /sys:这个目录其实跟/proc非常的相似,也是一个虚拟的文件系统主要也是记录与内核相关的信息,不占用硬盘容量。
- /dev:在linux中任何的设备和接口设备都是以文件的形式存在于这个目录当中。你只要到通过访问这个目录下的某个文件就相当于访问某个设备。
Linux系统种类
- 红帽企业版Linux:RedHat是全世界内使用最广泛的Linux系统。它具有极强的性能与稳定性,是众多生成环境中使用的(收费的)系统。
- Fedora:由红帽公司发布的桌面版系统套件,用户可以免费体验到最新的技术或工具,这些技术或工具在成熟后会被加入到RedHat系统中,因此Fedora也成为RedHat系统的试验版本。
- CentOS:通过把RedHat系统重新编译并发布给用户免费使用的Linux系统,具有广泛的使用人群。
- Deepin:在中国发行,对优秀的开源成品进行集成和配置。
- Debian:稳定性、安全性强,提供了免费的基础支持,在国外拥有很高的认可度和使用率。
- Ubuntu:是一款派生自Debian的操作系统,对新款硬件具有极强的兼容能力。Ubuntu与Fedora都是极其出色的Linux桌面系统,而且Ubuntu也可用于服务器领域。
【六】Linux系统和Windows系统的区别?
- Linux系统更稳定且有效率。
- Linux系统是免费(或少许费用),而Windows系统是商业化主导。
- Linux系统漏洞少且快速修补。
- Linux系统支持多用户同时使用计算机。
- Linux系统有更加安全的用户与文件权限策略。
- Linux系统可以访问源代码并根据用户的需要修改代码,而Windows系统不能访问源代码。
- Linux系统更能支持多种深度学习配套软件,但是windows系统能支持大量的视频游戏软件。
【七】POC验证测试的概念
POC(Proof of Concept),即概念验证。通常是企业进行产品选型时或开展外部实施项目前,进行的一种产品或供应商能力验证工作。主要验证内容:
- 产品的功能。产品功能由企业提供,企业可以根据自己的需求提供功能清单,也可以通过与多家供应商交流后,列出自己所需要的功能。
- 产品的性能。性能指标也是由企业提供,并建议提供具体性能指标所应用的环境及硬件设备等测试环境要求。
- 产品的API适用性。
- 产品相关技术文档的规范性、完整性。
- 涉及到自定义功能研发的,还需要验证API开放性,供应商实施能力。
- 企业资质规模及企业实施案例等。
验证内容归根结底,就是证明企业选择的产品或供应商能够满足企业提出的需求,并且提供的信息准确可靠。
POC测试工作的前提:
- 前期调研充分,并已经对产品或供应商有了比较深入的沟通了解。
- 企业对自己的产品需求比较清晰。
POC测试工作参与者:
使用用户代表、业务负责人、项目负责人、技术架构师、测试工程师、商务经理等。
POC测试工作准备文档:
- POC测试工作说明文档。内容包括测试内容、测试要求(如私有化部署)、测试标准、时间安排等。
- 功能测试用例。主要确认功能可靠性,准确性。内容包括功能名称、功能描述等。
- 场景测试用例。主要测试企业团队实施响应速度、实施能力、集成能力。这部分通常按照企业需求而定,不建议太复杂,毕竟需要供应商实施,拖的太久企业耐性受到影响,时间也会被拉长。
- 技术测评方案。主要验证产品的性能、功能覆盖情况、集成效率、技术文档的质量。
- 商务测评方案。主要包括企业实力、企业技术人才能力、版权验证、市场背景、产品报价等。
POC测试工作的主要流程:
第一阶段:工作启动
由商务或者对外代表对供应商发布正式邀请并附POC测试工作说明。
建立POC协同群。以满足快速沟通,应答。
涉及到私有化部署的,需要收集供应商部署环境要求,并与供应商一起进行部署工作,同时企业参与人员对部署工作情况做好记录。
第二阶段:产品宣讲及现场集中测试
供应商根据企业提供的POC测试工作说明及相应测试模块的用例或方案进行产品现场测试论证。
企业参与人员参与功能测试,并填写记录和意见。此阶段供应商往往需进行现场操作指导。
第三阶段:技术测评
供应商根据企业提供的技术要求给出相关支持技术文档,企业进行现场对比,根据实际情况进行统计记录。并保留供应商提供的资料和对比记录。
涉及到场景demo设计的,建议企业对实施人员能力、实施时长、实施准确性进行对比。
第四阶段:间歇性测试工作
该阶段是在第一阶段启动时,就可以开始了。测试功能外,还包括关键用户使用的体验心得、易用性评价。该部分允许企业用户主观评价,建议可以扩大范围组织间歇性测试,并做好测试用户记录。间歇时间1天或者多天根据实际情况安排。
第五阶段:商务验证
供应商根据企业提供的商务测评方案,积极配合工作。涉及到客户核实的,还需要企业进行考证。该部分工作也是从第一阶段启动时,就可以开始了。
第六阶段:背书归档、分析总结
每个阶段的工作都需要记录好参与人、时间、工作时间,并将测试过程中企业的、供应商的文档分类归档。对每个阶段进行分析对比,总结评价。最后进行整体工作分析总结。
POC工作按照不同企业和程度,测试的方式和投入力度不一样。但是目的都是相同的——验证产品或供应商能力是否满足企业需求。
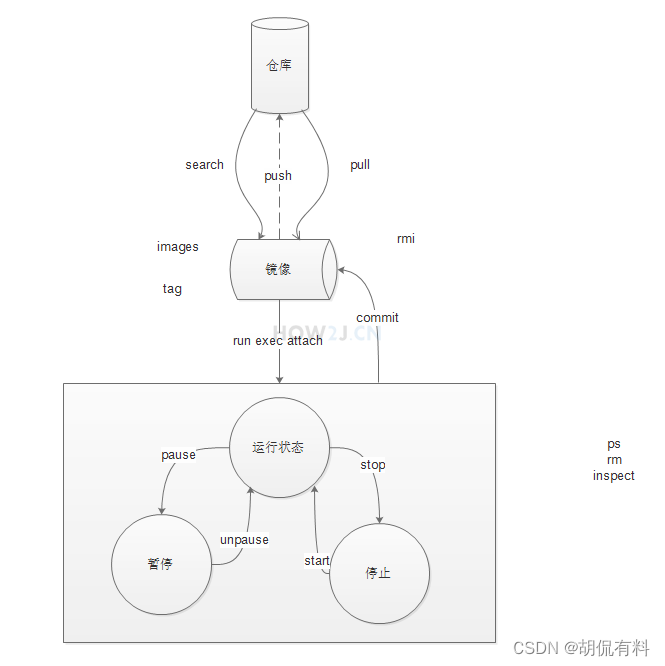
【八】Docker的相关概念及常用命令
Docker简介
Docker是一个开源的应用容器引擎,基于Go语言并遵从Apache2.0协议开源。
Docker可以打包代码以及相关的依赖到一个轻量级、可移植的容器中,然后发布到任何流行的Linux机器上,也可以实现虚拟化。
容器完全使用沙箱机制,相互之间不会有任何接口(类似iPhone的app),更重要的是容器性能开销极低。

Docker的应用场景:
- Web应用的自动化打包和发布。
- 自动化测试和持续集成、发布。
- 在服务器环境中部署/调整数据库或其它的后台应用。
Docker架构
Docker包括三个基本单元:
- 镜像(Image):Docker镜像(Image),就相当于是一个root文件系统。比如官方镜像ubuntu:16.04就包含了完整的一套Ubuntu16.04最简系统的root文件系统。
- 容器(Container):镜像(Image)和容器(Container)的关系,就像是面向对象程序设计中的类和实例一样,镜像是静态的定义,容器是镜像运行时的实体。容器可以被创建、启动、停止、删除、暂停等。
- 仓库(Repository):仓库可看成一个代码控制中心,用来保存镜像。
Docker容器使用
Docker客户端
Docker客户端非常简单,我们可以直接输入docker命令来查看到Docker客户端的所有命令选项。也可以通过命令docker command --help更深入的了解指定的Docker命令使用方法。
docker
容器使用
获取本地没有的镜像。如果我们本地没有我们想要的镜像,我们可以使用 docker pull 命令来载入镜像:
docker pull 镜像
启动容器。以下命令使用ubuntu镜像启动一个容器,参数为以命令行模式进入该容器:
docker run -it 镜像 /bin/bash
参数解释:
- -i:允许你对容器内的标准输入 (STDIN) 进行交互。
- -t:在新容器内指定一个伪终端或终端。
- /bin/bash:放在镜像名后的是命令,这里我们希望有个交互式Shell。
我们可以通过 <仓库名>:<标签> 的格式来指定具体是这个软件哪个版本的镜像。如果不给出标签,将以latest作为默认标签。
要退出终端,直接输入exit或者CTRL+D。
启动已经停止运行的容器。查看所有的容器的命令如下:
docker ps -a
我们也可以用docker ps命令查看正在运行的容器。
docker ps
我们可以使用 docker start 启动一个已停止的容器:
docker start 容器
想要后台运行容器,我们可以过 -d 指定容器的运行模式:
docker run -itd --name 指定创建的容器名 容器 /bin/bash
加了 -d 参数默认不会进入容器,想要进入容器需要使用下面的指令进入容器:
- docker attach
- docker exec:推荐大家使用 docker exec 命令,因为使用此命令退出容器终端,不会导致容器的停止。
docker attach 容器 //如果从这个容器退出,会导致容器的停止。
docker exec -it 容器 /bin/bash //如果从这个容器退出,不会导致容器的停止。
想要停止容器,其命令如下:
docker stop 容器ID
停止的容器重启命令:
docker restart 容器ID
删除容器:
docker rm -f 容器ID
Docker镜像使用
列出镜像列表。我们可以使用 docker images 来列出本地主机上的镜像。
docker images
各个参数解释:
- REPOSITORY:表示镜像的仓库源
- TAG:镜像的标签
- IMAGE ID:镜像ID
- CREATED:镜像创建时间
- SIZE:镜像大小
查找镜像:
docker search 镜像
各个参数解释:
- NAME: 镜像仓库源的名称
- DESCRIPTION: 镜像的描述
- OFFICIAL: 是否 docker 官方发布
- stars: 类似 Github 里面的 star,表示点赞、喜欢的意思。
- AUTOMATED: 自动构建。
删除镜像:
docker rmi 镜像
Docker镜像的修改和自定义
docker镜像的更新
在启动docker镜像后,写入一些文件、代码、更新软件等等操作后,退出docker镜像,之后在终端输入如下命令:
docker commit -m="..." -a= "..." 容器ID 指定要创建的目标镜像名称
参数解释:
- commit:固定格式
- -m:提交的描述信息
- -a:指定镜像作者
接着可以用docker images查看镜像是否更新成功。(注意:不要创建名称已存在的镜像,这样会使存在的镜像名称为none,从而无法使用)
镜像名称修改和添加新标签
更改镜像名称(REPOSITORY):
docker tag 容器ID 新名称
更改镜像tag,不修改名称:
docker tag IMAGEID(镜像id) REPOSITORY:TAG(仓库:标签)
Docker容器和本机之间的文件传输
主机和容器之间传输文件的话需要用到容器的ID全称。
从本地传输到容器中:
docker cp 本地文件路径 容器name:/root/(容器路径)
从容器传输到本地上:
docker cp 容器name:/root/(容器路径) 本地文件路径
Docker挂载宿主机文件目录
docker可以支持把一个宿主机上的目录挂载到镜像的目录中。
在启动docker镜像时,输入如下命令:
docker run -it -v /宿主机绝对路径:/镜像内挂载绝对路径 容器REPOSITORY /bin/bash
通过-v参数,冒号前为宿主机目录,冒号后为镜像内挂载的路径,必须为绝对路径。
如果宿主机目录不存在,则会自动生成,镜像里也是同理。
默认挂载的路径权限为读写。如果指定为只读可以用:ro
docker run -it -v /宿主机绝对路径:/镜像内挂载绝对路径:ro 容器REPOSITORY /bin/bash
【九】深度学习中常用的文件格式汇总
- csv:可用于方便的存储数据与标签。
- txt:最常见的文件格式,可用于存储数据路径与数据label。
- Json:是一种轻量级的数据交换格式,常用于保存数据label。
- Yaml:是一种数据序列化语言,通常用于编写配置文件,比如将网络模型配置参数与训练参数解耦至Yaml文件中,方便训练与优化。
- Cfg:Darknet中经典的保存网络模型结构的文件格式。
- Protobuf:是一个高效的结构化数据存储格式,可以存储神经网络的权重信息,在caffe中经常出现它的身影。
【十】TCP和UDP的区别?
- TCP面向连接,UDP是无连接的;
- TCP提供可靠的服务,也就是说,通过TCP连接传送的数据,无差错,不丢失,不重复,且按序到达;UDP尽最大努力交付,即不保证可靠交付;
- TCP的逻辑通信信道是全双工的可靠信道;UDP则是不可靠信道;
- 每一条TCP连接只能是点到点的;UDP支持一对一,一对多,多对一和多对多的交互通信;
- TCP面向字节流(可能出现黏包问题),本质上是TCP把数据看成一连串无结构的字节流;UDP是面向报文的(不会出现黏包问题);
- UDP没有拥塞控制,因此网络出现拥塞不会使源主机的发送速率降低(对实时应用很有用,如IP电话,实时视频会议等);
- TCP首部开销20字节;UDP的首部开销小,只需8个字节。
----【开放性问题】----
这些问题基于Rocky的思考提出,希望除了能给大家带来面试的思考,也能给大家带来面试以外的思考。这些问题没有标准答案,我相信每个人心中都有自己灵光一现的创造,你的呢?
【一】不同性质的公司如何使用好AI技术?
这是一个非常有价值的问题,随着AI技术进入全面的落地阶段,如何将AI技术与公司定位相适配,利用好AI技术并产生更多现金流闭环,成为未来各个公司重点考虑的问题。
【二】新时期的AI Lab该如何搭建?
深度学习发展至今,工业界,学术界,投资界都对其优势和局限有所判断了,基于此,各个公司的AI Lab也进入了全新的阶段,如何调整架构,如何改变定位,如何转变认知,是一件需要思考的事情。
【三】业务侧,竞赛侧,研究侧成果如何互相转化?
这是一个非常有价值的问题,随着宏观环境的变化,各个公司更加注重现金流,纯研究院等部门会被持续优化,这时如何高效的转化竞赛侧与研究侧的实用性成果,以及如何将业务侧经验向竞赛侧与研究侧延伸,成为各个公司重点考虑的问题。
【四】深度学习的优势和局限?
深度学习发展至今,工业界,学术界,投资界都对其优势和局限有所判断了。作为面试者,也需要对深度学习的趋势有所把握,不仅仅能在面试中进行交流,也能作为职业发展规划的一个先验知识。
【五】如何保持数据持续稳定的支持业务?
在“CV兵器”基本上都是开源的情况下,数据成为了支持业务迭代最重要的一部分,如何建立数据护城河,形成业务与数据双向正反馈,是AI行业从业者必须要面对的课题。
【六】如何分辨demo业务,一次性业务以及外包业务?
这个问题不仅可以考察面试者,面试者也可以用来反向判断面试官及其背后公司的运行逻辑。陷入demo业务,一次性业务以及外包业务的循环中是无法成长的,也不利于建立业务/产品的护城河。知道了这一点,那么如何去选择部门,如何去选择公司,如何去看需求,就变成了非常值得研究的事情。
【七】你觉得有哪些方法能增强公司的AI影响力?
AI除了落地,还有持续的愿景。这个问题启发我们,除了日常的技术深耕,也需要思考未来AI的发展趋势。如何扩大公司的AI影响力,是AI从业人员有必要去思考的一个维度。
【八】你觉得面对一个业务场景,如何针对性设计算法解决方案?
这是一个非常有价值的问题,随着的AI更加务实的落地,业务场景和算法解决方案的适配是非常关键的。如何获得针对性设计的能力,需要对现有现金流业务的深耕,以及提升产品侧视野的广度。
【九】对AI安全相关技术的发展前景的看法?
这是一个非常值得去思考的问题,在AI算法大范围落地之后,随之而来的就是安全风险,我相信AI安全将会是一个很大的课题。
【十】对GAN算法技术的发展前景的看法?
GAN的思想无疑让人眼前一亮,在目标检测,图像分割,图像分类等领域都有其辅助的身影,并在数据增强领域站在了舞台中央。
【十一】对一个零基础的CV算法学习者,有什么入门建议?
这是一个非常好的问题,既可以反映出面试者自身的CV学习入场逻辑,也能反映出面试者对于自己的学习过程是否有总结与提炼。
【十二】对CV算法技术的发展前景的看法?
我觉得这个问题可以从我经常提到的业务侧,竞赛侧,研究侧三个维度去思考和表达。在不同维度下,CV算法技术的发展前景会更加真实的体现,我们也能更从容地去表述我们的观点。
精致的结尾
最后,感谢大家读完这篇文章,希望能给大家带来帮助~后续Rocky会持续撰写“三年面试五年模拟”之独孤九剑的系列文章,大家敬请期待!






![[红明谷CTF 2021]write_shell](https://img-blog.csdnimg.cn/5ec9e56c361c4877a5f962bf9f51fc06.png)