递归
在编程中,我们把函数直接或者间接调用自身的过程叫做递归。
递归处理问题的过程是:通常把一个大型的复杂问题,转变成一个与原问题类似的,规模更小的问题来进行求解。
递归的三大要素
- 函数的参数。在用递归解决问题时,要合理地去设计函数的参数,达到当前问题与子问题之间的变化,可以通过参数进行准确地描述。
- 递推关系。要能够找到当前问题与子问题之间的联系,能够用子问题去描述当前问题的解。
- 递归出口(边界条件)。要找到问题的边界,避免出现无限递归的情况。每次我们在设计递归函数时,第一步就是先判断当前是否已经到达递归出口,若未到达则再继续递归。
偶数的递归定义
现在我们采用递归的方式来定义偶数:
- 0是一个偶数。
- 一个偶数与2的和是一个偶数。
这里我们在定义偶数时,就使用了偶数的这个概念。
证明10是偶数
现在我们需要使用刚才的定义来证明10是否为偶数。
因为10=8+2,根据第二条定义可以知道,一个偶数与2的和是一个偶数,现在我们只需要证明8是否是偶数即可得到结论。
我们现在用f(10)表示证明10是否为偶数的函数。
则整个的证明过程如下:
f(10) -> f(8) -> f(6) -> f(4) -> f(2) -> f(0),最终我们的问题变成证明0是否为偶数,而定义中已经给出0是偶数,所以我们可以得到2是偶数...依次类推。
f(0) -> f(2) -> f(4) -> f(6) -> f(8) -> f(10) 。
得出10是偶数。
参考代码
#include<bits/stdc++.h>
using namespace std;
bool f(int n){
if(n==0)//如果n==0,则n是偶数
return true;
return f(n-2); //否则证明n-2是否为偶数
}
int main(){
int n;
cin>>n;
cout<<f(n);
return 0;
}输入奇数会怎么样?
输入奇数就会无限递归下去,因为我们并没有为n是奇数的情况设计递归出口。如果n=7,就会去求n=5、3、1、-1、-3...一直递归下去。
我们可以在函数中添加,针对奇数情况的递归出口。(当n==1时,返回false)
训练:递归求和
请使用递归的方法,计算1+2+3+...+n的和。
【输入描述】1行:输入一个整数n。
【输出描述】1行:输出一个整数,表示求和的结果。
【样例输入】5
【样例输出】15
参考代码
#include<bits/stdc++.h>
using namespace std;
int sum(int n){
if(n==1)
return 1;
return sum(n-1)+n;
}
int main(){
int n;
cin>>n;
cout<<sum(n);
return 0;
}
训练:汉诺塔问题
汉诺塔(河内塔)问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
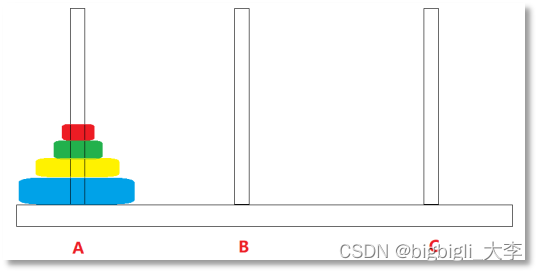
问题建模
我们可以使用4个参数去描述汉诺塔问题。
void Hanoi(int n,char a,char b,char c);
n表示移动的是第n号盘子;
a,b,c分别表示汉诺塔问题中的三个柱子。
我们称a,b,c分别为:起始柱,辅助柱,目标柱。
递归关系
- 根据游戏规则:想要移动n号盘,则需要先将n-1号盘从a柱移动到b柱。
此时我们的问题变成:Hanoi(n-1, a, c, b);
即:将n-1号盘从a柱出发,借助c柱,移动到b柱。
在这次移动的过程中a,c,b分别为:起始柱,辅助柱,目标柱。
- 将n-1号盘子移到b柱之后,我们就可以将n号盘子,直接从a移动到c,即:a->c。
到这一步,我们完成了第n号盘子的移动。
接下来我们还需要将n-1号盘子(在b柱),移动到c柱上。
即:Hanoi(n-1, b, a, c);
在这次移动的过程中b,a,c分别为:起始柱,辅助柱,目标柱。
边界条件
当问题变成只有一个盘子时,我们就无须借助辅助柱,
直接从a移动到c柱即可。
参考代码
void Hanoi(int n,char a,char b,char c){
if(n==1){
cout<<n<<":"<<a<<"->"<<c<<endl;
return ;
}
else{
Hanoi(n-1,a,c,b);
cout<<n<<":"<<a<<"->"<<c<<endl;
Hanoi(n-1,b,a,c);
}
}
int main(){
Hanoi(3,'a','b','c');
return 0;
}从C++入门到算法,再到数据结构,查看全部文章请点击![]() http://www.bigbigli.com/
http://www.bigbigli.com/