LeetCode[685]冗余连接II

news2024/9/22 17:36:14

难度：困难

题目：

在本问题中，有根树指满足以下条件的有向图。该树只有一个根节点，所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。

输入一个有向图，该图由一个有着 n 个节点（节点值不重复，从 1 到 n ）的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间，这条附加的边不属于树中已存在的边。

结果图是一个以边组成的二维数组 edges 。每个元素是一对 [ui, vi] ，用以表示有向图中连接顶点 ui 和顶点 vi 的边，其中 ui 是 vi 的一个父节点。

返回一条能删除的边，使得剩下的图是有 n 个节点的有根树。若有多个答案，返回最后出现在给定二维数组的答案。

示例 1：

输入：edges = [[1,2],[1,3],[2,3]]

输出：[2,3]

示例 2：

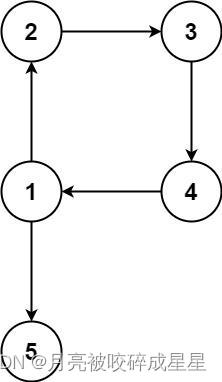
输入：edges = [[1,2],[2,3],[3,4],[4,1],[1,5]]

输出：[4,1]

提示：

n == edges.length

3 <= n <= 1000

edges[i].length == 2

1 <= ui, vi <= n

重点！！！解题思路

第一步：

明确解题手段
类似于此种连通性问题均能使用并查集来实现
但是这题我们需要将并查集稍微修改一下
已知此题要求每个节点的入度不能大于1
所以我们需要在并查集中添加一个记录每个几点入度的数组

第二步：

题中要求返回最后出现的答案，那么我就从后往前进行枚举
每次选中的不进行判断，
如果在这种情况下，其余节点全部连接成功并且没有连成一个环，并且每个节点的入度不>1
那么这次选中的数组则为多余值，
这个值即为答案

源码：

class UnionFind {
    //记录每个节点的根节点
    int[] parent;
    //记录每个子集的节点数
    int[] rank;
    //记录并查集中的联通分量数量
    int count;

    //每个节点的入度数量
    int[] vis;
    //是否有环
    boolean flag1;
    //是否入度大于1
    boolean flag2;

    public UnionFind(int n){
        count=n;
        parent=new int[n];
        for (int i=0;i<n;i++){
            parent[i]=i;
        }
        rank=new int[n];
        Arrays.fill(rank,1);
        flag1=false;
        flag2=false;
        vis=new int[n];
    }

    //路径压缩
    public int find(int ind){
        if (parent[ind]!=ind){
            parent[ind]=find(parent[ind]);
        }
        return parent[ind];
    }

    //按秩合并
    public void unite(int ind1,int ind2){
        int root1=find(ind1),root2=find(ind2);
        if (root1!=root2){
            if (rank[root1]<rank[root2]){
                int temp=root2;
                root2=root1;
                root1=temp;
            }
            parent[root2]=root1;
            rank[root1]+=rank[root2];
            count--;
        }else {//如果这两个节点的根节点相等了，说明这次判断成环了
            flag1=true;
        }
    }

    public int getCount(){
        return count;
    }
    public boolean connected(int ind1,int ind2){
        return find(ind1)==find(ind2);
    }
}
class Solution {
    public int[] findRedundantDirectedConnection(int[][] edges) {
        for (int i = edges.length-1; i >=0 ; i--) {
            int x=edges[i][0];
            int y=edges[i][1];
            UnionFind uf = new UnionFind(edges.length+1);
            for (int j=0;j<edges.length;j++){
                if (edges[j][0]==x&&edges[j][1]==y) continue;
                uf.unite(edges[j][0],edges[j][1]);
                if (uf.flag1) break;
                if (++uf.vis[edges[j][1]]>1){ //每次让下标为1的节点入度+1
                    uf.flag2=true;
                    break;
                }
            }
            if (!uf.flag1&& !uf.flag2){ //如果没成环，入度也是正常的，那么此次选中的待删除节点即为答案
                return new int[]{x,y};
            }
        }
        return null; //这里返回什么都可以，因为上面一定会返回一个值
    }
}

运行结果：