一，建模

1，重要性

实际上，我们并没有得到一个数学公式——通常问题是由某个领域的专家口头描述的。能够将问题转换成数学公式非常重要。建模并不是一件容易的事：有时，我们不仅想找到一个公式，还想找到一个好的公式。找到一个好的优化模型至少是解决问题的一半。

2，建模的一般步骤

• 分辨信息是否已知：已知为参数（parameter），未知为决策变量。
• 分辨决策变量
• 分辨任务目标：我们要实现什么？（目标函数）
• 分辨限制条件：我们需要满足什么？（约束）
• 对于目标函数和约束，我们应该能够使用决策变量写出一个公式/函数

二，例题描述

注：题目来自课件

1，最短路径问题

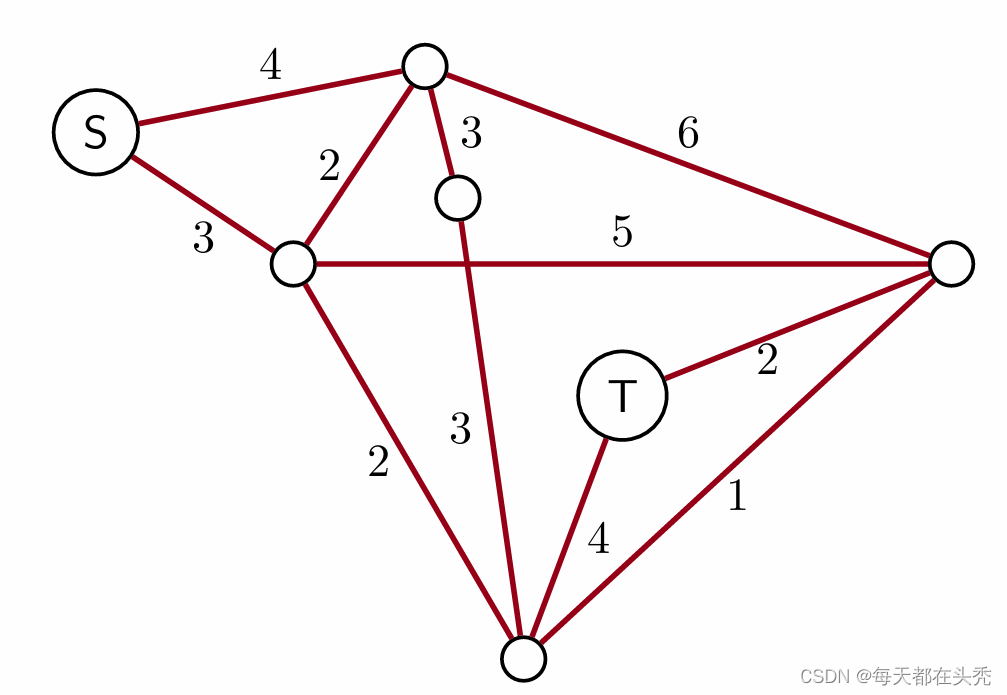
问题：S到T之间的最短路径是什么？

• 第一，二步：参数和决策变量

已知参数：图

决策变量：xij——是否使用这条边，如果使用xij=1，反之为0

• 第三步：目标函数

已知：我们要使S到T的路径最短

可知：要使总长d=最小，因此d的关系式就是目标函数

• 第三步限制条件

根据题意：1，连接起点和终点的边必须选一条

                  2，在本题中i到j和j到i的距离是相等的

                  3，xij——是否使用这条边，如果使用xij=1，反之为0

• 最后得到一个数学表达

示例：             minimize 

                          s.t.