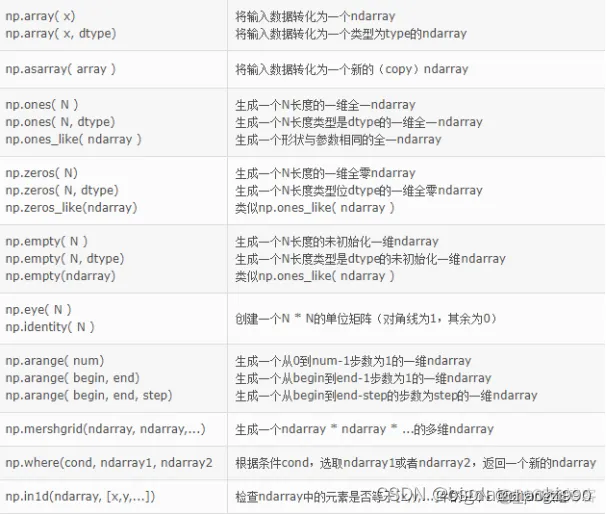
1、创建数组     

2、 与矩阵相关的函数

3、与排序相关的函数

4、 一元计算函数      

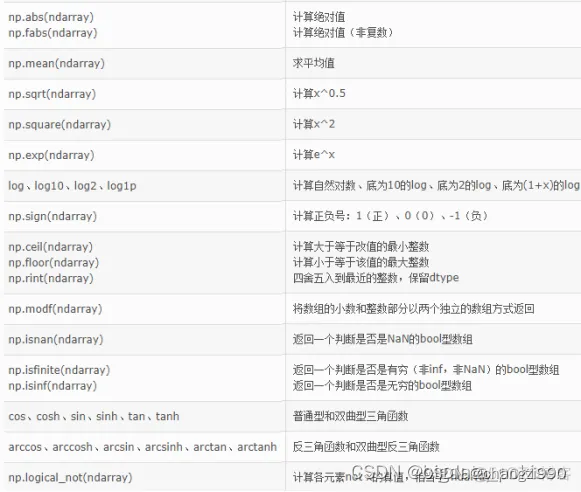
5、 多元计算函数     

6、 与文件读写相关的函数 

7、与数组形状、属性相关的函数

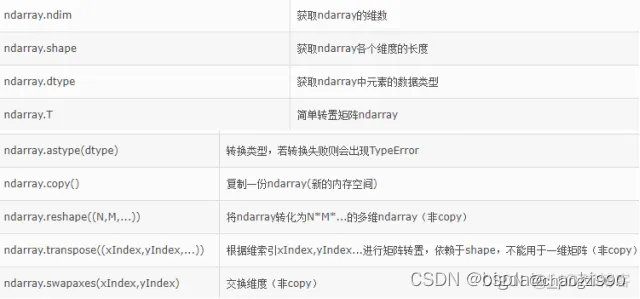
8、 常用计算函数   

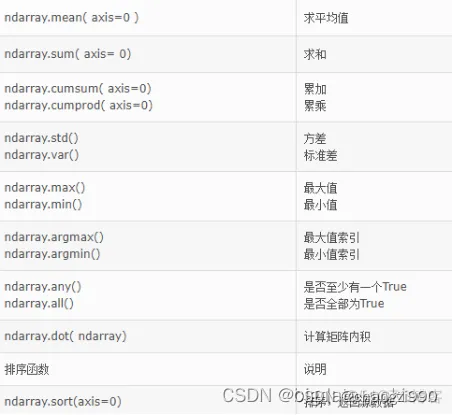
9、 数组选取：切片和索引    

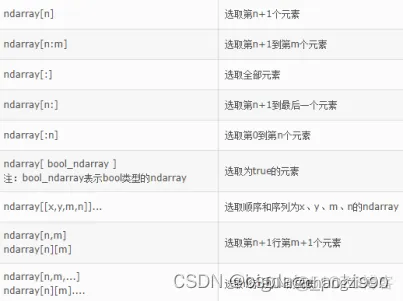
10、np.random相关函数    

Numpy常用的20个函数

一、创建数组
1、array
import numpy as np
np.array([1,2,3,4,5])
----------------
array([1, 2, 3, 4, 5, 6])
还可以使用此函数将pandas的df转为NumPy数组。
data={'小写':['a','b','c'],'大写':['A','B','C']}        
df=pd.DataFrame(data)
np.array(df)