55. 跳跃游戏

一、力扣示例

55. 跳跃游戏 - 力扣（LeetCode）https://leetcode.cn/problems/jump-game/55. 跳跃游戏55. 跳跃游戏 - 力扣（LeetCode）

二、解决办法

贪心

我们依次遍历数组中的每一个位置，并实时维护 最远可以到达的位置，赋值给rightmost，对于当前遍历到的位置 i，如果它 最远可以到达的位置 的范围大于等于数组中的最后一个位置，则返回true。

三、代码实现

public class Solution {
    public boolean canJump(int[] nums) {
        int n = nums.length;
        int rightmost = 0;
        for (int i = 0; i < n; ++i) {
            if (i <= rightmost) {
                rightmost = Math.max(rightmost, i + nums[i]);
                if (rightmost >= n - 1) {
                    return true;
                }
            }
        }
        return false;
    }
}

45. 跳跃游戏 II

一、力扣示例

45. 跳跃游戏 II - 力扣（LeetCode）https://leetcode.cn/problems/jump-game-ii/

二、解决办法

正向查找可到达的最大位置

在具体的实现中，我们维护当前能够到达的最大下标位置，记为边界。我们从左到右遍历数组，到达边界时，更新边界并将跳跃次数增加 1。

三、代码实现

class Solution {
    public int jump(int[] nums) {
        int n=nums.length;
        int rightmost=0;
        int count=0;
        int end=0;
        for(int i=0;i<n-1;i++){           
                rightmost=Math.max(i+nums[i],rightmost);
                if(i==end){
                    end=rightmost;
                    count++;
                }
           
        }
        return count;
    }
}

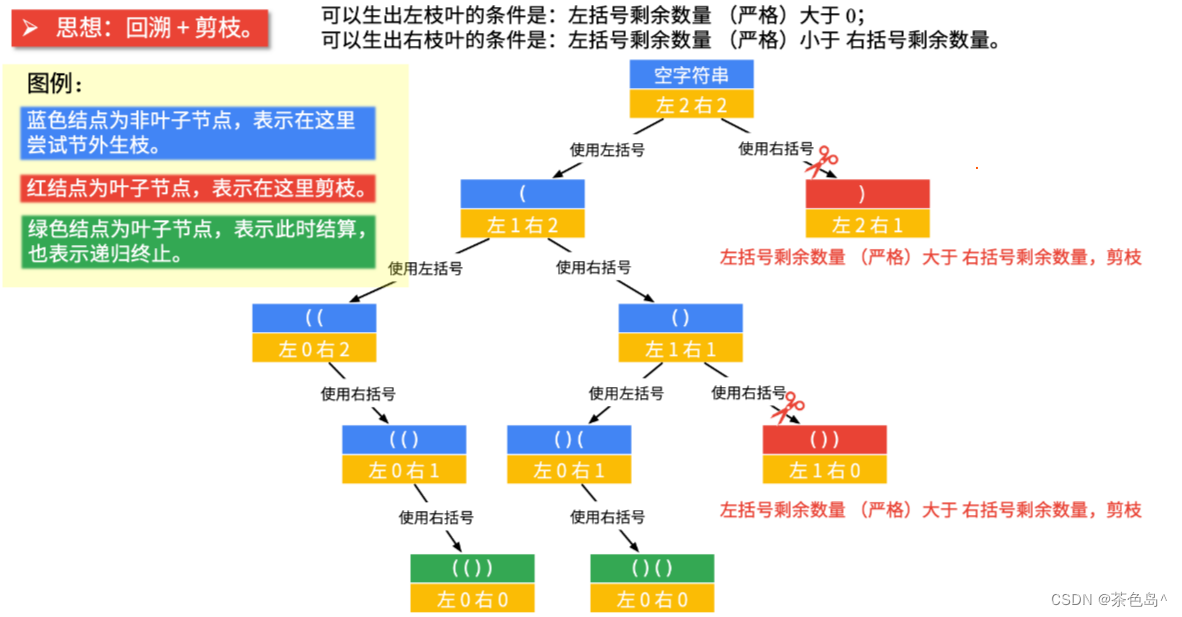
22. 括号生成

一、力扣示例

22. 括号生成 - 力扣（LeetCode）https://leetcode.cn/problems/generate-parentheses/

二、解决办法

深度优先遍历

三、代码实现

class Solution {
    public List<String> generateParenthesis(int n) {
           
        List<String> res = new ArrayList<>();        
        if (n == 0) {
            return res;
        }
        // 执行深度优先遍历，搜索可能的结果
        dfs("", n, n, res);
        return res;
    }

    public void dfs(String curStr, int left, int right, List<String> res) {
        
        if (left == 0 && right == 0) {
            res.add(curStr);
            return;
        }

        // 左括号可以使用的个数严格大于右括号可以使用的个数，才剪枝
        if (left > right) 
            return;       

        if (left > 0) 
            dfs(curStr + "(", left - 1, right, res);
        
        if (right > 0) 
            dfs(curStr + ")", left, right - 1, res);
        
    }


}

53. 最大子数组和

一、力扣示例

53. 最大子数组和 - 力扣（LeetCode）https://leetcode.cn/problems/maximum-subarray/

二、解决办法

动态规划

我们用 f(i) 代表以第 i 个数结尾的「连续子数组的最大和」
因此我们只需要求出每个位置的 f(i)，然后返回 f 数组中的最大值即可。
动态规划转移方程：f(i)=max{f(i−1)+nums[i],nums[i]}
考虑到 f(i) 只和 f(i−1) 相关，于是我们可以只用一个变量 pre 来维护对于当前 f(i) 的 f(i−1) 的值是多少，从而让空间复杂度降低到 O(1)，这有点类似「滚动数组」的思想。

三、代码实现

class Solution {
    public int maxSubArray(int[] nums) {
        int pre = 0, maxAns = nums[0];
        for (int x : nums) {
            pre = Math.max(pre + x, x);//以数x结尾的最大和
            maxAns = Math.max(maxAns, pre);
        }
        return maxAns;
    }
}