文章目录
- 问题提出
- 计算图中的神经网络
- 改进(激活函数)
- 反向传播
- 前馈计算
- 反向传播
- pytorch当中的前馈与反馈
- Tensor张量
- 课程代码
- 课后作业
课程来源: 链接
课程内容部分来源(觉得归纳的非常好的): 链接
以及(强烈推荐)BirandaのBlog!
问题提出
简单模型,直接可以利用损失函数对w的导数,来更新w
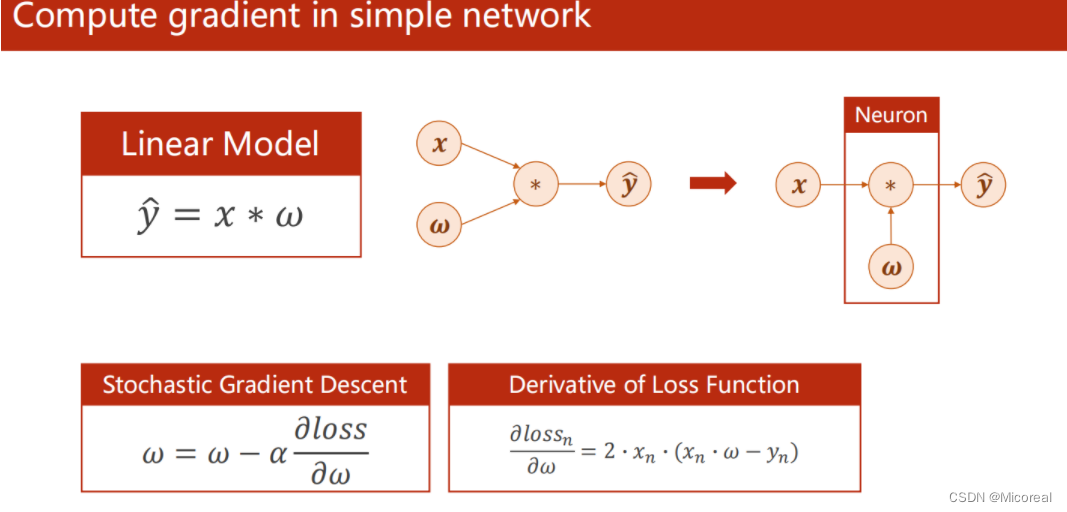
然而,对于复杂模型而言求解过程就复杂很多。在图示的神经网络中,每个结点为一个神经元,结点之间的连线为权重。记各符合表示如表所示:
| 符号 | 含义 |
|---|---|
| x i x_i xi | 输入层的第i个结点 |
| h i j h_{ij} hij | 第i层隐含层的第j个结点 |
| o i o_i oi | 输出层的第i个结点 |
| ω x 1 m n \omega_{x1}^{mn} ωx1mn | 输入层的第m个结点与隐含层的第n个结点之间的权重 |
| ω i j m n \omega_{ij}^{mn} ωijmn | 隐含层第i层的第m个结点与第j层的第n个结点之间的权重 |
| ω k o m n \omega_{ko}^{mn} ωkomn | 隐含层最后一层(第k层)的第m个结点与输出层第n个结点之间的权重 |

由图上可知,输入层与隐含层第一层之间就有
5
∗
6
=
30
5*6=30
5∗6=30个权重,隐含层的第一层与第二层之间又有
6
∗
7
=
42
6*7=42
6∗7=42个权重,以此类推,上图中共有
30
+
42
+
49
+
42
+
30
=
193
30+42+49+42+30=193
30+42+49+42+30=193个权重需要计算,传统得列表达式的方式是无法完成的。
计算图中的神经网络
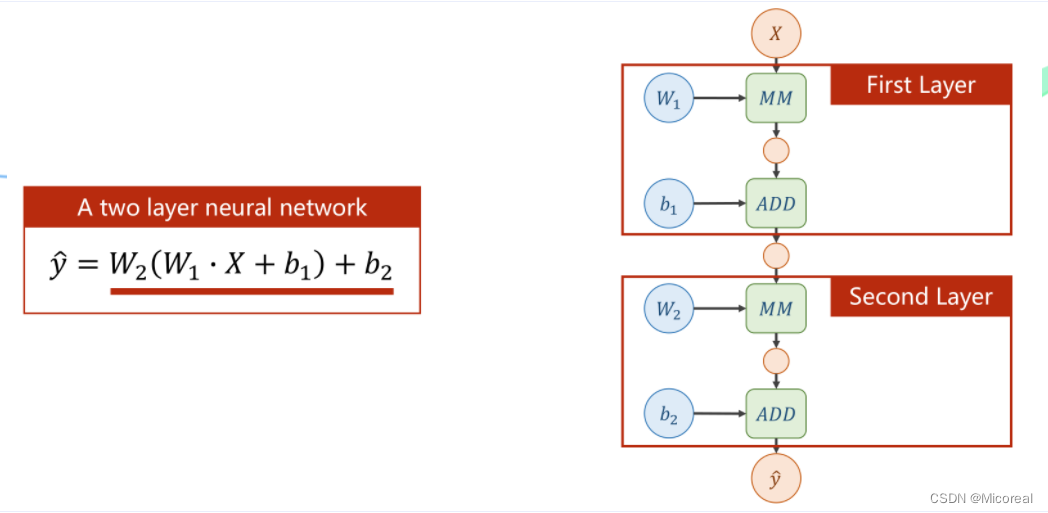
而上图左式中,可以化简得到如下公式
y
^
=
W
2
(
W
1
X
+
b
1
)
+
b
2
=
W
2
W
1
X
+
(
W
2
b
1
+
b
2
)
=
W
X
+
b
\widehat y = W_2(W_1X+b_1)+b_2=W_2W_1X+(W_2b_1+b_2)=WX+b
y
=W2(W1X+b1)+b2=W2W1X+(W2b1+b2)=WX+b
也就是说,在这个结构下单纯的增加层数,并不能增加神经网络的复杂程度,因为最后都可以化简为一个单一的神经网络(线性函数)
改进(激活函数)
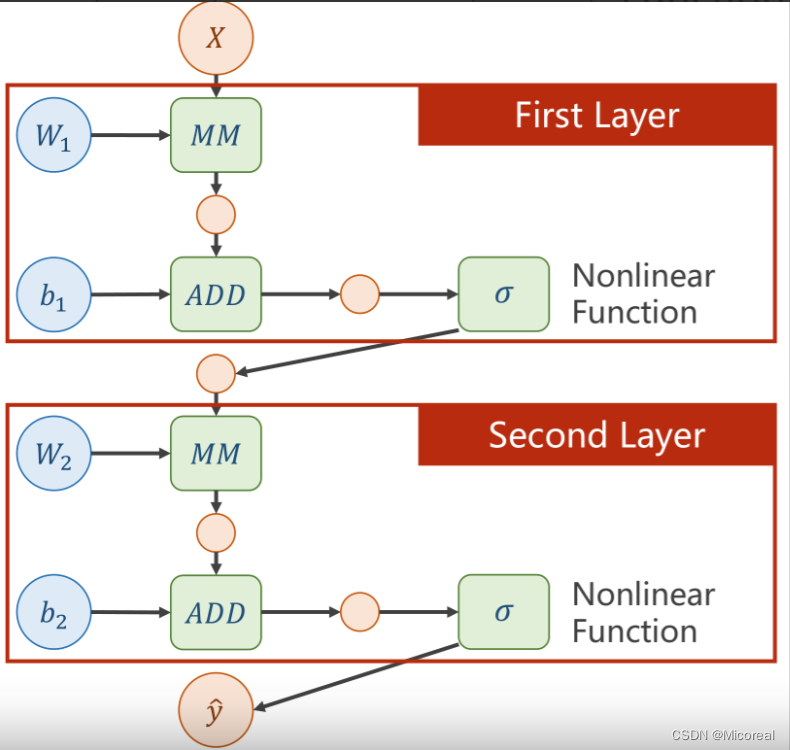
在每层网络结构中,增加一个非线性的变换函数(激活函数)
反向传播
前馈计算
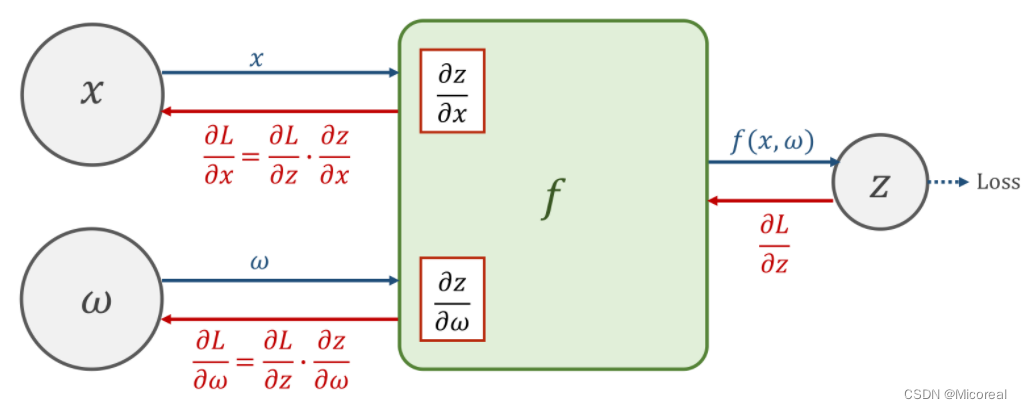
在某一神经元处,输入的 x x x与 ω \omega ω经过函数 f ( x , ω ) f(x,\omega) f(x,ω)的计算,可以获得输出值 z z z,并继续向前以得到损失值loss.
在向前计算的过程中,在 f ( x , ω ) f(x,\omega) f(x,ω)的计算模块中会计算导数 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z以及 ∂ z ∂ ω \frac{\partial z}{\partial \omega} ∂ω∂z,并将其保存下来(在pytorch中,这样的值保存在变量 x x x以及 ω \omega ω中)。
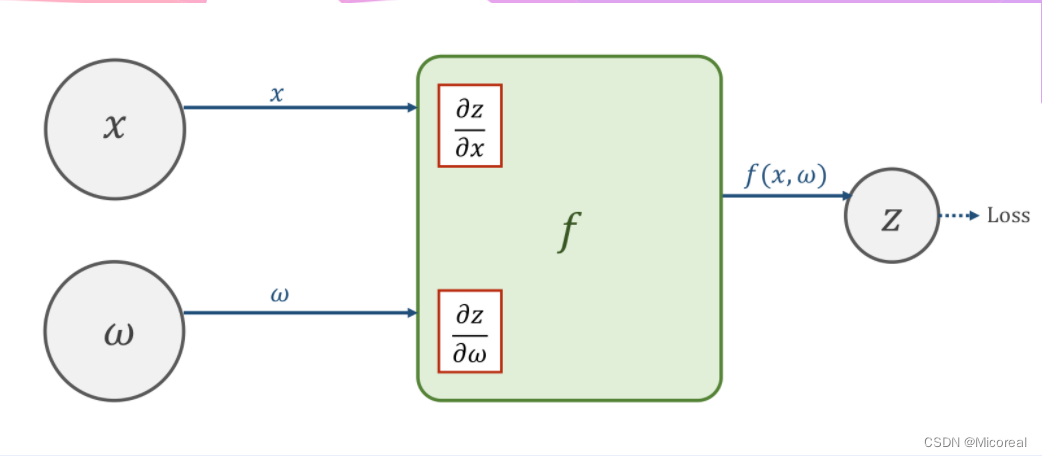
反向传播
由于求导的链式法则,求得loss以后,前面的神经元会将 ∂ l o s s ∂ z \frac{\partial loss}{\partial z} ∂z∂loss的值反向传播给原先的神经元,在计算单元 f ( x , ω ) f(x,\omega) f(x,ω)中,将得到的 ∂ l o s s ∂ x \frac{\partial loss}{\partial x} ∂x∂loss与之前存储的导数相乘,即可得到损失值对于权重以及输入层的导数,即 ∂ l o s s ∂ x \frac{\partial loss}{\partial x} ∂x∂loss,以及 ∂ l o s s ∂ ω \frac{\partial loss}{\partial \omega} ∂ω∂loss.基于该梯度才进行权重的调整。
pytorch当中的前馈与反馈
利用pytorch进行深度学习,最主要的是构建计算图
Tensor张量
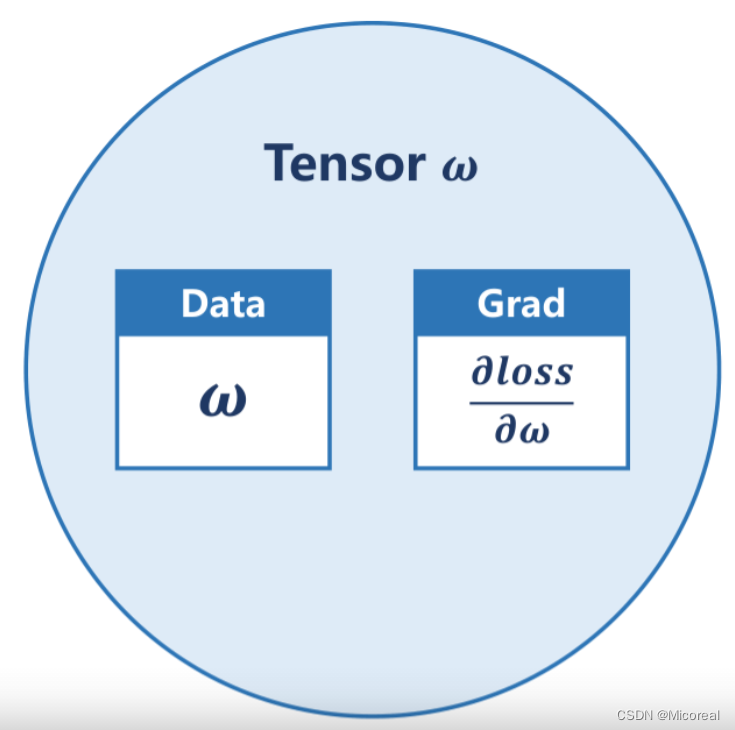
Tensor中重要的两个成员,data用于保存权重本身的值
ω
\omega
ω,grad用于保存损失函数对权重的导数
∂
l
o
s
s
∂
ω
\frac{\partial loss}{\partial \omega}
∂ω∂loss,grad本身也是个张量。对张量进行的计算操作,都是建立计算图的过程。
课程代码
import torch
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
#赋予tensor中的data
w = torch.Tensor([1.0])
#设定需要计算梯度grad
w.requires_grad = True
#模型y=x*w 建立计算图
def forward(x):
'''
w为Tensor类型
x强制转换为Tensor类型
通过这样的方式建立计算图
'''
return x * w
def loss(x, y):
y_pred = forward(x)
return (y_pred - y) ** 2
print ("predict (before training)", 4, forward(4).item())
for epoch in range(100):
for x,y in zip(x_data,y_data):
#创建新的计算图
l = loss(x,y)
#进行反馈计算,此时才开始求梯度,此后计算图进行释放
l.backward()
#grad.item()取grad中的值变成标量
print('\tgrad:',x, y, w.grad.item())
#单纯的数值计算要利用data,而不能用张量,否则会在内部创建新的计算图
w.data = w.data - 0.01 * w.grad.data
#把权重梯度里的数据清零
w.grad.data.zero_()
print("progress:",epoch, l.item())
print("predict (after training)", 4, forward(4).item())
课后作业
import torch
# 构造数据集
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]
# 初始化变量
w1 = torch.tensor([1.0],requires_grad=True)
w2 = torch.tensor([1.0],requires_grad=True)
b = torch.tensor([1.0],requires_grad=True)
# 构造连接式子
def forward(x):
return w1*x*x+w2*x+b
# 求取loss值
def loss(x,y):
y_val = forward(x)
return (y_val-y)**2
for epoch in range(10000):
for x,y in zip(x_data,y_data) :
# 计算loss
L = loss(x,y)
# 反向传播
L.backward()
# 通过loss修改权重
w1.data-=0.01*w1.grad.data
w2.data-=0.01*w2.grad.data
b.data-=0.01*b.grad.data
# 修改权重梯度当中的值
w1.grad.data.zero_()
w2.grad.data.zero_()
b.grad.data.zero_()
print(4,forward(4).item())

![[数据结构笔记]二叉树初阶](https://img-blog.csdnimg.cn/8ecad0af7f2d43eb8e45bfe34d76a17d.png)