上篇文章对HashMap的put方法进行了源码解析,并介绍了其中的两个亮点设计——位运算取代%和扰动计算。其中还有几个细节,比如每次扩容都是2^n是怎么做到的、JDK1.8增加的红黑树结构,由于篇幅原因没有介绍,本节就先来介绍其中的一个细节——红黑树。
一、JDK 1.8为什么增加树结构
上节也提到过,HashMap是通过链地址法解决哈希冲突的,也就是当发生冲突时,新的元素会挂到当前桶的链表中。
这样就会有一个问题,当hash冲突过多,链表就会挂的很长,我们知道,链表越长,它的查询性能就无限趋于O(N),这样显然是不能接收的。
虽然JDK 1.8和1.7的扰动计算,尽可能地使key分散开来,但是效果并不理想,所以当链表过长的时候,就只能对其数据结构进行修改来增加效率。
毫无疑问,最先想到的就是树结构,那么树结构有很多选择,为什么最终选择了红黑树呢?
二、为什么选红黑树
2.1 二查查找树
关于查询效率,我们首先想到的应该使二叉查找树,它的特点就是左节点<root节点<右节点,这样遍历的复杂度就从链表的O(N)变为了O(logN)。
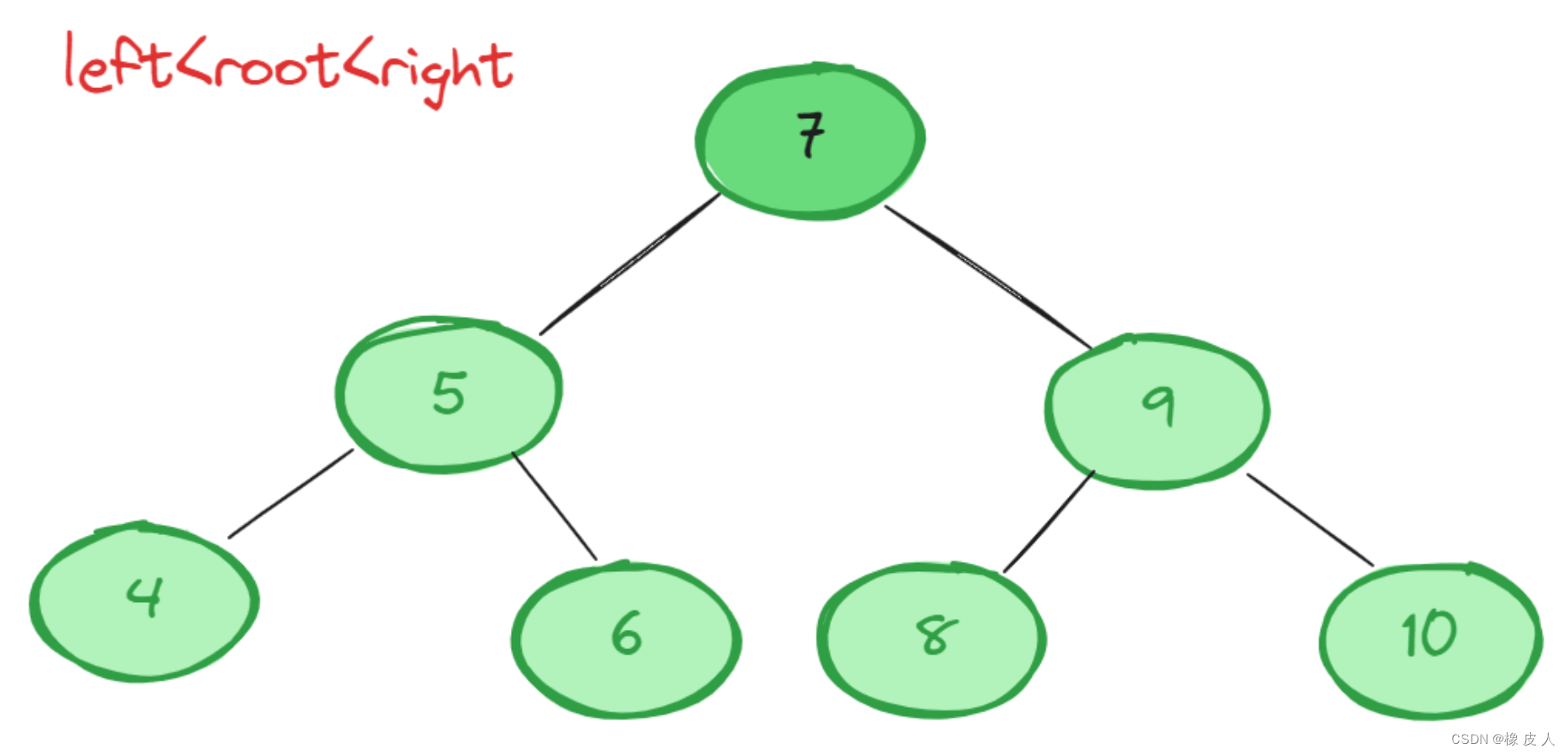
但是,但在极端情况下二查查找树会退化为链表,当子节点都比父节点都大或都小时:

2.2 平衡二叉树(AVL树)
二查查找树在最差的情况下竟然和顺序查找效率相当,这是无法接受的。我们再来看看平衡二叉树。
AVL是严格平衡的二叉树(平衡因子不超过1),每一次插入数据会检查每个节点的左子树和右子树的高度差,如果大于1,就需要进行左旋或右旋操作,因此查询效率最好,最坏的情况都是O(logN)。
不过这是有代价的:
插入操作:由于AVL必须严格保证平衡,那么每次插入数据,如果平衡因子大于1,就必须进行旋转操作,事实上每次插入操作最多只需要旋转1次,所以插入操作的代价仍是O(logN)。
删除操作:AVL删除可以参考二叉树的删除,但是删除之后必须检查从删除节点开始到根节点路径上的所有结点的平衡因子,这样代价就比较大了,每次删除最多需要O(logN)次旋转,因此删除操作的复杂度为O(2logN)。
综上可以发现,对于那些频繁删除和插入的场景,AVL树显然不合适,所以就引入了红黑树。
2.3 红黑树
平衡二叉树严格平衡的策略是以牺牲插入和删除操作为代价,换来的查询效率(O(logN)。是否能找一个这种的策略,既不会让插入和删除操作牺牲太大的代价,又能把查询的效率稳定在O(logN)呢?
当然有,那就是红黑树,先来看下它的特点:
每个节点不是黑色就是红色,根节点永远是黑色。
所有的叶子结点都是黑色的空节点,也就是叶子节点不存数据。
当一个节点是红色,那么它的子节点必定是黑色的。
一个节点的所有子孙节点到该节点的所有路径上,包含相同数目的黑色节点。
如下图:

我们来对比下AVL树:
查询操作:红黑树不像AVL一样是严格平衡的,但查找的效率基本可以维持在O(logN),最差的情况下(最长路径是最短路径的2n-1),比AVL逊色。
插入操作:插入节点时,需要旋转和变色操作。但只需要保证基本平衡就可以了,因此插入节点最多只需要2次旋转,虽然变色需要O(logN),但变色操作十分简单,代价很小。
删除操作:在删除上就比AVL好多了,删除一个节点最多只需要3次旋转操作。
综上,这就是HashMap选择红黑树的原因。
三、红黑树和链表的转换时机
OK,我们回到代码来,通过上一节我们知道,数组长度大于64&&链表长度大于8,会转为红黑树,我们背过八股文的都知道,当红黑树节点小于等于6时又会转为链表,那么这些临界值是怎样考量的呢?
3.1 红黑树转链表的时机
为什么组长度大于64 && 链表长度大于8,才转为红黑树呢?
ps:首先明确一点,红黑树占用的空间是链表的2倍。
我们知道当数组长度小于64时,不会转为红黑树,而是会选择扩容,这也不难想到,因为数组长度小于64时,说明目前的数据量比较小,没必要转为红黑树。
而链表长度大于8呢?我们先来看一段源码注释:
/* Because TreeNodes are about twice the size of regular nodes, we
* use them only when bins contain enough nodes to warrant use
* (see TREEIFY_THRESHOLD). And when they become too small (due to
* removal or resizing) they are converted back to plain bins. In
* usages with well-distributed user hashCodes, tree bins are
* rarely used. Ideally, under random hashCodes, the frequency of
* nodes in bins follows a Poisson distribution
* (http://en.wikipedia.org/wiki/Poisson_distribution) with a
* parameter of about 0.5 on average for the default resizing
* threshold of 0.75, although with a large variance because of
* resizing granularity. Ignoring variance, the expected
* occurrences of list size k are (exp(-0.5) * pow(0.5, k) /
* factorial(k)). The first values are:
*
* 0: 0.60653066
* 1: 0.30326533
* 2: 0.07581633
* 3: 0.01263606
* 4: 0.00157952
* 5: 0.00015795
* 6: 0.00001316
* 7: 0.00000094
* 8: 0.00000006
* more: less than 1 in ten million
*/大概意思就是:
理想情况下,使用随机的哈希码,节点分布在hash桶中的频率遵循泊松分布,按照泊松分布的公式计算,因为哈希冲突造成桶的链表长度为8时的概率只有0.00000006,这个概率足够低了,并且到8个节点时,红黑树的性能优势也会开始展现出来,因此8是一个比较合理的数字。
3.2 链表转红黑树的时机
对于同一个索引位置,当红黑树节点小于等于6时,就会触发红黑树转链表。(这个扩容的时候会讲)。
经过3.1小节的介绍,这也不难理解,主要原因还是对于性能和空间的考虑,那为什么不能在小于8的时候立刻转会来呢?
如果8的时候转红黑树,小于8就立刻转回来,那么这就可能导致频繁的转换,所以要选择一个小于8的临界值,但又不能是7,从前面的泊松分布可以看到,当红黑树节点小于6时,它所带来的优势其实已经没有那么大了,就不足以抵消由于红黑树维护节点所带来的额外开销,此时转换回来能节省空间和时间。
四、红黑树的双向链表
看过源码的同学会发现,HashMap红黑树的数据结构中,不仅有常见的parent、left、right节点,还有一个next和prev节点。这说明它不仅是一个红黑树,还是一个双向链表。

这样做的原因:
红黑树会记录树化之前的链表结构,这样当红黑树退化成链表的时候,就可以直接按照链表重新链接的方式进行。
不过可能有人会问,那不是需要一个next节点就行了,为啥还要prev呢?
如果删除的是原始链表的中间节点,只靠next是无法将原始的链表重新连接的,所以就需要有prev节点,找到上一个节点,重新连接。
End:希望对大家有所帮助,如果有纰漏或者更好的想法,请您一定不要吝啬你的赐教🙋。