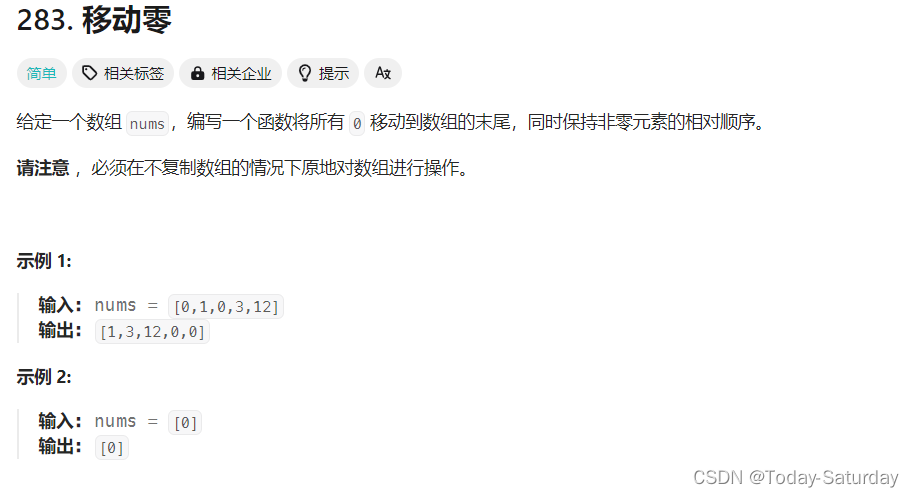
我们先看一下题目描述：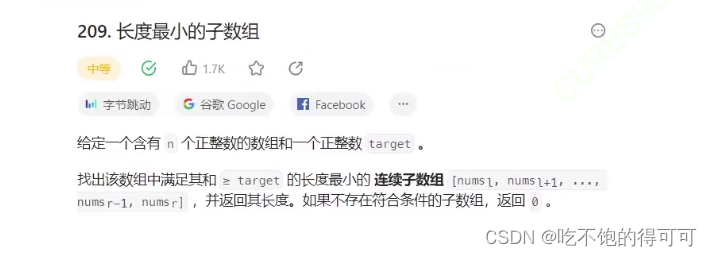

 

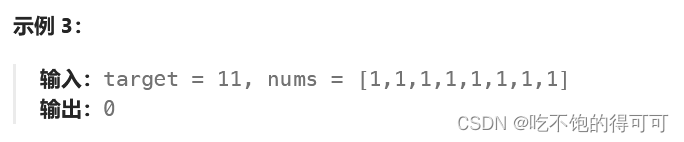
解法一：暴力枚举

时间复杂度：o(n^3)

class Solution {
public:
	int minSubArrayLen(int target, vector<int>& nums)
	{
		int i = 0, j = 0;
		vector<int> v;
		for (;i < nums.size();i++)
		{
			int sum = nums[i];
			for (j = i + 1;j < nums.size();j++)
			{
				sum = sum + nums[j];
				if (target == sum)
				{
					v.push_back(j - i + 1);//j-i+1就是满足条件的子数组的长度
					break;
				}
			}
		}
		sort(v.begin(), v.end());
		if (v.empty())
			return 0;
		else
			return v[0];
	}
};

解法2：利用数组元素的单调性，滑动窗口（同向双指针）算法。

时间复杂度： o(n)

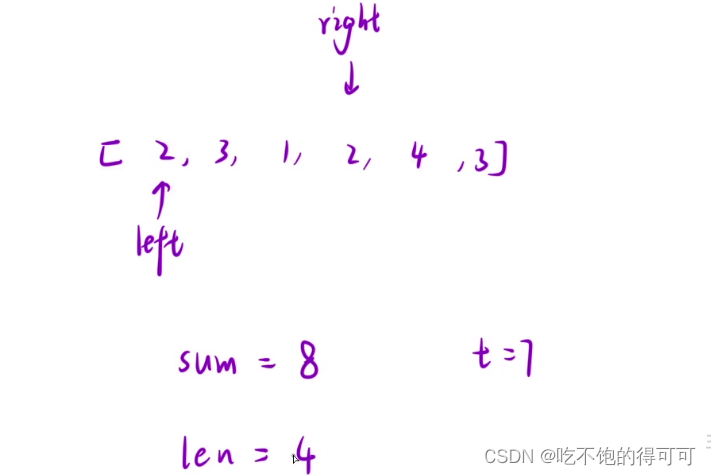
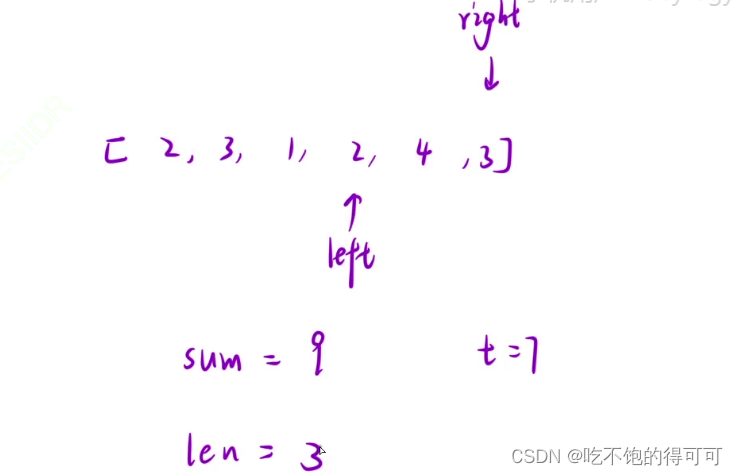
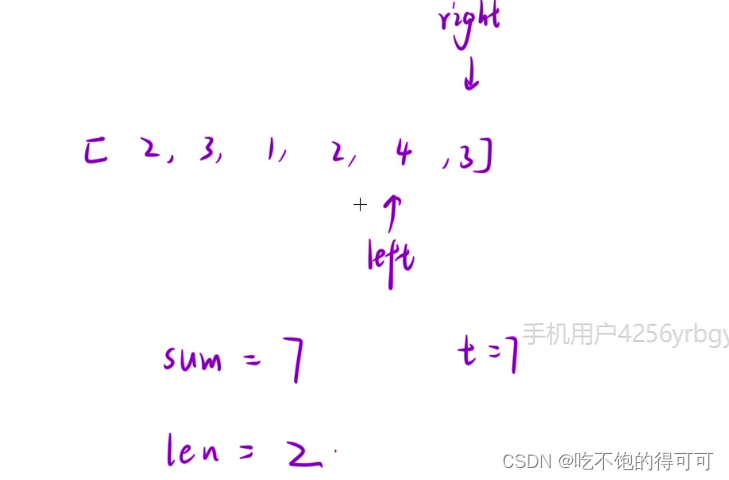
滑动窗口怎么用呢？

1、left=0,right=0

2、进窗口-->判断是否满足条件-->否-->进窗口

                                                      是-->更新结果-->出窗口-->更新结果

滑动窗口算法主要是利用数组元素之和的单调性，规避了很多没有必要的枚举行为。

下面是滑动窗口算法的演示：

 

 

 

下面我们来实现一下基于滑动窗口算法的解题代码：

class Solution {
public:
	int minSubArrayLen(int target, vector<int>& nums)
	{
		int sum = 0, len = INT_MAX;
		for (int left = 0, right = 0;right < nums.size();right++)
		{
			sum += nums[right];//进入窗口
			while (sum >= target)//判断
			{
				len = min(len, right - left + 1);//更新结果
				sum -= nums[left++];//出窗口
			}
		}
		return len == INT_MAX ? 0 : len;
	}
};