LeetCode刷题之HOT100之不同的二叉搜索树

news2024/11/24 15:52:05

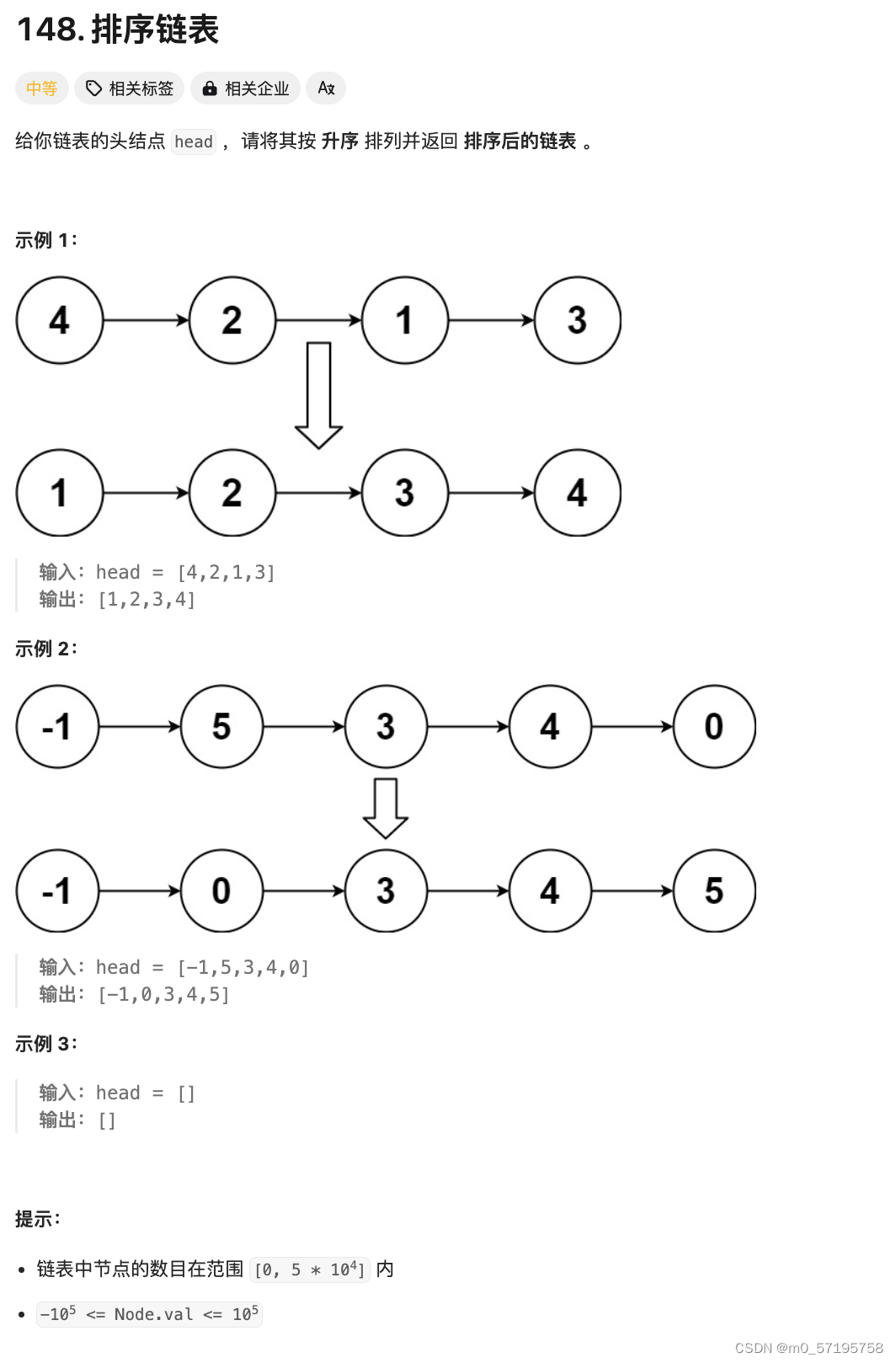
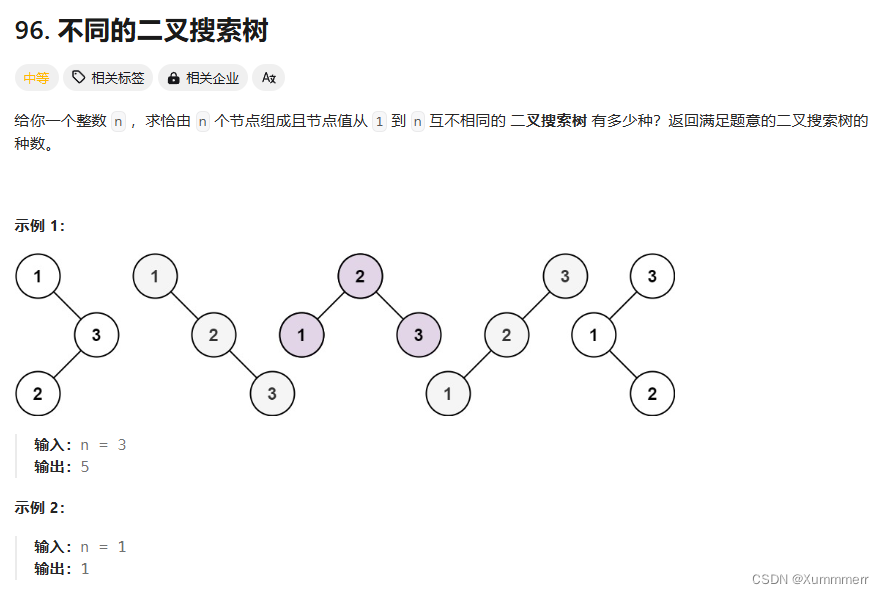
1、题目描述

在这里插入图片描述

2、逻辑分析

给定一个有序序列 1⋯n，为了构建出一棵二叉搜索树，我们可以遍历每个数字 i，将该数字作为树根，将 1⋯(i−1) 序列作为左子树，将 (i+1)⋯n 序列作为右子树。接着我们可以按照同样的方式递归构建左子树和右子树。

3、代码演示

 public int numTrees(int n) {
        // 创建一个长度为 n+1 的数组，用于存储从 0 到 n 的节点数量对应的二叉树数量 
        int dp[] = new int[n + 1];
        // 当节点数量为 0 时，只有一个空树（即没有节点的树）
        dp[0] = 1 ;
        // 当节点数量为 1 时，只有一个节点构成的树
        dp[1] = 1 ;
        // 从 2 开始遍历到 n，因为 0 和 1 的情况已经初始化了
        for(int i = 2; i <= n ; i++){
            // 对于每个 i（节点数量），我们需要遍历所有可能的根节点位置 j（从 1 到 i）
            for(int j = 1; j <= i; j++){
                // 对于每个根节点位置 j，左子树有 j-1 个节点，右子树有 i-j 个节点  
                // 因此，左子树可能的二叉树数量是 dp[j - 1]，右子树可能的二叉树数量是 dp[i - j]  
                // 所以，以第 j 个节点为根节点的二叉树数量是 dp[j - 1] * dp[i - j]  
                // 我们需要累加所有可能的根节点位置 j 的二叉树数量  
                dp[i] += dp[j -1] * dp[i - j];
            }
        }
        // 返回节点数量为 n 的不同二叉树数量
        return dp[n];     
    }

这段代码的核心思想是：对于 n 个节点的二叉树，我们遍历所有可能的根节点位置，并计算以该节点为根节点时，左右子树的所有可能组合。最后，累加所有根节点位置的结果，得到总的二叉树数量。
时间复杂度： $O(n^{2})$ 。空间复杂度：O(n)。
还有一种数学公式也可以解决此问题：这种计算结果在数学上被称为卡塔兰数，公式： $C_0=1,\quad C_{n+1}=\frac{2(2n+1)}{n+2}C_n$
下面是代码实现

public int numTrees(int n) {
        // 提示：我们在这里需要用 long 类型防止计算过程中的溢出
        long C = 1;
        for (int i = 0; i < n; ++i) {
            C = C * 2 * (2 * i + 1) / (i + 2);
        }
        return (int) C;
    }