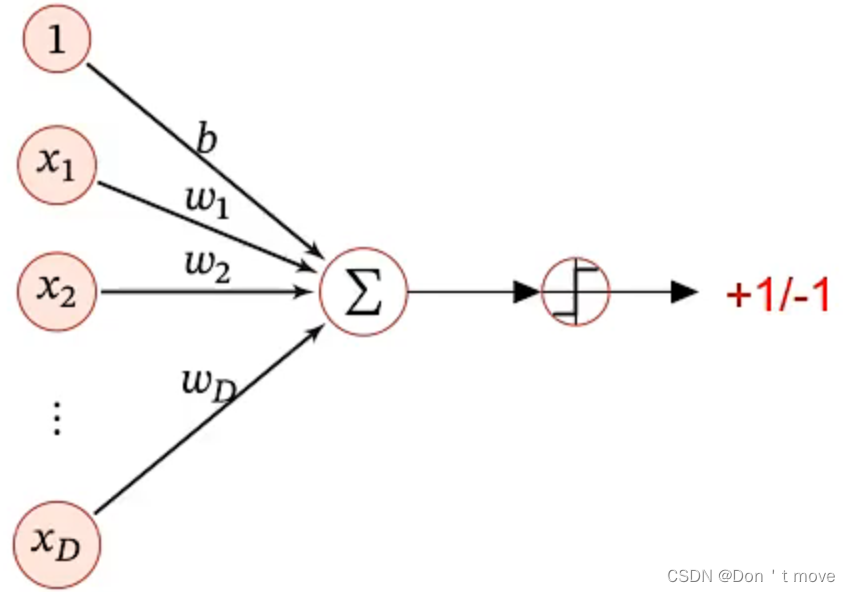
感知器是一种非常早期的线性分类模型，作为一种简单的神经网络模型被提出。感知器是一种模拟生物神经元行为的机器，有与生物神经元相对应的部件，如权重（突触）、偏置（阈值）及激活函数（细胞体），输出为+1或-1。

模型

感知器的模型结构与其他回归函数相同，都是对线性模型的复合。

$$\hat{y}=\mathrm{sgn}(w^{T}x)$$
但是与之前那些线性分类模型不同的是，感知器的输出在区间$(-1,1)$上

学习目标

在保证数据集线性可分的情况下（$w^{\ast }$存在），对于训练集$\{(x^{(n)},y^{(n)}){\}}_{n=1}^N$，找到最优权重$w^{\ast }$使得：
y ( n ) w ∗ T x ( n ) > 0 ,    ∀ n ∈ { 1 , ⋯   , N } y^{(n)}{w^*}^Tx^{(n)}>0,\ \ \forall n\in\{1,\cdots,N\} y(n)w∗Tx(n)>0,  ∀n∈{1,⋯,N}
举例来说，假设一个样本中$y=1$，如果上式<0则说明预测值$\hat{y}={w^{\ast }}^{T}x=-1$，也就是说预测值与真实值不同，意味着该样本的分类不是正确的分类；反之则意味着样本被分到了正确的分类中。

优化方法：一种错误驱动的在线学习算法

• 在线学习：数据是流式传输、一个一个的过来的，类似于从队列取出数据来进行学习，完成一次迭代后从头重新开始再一个一个进行学习。
• 错误驱动：在数据预测错误时才对参数进行更新，否则不更新

首先初始化一个权重向量$w\leftarrow 0$（通常是全零向量），每次分错一个样本（即$y{w}^{T}x<0$）则更新权重
$$w\leftarrow w+yx$$
至于为什么要这样更新，可以看一个例子：如果$y{w_t}^{T}x<0$，那么更新参数$w_{t+1}=w_t+yx$，更新后$y{w_{t+1}}^{T}x=y(w_t+yx{)}^{T}x=y{w_t}^{T}x+y{y}^T{x}^{T}x=y{w_t}^{T}x+y^2\parallel x{\parallel }^2$，其中后项$y^2\parallel x{\parallel }^2>0$，因此最终$y{w_{t+1}}^{T}x\ge y{w}_t^{T}x$，经过多次迭代后，最终可以让这个结果>0。
感知器这种学习策略实际上与梯度下降的迭代过程非常类似，用这种思想，可以反推感知器的损失函数。按照随机梯度下降的迭代思路，对于一个样本，将$yx$看作含梯度的项，同时参数优化方向与梯度方向相反，得：
$$\begin{array}{rl}\frac{\partial \mathcal{L}(w)}{\partial w}& =\{\begin{array}{rl}-yx& ify{w}^{T}x<0\\ 0& ify{w}^{T}x>0\end{array}\\ & \\ \mathcal{L}(w)& =\{\begin{array}{rl}-y{w}^{T}x& ify{w}^{T}x<0\\ C& ify{w}^{T}x>0\end{array}\end{array}$$
因此损失函数为
$$\mathcal{L}(w;x,y)=\max (0,-y{w}^{T}x)$$
也就是说，当样本分类正确（$y{w}^{T}x>0$）时损失为0，分类错误（$y{w}^{T}x<0$）时损失为$-y{w}^{T}x$

下面是对错误驱动算法的伪代码描述

其中，随机排序的目的是为了保证了样本的随机性，不受少数几个样本的影响，如果已知保持训练集顺序不变就会导致训练集后面几个样本的权重大。其次，达到最大迭代次数也可以是在验证集上收敛。
相比Logistic回归，感知器不需要比较预测值与真实值之间的差异（$y^{(n)}-{\hat{y}}^{(n)}$）。也就是说，感知器不比较犯错误的程度有多大，而Logistic回归需要比较犯错误程度，但凡有一点偏差就要纠正，二者在不同的场景下各有优劣。
下面是一个感知器参数学习的更新过程示例，其中空心点表示负例，实心表示正例：

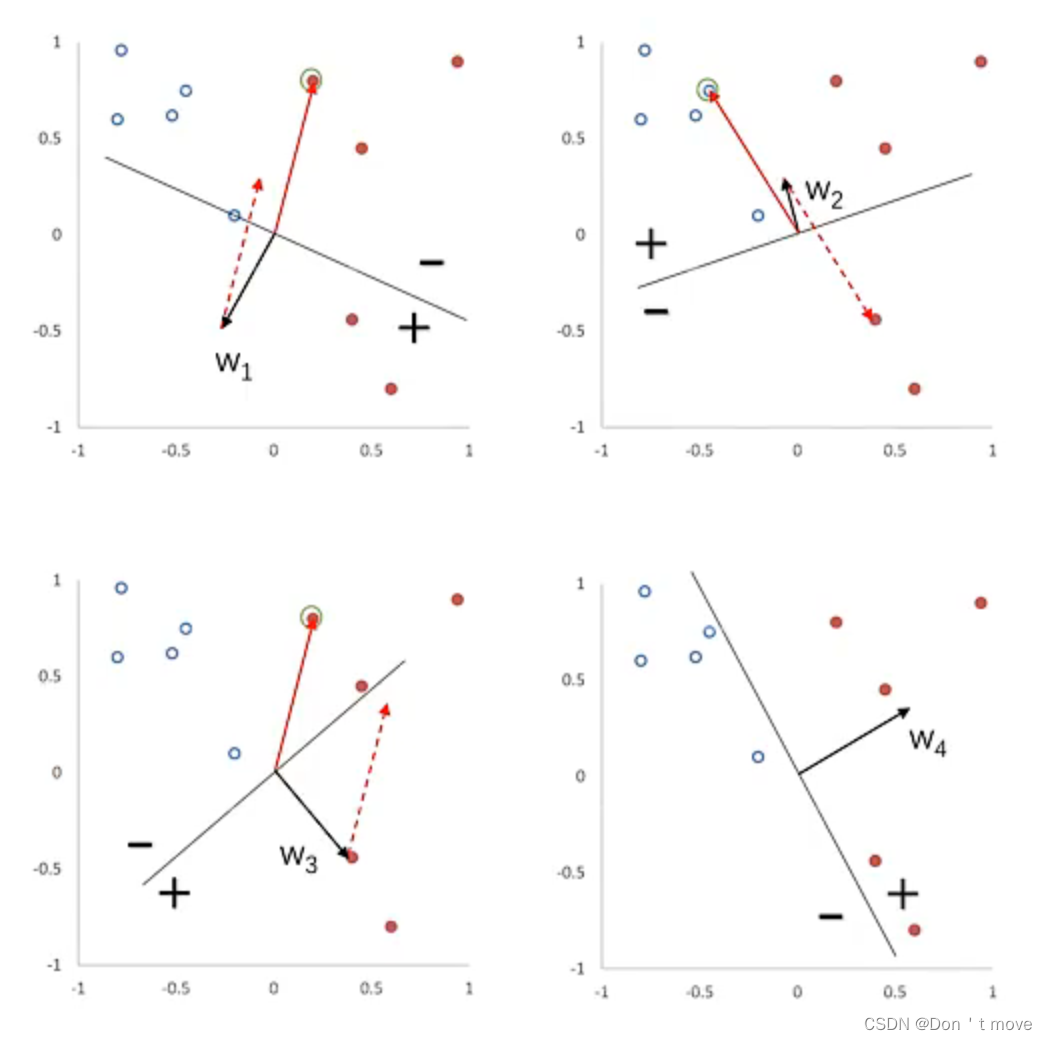
开始先随机初始化一个参数$w_1$，分界面为$w_1^{T}x=0$，此时，感知器预测的正例为$y{w}_1^{T}x>0$、负例为$y{w}_1^{T}x<0$，直观上来看，从分界线到参数$w_1$所在一侧为正例，另一侧为负例，如上图中左上所示。从中随机挑选一个样本，假如取到了正例样本但却被分为负例，则更新参数$w_2=w_1+yx$，其中由于随机的样本是正例，也就是$y=1$，则$w_2=w_1+x$，变成如上图右上所示。同样的操作，经过四次后变为右下所示的图，完成参数学习。

收敛性

感知器的收敛性是指给定训练集$\mathcal{D}=\{(x^{(n)},y^{(n)}){\}}_{n=1}^N$，令R是训练集中最大的特征向量的模，即$R=\underset{n}{\max }\parallel x^{(n)}\parallel$ 。如果训练集$\mathcal{D}$线性可分，两类感知器的参数学习算法权重更新次数不超过$\frac{R^2}{{\gamma }^2}$。其中$\gamma$表示一个趋向于零的很小的数，衡量样本中正负例的分离程度，$\gamma$越大说明样本中两例分离越大反之越小。
也就是说对于线性可分的数据集来说，感知器能够保证在有限的更新步骤当中找到这个分界面。
收敛性证明：
对于感知器来说，权重向量的更新方式为：
$$\begin{array}{rl}{w}_k& =w_{k-1}+y^{(k)}{x}^{(k)}\\ & =w_{k-2}+y^{(k-1)}{x}^{(k-1)}+y^{(k)}{x}^{(k)}\end{array}$$
则在第K次更新时的感知器的权重向量为：
$$w_k=\sum _{k=1}^K{y}^{(k)}{x}^{(k)}$$
则：
$$\begin{array}{rl}\parallel w_k{\parallel }^2& =\parallel w_{k-1}+y^{(k)}{x}^{(k)}{\parallel }^2\\ & =\parallel w_{k-1}{\parallel }^2+\parallel y^{(k)}{x}^{(k)}{\parallel }^2+2w_{k-1}^T{y}^{(k)}{x}^{(k)}\end{array}$$
上式中，由于只有遇到判错才会更新，因此$2w_{k-1}^T{y}^{(k)}{x}^{(k)}<0$。此外，$y^{(k)}=\pm 1$所以式子中$\parallel y^{(k)}{x}^{(k)}{\parallel }^2=\parallel x^{(k)}{\parallel }^2$。式子中的正数项：
$$\begin{array}{rl}\parallel w_{k-1}{\parallel }^2+\parallel y^{(k)}{x}^{(k)}{\parallel }^2& =\parallel w_{k-1}{\parallel }^2+\parallel x^{(k)}{\parallel }^2\\ & \le \parallel w_{k-1}{\parallel }^2+R^2\\ & \le \parallel w_{k-2}{\parallel }^2+2R^2\\ & \le K{R}^2\end{array}$$
加上最后的小于0的项后上式仍然成立，因此可得$\parallel w_k{\parallel }^2\le K{R}^2$。
接下来，设$w^{\ast }$为最优分界面对应的参数，由于$w$的模与分类是无关的，只需要考虑正负号，因此约定$\parallel w^{\ast }{\parallel }^2=1$，同时有公式向量模的内积大于向量内积的模，因此：
$$\begin{array}{rl}\parallel w_k{\parallel }^2& =\parallel w^{\ast }{\parallel }^2\parallel w_k{\parallel }^2\\ & \ge \parallel w^{\ast }{w}_k{\parallel }^2\\ & =\parallel \sum _{k=1}^K{w^{\ast }}^T{y}^{(k)}{x}^{(k)}{\parallel }^2\end{array}$$
因为$w^{\ast }$是最优的参数，因此上式是正确分类，也就是${w^{\ast }}^{T}yx$一定大于零。假设$\gamma \to 0$，则：
$$\begin{array}{rl}\parallel w_k{\parallel }^2& \ge K^2{\gamma }^2\end{array}$$
综上所述，得到：
$$K^2{\gamma }^2\le \parallel w_k{\parallel }^2\le K{R}^2$$
则有：
$$\begin{array}{rl}{K}^2{\gamma }^2& \le K{R}^2\\ K{\gamma }^2& \le R^2\\ K& \le \frac{R^2}{{\gamma }^2}\end{array}$$