一、题目
1、题目描述
2、输入输出
2.1输入
2.2输出
3、原题链接
1879D - Sum of XOR Functions
二、解题报告
1、思路分析
朴素暴力O(N^2),考虑优化
由于要求的是异或值乘长度,那么我们可以按位考虑每一位异或值的贡献
我们枚举每一位
每次遍历一遍前缀和数组,哈希表记录前缀和出现次数cnt[]和出现下标之和sum[]
那么我们当前遍历到的前缀和第k位为j,我们其贡献就是(cnt[j ^ 1] * i - sum[j ^ 1]) * (1 << k)
也是比较典的位运算技巧
2、复杂度
时间复杂度: O(NlogU)空间复杂度:O(NlogU)
3、代码详解
#include <bits/stdc++.h>
using i64 = long long;
using i128 = __int128;
using PII = std::pair<int, int>;
std::ostream& operator<< (std::ostream& out, i128 x) {
std::string s;
while (x) s += ((x % 10) ^ 48), x /= 10;
std::reverse(s.begin(), s.end());
return out << s;
}
void solve() {
const int P = 998244353;
int N;
i64 res = 0;
std::cin >> N;
std::vector<int> nums(N + 1);
for (int i = 1; i <= N; i ++ ) std::cin >> nums[i], nums[i] ^= nums[i - 1];
for (int k = 29; ~k; k -- ) {
std::vector<std::array<i64, 2>> st(2);
st[0][0] = 1;
for (int i = 1; i <= N; i ++ ) {
res = (res + ((st[(nums[i] >> k & 1) ^ 1][0] * i - st[(nums[i] >> k & 1) ^ 1][1]) % P << k)) % P;
st[nums[i] >> k & 1][0] ++, st[nums[i] >> k & 1][1] += i;
}
}
std::cout << res;
}
int main(int argc, char** argv) {
std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);
int _ = 1;
// std::cin >> _;
while (_ --)
solve();
return 0;
}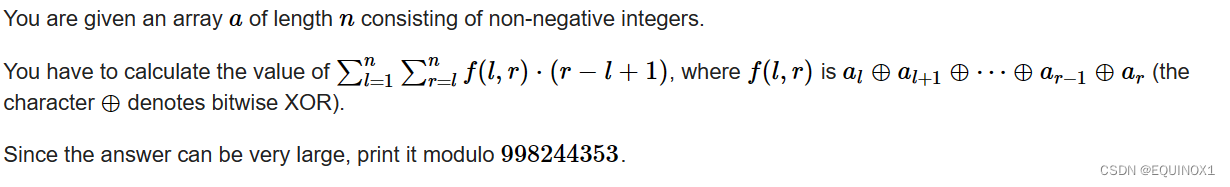


![[Shell编程学习路线]--shell中重定向和管道符(详细介绍)](https://img-blog.csdnimg.cn/direct/fc5439c2b4bb4e23aad2071709574fba.png)