激活函数（Activation Function）是一种添加到人工神经网络中的函数，旨在帮助网络学习数据中的复杂模式。在神经元中，输入的input经过一系列加权求和后作用于另一个函数，这个函数就是这里的激活函数。

1. 为什么需要激活函数

因为神经网络中每一层的输入输出都是一个线性求和的过程，下一层的输出只是承接了上一层输入函数的线性变换，所以如果没有激活函数，那么无论你构造的神经网络多么复杂，有多少层，最后的输出都是输入的线性组合，纯粹的线性组合并不能够解决更为复杂的问题。而引入激活函数之后，我们会发现常见的激活函数都是非线性的，因此也会给神经元引入非线性元素，使得神经网络可以逼近其他的任何非线性函数，这样可以使得神经网络应用到更多非线性模型中。

2. 常见激活函数

（1）Sigmoid函数

取值范围为(0,1)，它可以将一个实数映射到(0,1)的区间，可以用来做二分类。


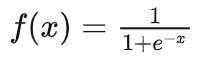
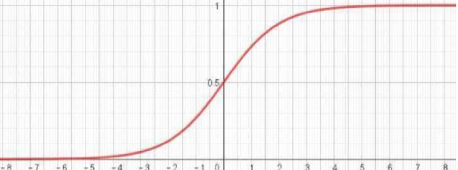
使用范围：
①Sigmoid 函数的输出范围是 0 到 1。由于输出值限定在 0 到1，因此它对每个神经元的输出进行了归一化；

②用于将预测概率作为输出的模型。由于概率的取值范围是 0 到 1，因此 Sigmoid 函数非常合适；
不足之处：

在趋近0/1附近易梯度消失；

不以零为中心：Sigmoid 输出不以零为中心的,，输出恒大于0，非零中心化的输出会使得其下一层的神经元的输入发生偏置偏移（Bias Shift），并进一步使得梯度下降的收敛速度变慢。
计算成本高昂：exp() 函数与其他非线性激活函数相比，计算成本高昂，计算机运行起来速度较慢。

（2）Tanh函数

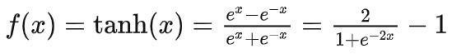
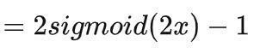
优点：
输出是0均值；
缺点：
依旧在两端存在“梯度消失”；
注意：在一般的二元分类问题中，tanh 函数用于隐藏层，而 sigmoid 函数用于输出层，但这并不是固定的，需要根据特定问题进行调整。

（3）ReLU函数

优点：
①当输入为正时，导数为1，一定程度上改善了梯度消失问题，加速梯度下降的收敛速度；
②计算速度快得多。ReLU 函数中只存在线性关系，因此它的计算速度比 sigmoid 和 tanh 更快。
③被认为具有生物学合理性（Biological Plausibility）,比如单侧抑制、宽兴奋边界（即兴奋程度可以非常高）
缺点：
①Dead ReLU问题，当输入为负时，ReLU 完全失效，在正向传播过程中，这不是问题。有些区域很敏感，有些则不敏感。但是在反向传播过程中，如果输入负数，则梯度将完全为零；

②不以零为中心：和 Sigmoid 激活函数类似，ReLU 函数的输出不以零为中心，ReLU 函数的输出为 0 或正数,给后一层的神经网络引入偏置偏移，会影响梯度下降的效率。

（4）LeakyReLU

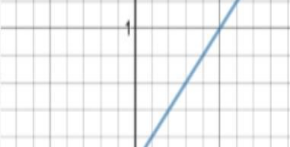
为什么使用Leaky ReLU会比ReLU效果要好呢？
① Leaky ReLU 通过把 x 的非常小的线性分量给予负输入（0.01x）来调整负值的零梯度（zero gradients）问题，当 x < 0 时，它得到 0.1 的正梯度。该函数一定程度上缓解了 dead ReLU 问题，

② leak 有助于扩大 ReLU 函数的范围，通常 a 的值为 0.01 左右；

③ Leaky ReLU 的函数范围是（负无穷到正无穷）

尽管Leaky ReLU具备 ReLU 激活函数的所有特征（如计算高效、快速收敛、在正区域内不会饱和），但并不能完全证明在实际操作中Leaky ReLU 总是比 ReLU 更好。

本节完！