🌈个人主页: 鑫宝Code
🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础
💫个人格言: "如无必要,勿增实体"

文章目录
- 解码拜占庭将军问题:区块链共识机制的哲学基石
- 引言
- 一、拜占庭将军问题概述
- 1.1 定义
- 1.2 关键要素
- 二、问题的复杂性
- 2.1 通信不确定性
- 2.2 叛徒的存在
- 2.3 异步通信的挑战
- 三、解决方案探索
- 3.1 实数口令法
- 3.2 Byzantine Fault Tolerance (BFT)算法
- 3.3 共识机制的兴起
- 四、拜占庭将军问题与区块链的结合
- 4.1 区块链共识的必要性
- 4.2 PoW在比特币中的应用
- 4.3 区块链共识机制的多样性
- 五、挑战与未来展望
- 5.1 扩展性与效率
- 5.2 环境可持续性
- 5.3 法规与合规性
- 结论
解码拜占庭将军问题:区块链共识机制的哲学基石
引言
拜占庭将军问题,一个由Leslie Lamport于1982年提出的经典分布式系统理论问题,是现代加密货币与区块链技术背后的哲学基础。这一理论模型不仅深刻地影响了计算机科学领域,还成为了构建去中心化信任体系的关键灵感来源。本文将深入剖析拜占庭将军问题的本质、解决方案及其对区块链共识机制的深远影响,为读者揭示这一抽象理论的现实应用价值。
一、拜占庭将军问题概述

1.1 定义
拜占庭将军问题描述了一个军事指挥困境:
一组拜占庭将军分别各率领一支军队共同围困一座城市。为了简化问题,将各支军队的行动策略限定为进攻或撤离两种。因为部分军队进攻部分军队撤离可能会造成灾难性后果,因此各位将军必须通过投票来达成一致策略,即所有军队一起进攻或所有军队一起撤离。因为各位将军分处城市不同方向,他们只能通过信使互相联系。在投票过程中每位将军都将自己投票给进攻还是撤退的信息通过信使分别通知其他所有将军,这样一来每位将军根据自己的投票和其他所有将军送来的信息就可以知道共同的投票结果而决定行动策略。
1.2 关键要素
- 将军:代表分布式系统中的各个节点。
- 信使:信息传递渠道,对应于网络中的消息传输。
- 忠诚与背叛:忠诚将军遵循协议,背叛将军则可能发送错误信息。
- 一致性目标:所有忠诚将军必须达成一致的决策(进攻或撤退)。
系统的问题在于,可能将军中出现叛徒,他们不仅可能向较为糟糕的策略投票,还可能选择性地发送投票信息。假设有9位将军投票,其中1名叛徒。8名忠诚的将军中出现了4人投进攻,4人投撤离的情况。这时候叛徒可能故意给4名投进攻的将领送信表示投票进攻,而给4名投撤离的将领送信表示投撤离。这样一来在4名投进攻的将领看来,投票结果是5人投进攻,从而发起进攻;而在4名投撤离的将军看来则是5人投撤离。这样各支军队的一致协同就遭到了破坏。
由于将军之间需要通过信使通讯,叛变将军可能通过伪造信件来以其他将军的身份发送假投票。而即使在保证所有将军忠诚的情况下,也不能排除信使被敌人截杀,甚至被敌人间谍替换等情况。因此很难通过保证人员可靠性及通讯可靠性来解决问题。
假使那些忠诚(或是没有出错)的将军仍然能通过多数决定来决定他们的战略,便称达到了拜占庭容错。在此,票都会有一个默认值,若消息(票)没有被收到,则使用此默认值来投票。
上述的故事映射到计算机系统里,将军便成了计算机,而信差就是通信系统。虽然上述的问题涉及了电子化的决策支持与信息安全,却没办法单纯的用密码学与数字签名来解决。因为电路错误仍可能影响整个加密过程,这不是密码学与数字签名算法在解决的问题。因此计算机就有可能将错误的结果提交去,亦可能导致错误的决策。
二、问题的复杂性
2.1 通信不确定性
在分布式系统中,消息可能丢失、延迟、重复或被篡改,这些都增加了达成一致的难度。
2.2 叛徒的存在
即使只有一个背叛者,也足以破坏整个系统的协调性,因为其他将军无法确定哪些信息是可靠的。
2.3 异步通信的挑战
在异步系统中,没有统一的时间参考点,判断一个节点是否已经“沉默”变得尤为困难。
三、解决方案探索
3.1 实数口令法
Lamport等人最初提出的解决方案之一,通过引入口令的真伪检测机制来排除错误指令,但这要求提前共享秘密信息。
3.2 Byzantine Fault Tolerance (BFT)算法
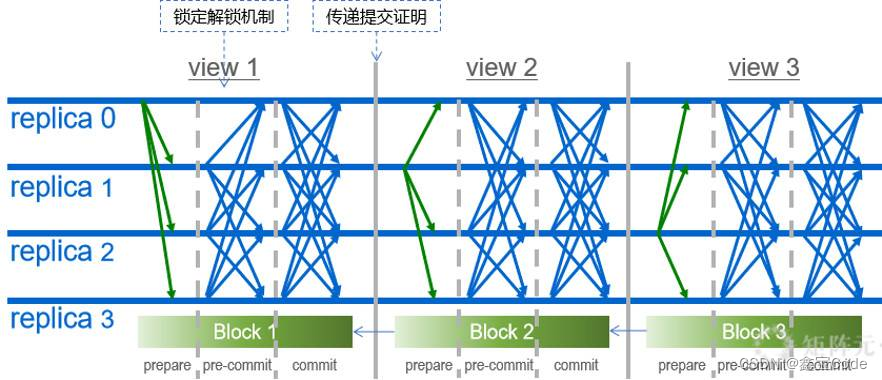
后来发展出的一系列算法,如PBFT(实用拜占庭容错算法),能够在部分节点故障情况下保证系统正常运行,但对网络带宽和延迟有较高要求。
3.3 共识机制的兴起
- Proof of Work (PoW):比特币采用的机制,通过工作量证明保证信息的真实性,但能耗高。
- Proof of Stake (PoS):基于持有代币量来决定决策权,更加节能,但面临不同形式的攻击风险。
- Delegated Proof of Stake (DPoS):通过代理投票减少直接参与决策的节点,提高效率,但仍需解决权力集中问题。
四、拜占庭将军问题与区块链的结合

4.1 区块链共识的必要性
在去中心化的区块链网络中,确保所有节点对交易历史达成一致,防止双花等攻击,是核心挑战之一。
4.2 PoW在比特币中的应用
比特币利用PoW机制,通过竞争记账来确保网络的稳定性和安全性,体现了拜占庭将军问题的解决思路。
4.3 区块链共识机制的多样性
随着技术的发展,各种共识算法的提出,如Casper FFG(以太坊2.0的PoS机制)和Tendermint(Cosmos使用的BFT变体),都是对拜占庭将军问题解决方案的创新与拓展。
五、挑战与未来展望
5.1 扩展性与效率
当前的共识机制在处理大规模交易时仍存在局限,提高系统吞吐量而不牺牲去中心化和安全性是未来的重要方向。
5.2 环境可持续性
PoW的巨大能源消耗引人关注,寻求更加环保的共识机制,如PoS,成为了行业共识。
5.3 法规与合规性
随着区块链技术的普及,如何在确保拜占庭容错的同时,满足全球各地的法规要求,也是未来发展中的一大挑战。
结论
拜占庭将军问题不仅是分布式系统设计中的一道智力难关,更是驱动区块链技术不断迭代创新的哲学动力。从古典理论到现代应用,它见证了人类对于信任机制的深刻理解和不懈追求。随着技术的不断进步,我们有理由相信,未来将会涌现更多高效、安全、环保的共识机制,持续推动区块链世界向前发展,构建一个更加透明、可信的数字经济时代。