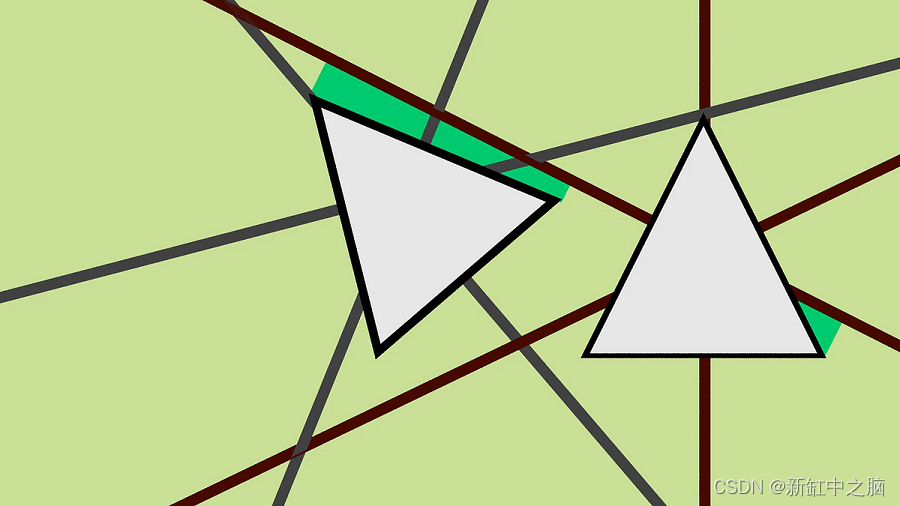
分离轴定理（Seperating Axis Theorem）是一种确定两个凸多边形是否相交的方法。该算法还可用于查找最小穿透向量，这对于物理模拟和许多其他应用非常有用。SAT 是一种快速通用算法，可以消除对每个形状类型对进行碰撞检测代码的需求，从而减少代码和维护。

NSDT工具推荐： Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割 

1、凸度

如前所述，SAT 是一种确定两个凸形是否相交的方法。如果任何穿过该形状的线只相交两次，则该形状被认为是凸形（convex）。如果一条线可以穿过该形状并相交两次以上，则该形状为非凸形或凹形（concave）。有关更正式的定义，请参阅 Wiki 的定义和 MathWorld 的定义。

让我们看一些例子：

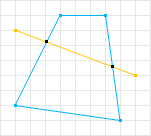
图1：凸形状

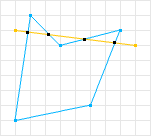
图2：非凸形状

第一个形状被认为是凸的，因为不存在可以穿过该形状并相交超过两次的线。第二个形状不是凸的，因为确实存在相交超过两次的线。

SAT 只能处理凸形状，但这是可以的，因为非凸形状可以用凸形状的组合来表示，这被称为凸分解（convex decomposition）。因此，如果我们采用图 2 中的非凸形状并执行凸分解，我们可以得到两个凸形状。然后我们可以测试每个凸形状以确定整个形状的碰撞。

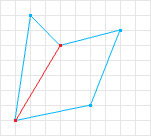
图3：凸分解

2、投影

SAT 使用的下一个概念是投影（projection）。想象一下，你有一个光源，它的光线都是平行的。如果你把这束光照射到一个物体上，它会在表面上产生阴影。阴影是三维物体的二维投影。二维物体的投影是一维“阴影”。

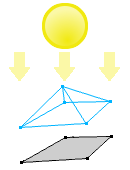
图 4：投影（或阴影）

3、SAT算法

SAT 指出：“如果两个凸面物体不相交，则存在一个轴，物体的投影不会在该轴上重叠。”

3.1 不相交

首先让我们讨论一下 SAT 如何确定两个形状不相交。在图 5 中，我们知道这两个形状不相交。在它们之间画一条线来说明这一点。

图 5：两个分离的凸形

如果我们选择图 5 中两个形状之间的垂直线，并将形状投影到该线上，我们可以看到它们的投影没有重叠。形状投影（阴影）不重叠的线称为分离轴。图 6 中的深灰色线是分离轴，相应的彩色线是形状在分离轴上的投影。请注意，图 6 中的投影没有重叠，因此根据 SAT，形状没有相交。

图 6：两个分离的凸形及其各自的投影

SAT 可能会测试多个轴的重叠情况，但是，如果投影不重叠的第一个轴，算法可以立即退出，并确定形状不相交。由于这种提前退出，SAT 非常适合具有许多对象但很少发生碰撞的应用程序（游戏、模拟等）。

为了进一步解释，请查看以下伪代码：

Axis[] axes = // get the axes to test;
// loop over the axes
for (int i = 0; i < axes.length; i++) {
  Axis axis = axes[i];
  // project both shapes onto the axis
  Projection p1 = shape1.project(axis);
  Projection p2 = shape2.project(axis);
  // do the projections overlap?
  if (!p1.overlap(p2)) {
    // then we can guarantee that the shapes do not overlap
    return false;
  }
}

3.2 相交

如果对于所有轴，形状的投影都重叠，那么我们可以得出结论，形状是相交的。图 7 展示了在多个轴上测试的两个凸形状。形状在这些轴上的投影全部重叠，因此我们可以得出结论，形状是相交的。

图 7：两个凸形相交

必须测试所有轴的重叠度才能确定相交。上面修改后的代码为：

Axis[] axes = // get the axes to test;
// loop over the axes
for (int i = 0; i < axes.length; i++) {
  Axis axis = axes[i];
  // project both shapes onto the axis
  Projection p1 = shape1.project(axis);
  Projection p2 = shape2.project(axis);
  // do the projections overlap?
  if (!p1.overlap(p2)) {
    // then we can guarantee that the shapes do not overlap
    return false;
  }
}
// if we get here then we know that every axis had overlap on it
// so we can guarantee an intersection
return true;

3、获取分离轴

我在实施此算法时遇到的第一个问题是如何知道要测试哪些轴？这实际上非常简单：

你必须测试的轴是每个形状边缘的法线。

图 8：边的法线

可以通过翻转坐标并取负一来获得边缘的法线。例如：

Vector[] axes = new Vector[shape.vertices.length];
// loop over the vertices
for (int i = 0; i < shape.vertices.length; i++) {
  // get the current vertex
  Vector p1 = shape.vertices[i];
  // get the next vertex
  Vector p2 = shape.vertices[i + 1 == shape.vertices.length ? 0 : i + 1];
  // subtract the two to get the edge vector
  Vector edge = p1.subtract(p2);
  // get either perpendicular vector
  Vector normal = edge.perp();
  // the perp method is just (x, y) =&gt; (-y, x) or (y, -x)
  axes[i] = normal;
}

在上述方法中，我们返回形状每个边缘的垂直向量。这些向量称为“法线”向量。但是，这些向量并未标准化（不是单位长度）。如果你只需要 SAT 算法的布尔结果，这就足够了，但如果你需要碰撞信息（稍后将在 MTV 部分讨论），则需要标准化这些向量（请参阅将形状投影到轴上部分）。

对每个形状执行此操作以获取要测试的两个轴列表。这样做会将上面的伪代码更改为：

Axis[] axes1 = shape1.getAxes();
Axis[] axes2 = shape2.getAxes();
// loop over the axes1
for (int i = 0; i < axes1.length; i++) {
  Axis axis = axes1[i];
  // project both shapes onto the axis
  Projection p1 = shape1.project(axis);
  Projection p2 = shape2.project(axis);
  // do the projections overlap?
  if (!p1.overlap(p2)) {
    // then we can guarantee that the shapes do not overlap
    return false;
  }
}
// loop over the axes2
for (int i = 0; i < axes2.length; i++) {
  Axis axis = axes2[i];
  // project both shapes onto the axis
  Projection p1 = shape1.project(axis);
  Projection p2 = shape2.project(axis);
  // do the projections overlap?
  if (!p1.overlap(p2)) {
    // then we can guarantee that the shapes do not overlap
    return false;
  }
}
// if we get here then we know that every axis had overlap on it
// so we can guarantee an intersection
return true;

4、将形状投影到轴上

另一件不清楚的事情是如何将形状投影到轴上。将多边形投影到轴上相对简单；循环遍历所有顶点，与轴执行点积并存储最小值和最大值。

double min = axis.dot(shape.vertices[0]);
double max = min;
for (int i = 1; i < shape.vertices.length; i++) {
  // NOTE: the axis must be normalized to get accurate projections
  double p = axis.dot(shape.vertices[i]);
  if (p < min) {
    min = p;
  } else if (p > max) {
    max = p;
  }
}
Projection proj = new Projection(min, max);
return proj;

5、查找 MTV

到目前为止，我们只在两个形状相交时返回 true 或 false。除此之外，SAT 还可以返回最小平移向量 (Minimum Translation Vector)。MTV 是用于将形状推离碰撞的最小幅度向量。如果我们回顾图 7，我们可以看到轴 C 具有最小重叠。该轴和重叠是 MTV，轴是向量部分，重叠是幅度部分。

要确定形状是否相交，我们必须循环遍历两个形状的所有轴，这样我们就可以同时跟踪最小重叠和轴。如果我们修改上面的伪代码以包含这一点，我们可以在形状相交时返回 MTV。

double overlap = // really large value;
Axis smallest = null;
Axis[] axes1 = shape1.getAxes();
Axis[] axes2 = shape2.getAxes();
// loop over the axes1
for (int i = 0; i < axes1.length; i++) {
  Axis axis = axes1[i];
  // project both shapes onto the axis
  Projection p1 = shape1.project(axis);
  Projection p2 = shape2.project(axis);
  // do the projections overlap?
  if (!p1.overlap(p2)) {
    // then we can guarantee that the shapes do not overlap
    return false;
  } else {
    // get the overlap
    double o = p1.getOverlap(p2);
    // check for minimum
    if (o < overlap) {
      // then set this one as the smallest
      overlap = o;
      smallest = axis;
    }
  }
}
// loop over the axes2
for (int i = 0; i < axes2.length; i++) {
  Axis axis = axes2[i];
  // project both shapes onto the axis
  Projection p1 = shape1.project(axis);
  Projection p2 = shape2.project(axis);
  // do the projections overlap?
  if (!p1.overlap(p2)) {
    // then we can guarantee that the shapes do not overlap
    return false;
  } else {
    // get the overlap
    double o = p1.getOverlap(p2);
    // check for minimum
    if (o < overlap) {
      // then set this one as the smallest
      overlap = o;
      smallest = axis;
    }
  }
}
MTV mtv = new MTV(smallest, overlap);
// if we get here then we know that every axis had overlap on it
// so we can guarantee an intersection
return mtv;

6、弯曲形状

我们已经了解了如何使用 SAT 测试多边形，但是像圆形这样的弯曲形状呢？弯曲形状对 SAT 来说是一个问题，因为弯曲形状有无数个分离轴需要测试。解决这个问题的方法是将“圆与圆”和“圆与多边形”测试分开，然后做一些更具体的工作。另一种选择是根本不使用弯曲形状，而是用高顶点数多边形代替它们。第二种选择不需要更改上述伪代码，但我想介绍第一种选择。

让我们首先看看“圆与圆”。通常，你会执行以下操作：

Vector c1 = circle1.getCenter();
Vector c2 = circle2.getCenter();
Vector v = c1.subtract(c2);
if (v.getMagnitude() < circle1.getRadius() + circle2.getRadius()) {
  // then there is an intersection
}
// else there isnt

如果两个圆心之间的距离小于圆半径之和，我们就知道它们相撞了。这个测试实际上是一个类似 SAT 的测试。为了在 SAT 中实现这一点，我们可以执行以下操作：

Vector[] axes = new Vector[1];
if (shape1.isCircle() && shape2.isCircle()) {
  // for two circles there is only one axis test
  axes[0] = shape1.getCenter().subtract(shape2.getCenter);
}
// then all the SAT code from above</pre>

圆形与多边形的问题更大。中心到中心测试以及多边形轴是不够的（事实上，中心到中心测试可以省略）。在这种情况下，您必须包含另一个轴：从多边形上最近的顶点到圆心的轴。可以通过多种方式找到多边形上最近的顶点，公认的解决方案是使用 Voronoi 区域，我不会在这篇文章中讨论。

其他弯曲形状将是一个更大的问题，必须以自己的方式处理。例如，胶囊形状可以分解为一个矩形和两个圆形。

7、包容性

许多开发人员选择忽略的问题之一是包容性。当一个形状包含另一个形状时会发生什么？这个问题通常不是什么大问题，因为大多数应用程序永远不会发生这种情况。首先让我解释一下这个问题以及如何处理它。然后我会解释为什么应该考虑它。

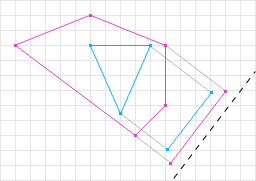
图9：包容性

如果一个形状包含在另一个形状 SAT 中，根据我们目前拥有的伪代码，将返回不正确的 MTV。矢量和幅度部分可能都不正确。图 9 显示返回的重叠不足以将形状移出相交。所以我们需要做的是在重叠测试中检查包含情况。仅从上面的 SAT 代码中获取 if 语句：

if (!p1.overlap(p2)) {
  // then we can guarantee that the shapes do not overlap
  return false;
} else {
  // get the overlap
  double o = p1.getOverlap(p2);
  // check for containment
  if (p1.contains(p2) || p2.contains(p1)) {
    // get the overlap plus the distance from the minimum end points
    double mins = abs(p1.min - p2.min);
    double maxs = abs(p1.max - p2.max);
    // NOTE: depending on which is smaller you may need to
    // negate the separating axis!!
    if (mins < maxs) {
      o += mins;
    } else {
      o += maxs;
    }
  }
  // check for minimum
  if (o < overlap) {
    // then set this one as the smallest
    overlap = o;
    smallest = axis;
  }
}

原因 1：形状有可能处于这种配置类型。如果不处理这种情况，则需要两次或更多次 SAT 迭代来解决碰撞，具体取决于形状的相对大小。

原因 2：如果您计划支持线段与其他形状，则必须这样做，因为在某些情况下重叠可能为零（这是因为线段是无限薄的形状）。

8、其他注意事项

其他一些注意事项：

• 通过不测试平行轴可以减少要测试的轴数。这就是为什么矩形只有两个轴要测试的原因。
• 如果某些形状（如矩形）具有自己的投影和 getAxes 代码，则可以执行得更快，因为矩形不需要测试 4 个轴，而实际上只需要 2 个。
• 最后一个分离轴可用于启动 SAT 的下一次迭代，以便在非相交情况下算法可以是 O(1)。
• 3D 中的 SAT 最终可能会测试很多轴。

---

原文链接：分离轴(SAT)相交检测算法 - BimAnt