原题链接🔗：螺旋矩阵
难度：中等⭐️⭐️

题目

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

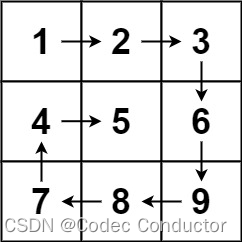
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

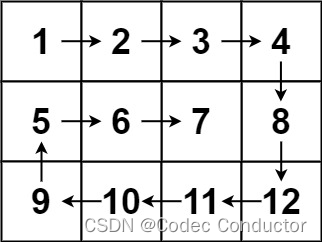
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

提示：
m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 1

题解

四指针遍历法

1. 题解：

这个算法不需要修改原始矩阵。以下是实现这个算法的步骤：

1. 初始化四个边界：top 表示矩阵的顶部边界，bottom 表示底部边界，left 表示左侧边界，right 表示右侧边界。
2. 创建一个空列表 result 用于存储按螺旋顺序排列的元素。
3. 使用一个循环，直到 top 大于 bottom 或 left 大于 right：
   • 从 left 到 right 遍历 top 行，将这些元素添加到 result。
   • 增加 top 的值，缩小顶部边界。
   • 从 top 到 bottom 遍历 right 列，将这些元素添加到 result。
   • 减少 right 的值，缩小右侧边界。
   • 如果 top 小于等于 bottom，从 right 到 left 遍历 bottom 行，将这些元素添加到 result。
   • 减少 bottom 的值，缩小底部边界。
   • 如果 left 小于等于 right，从 bottom 到 top 遍历 left 列，将这些元素添加到 result。
   • 增加 left 的值，缩小左侧边界。
4. 返回 result 列表，它包含了矩阵中所有元素的顺时针螺旋顺序。

2. 复杂度：时间复杂度O(m×n)，因为每个单元格都被填充一次；空间复杂度O(m×n)，用于存储最终的矩阵。
3. 过程：

螺旋矩阵是一种特殊的矩阵，其元素按照螺旋的方式填充，从外圈向内圈逐渐填充，每个元素的值依次递增。

实现过程如下：

1. 首先，函数检查输入矩阵是否为空或其子数组是否为空。如果是，则直接返回一个空的一维数组。

2. 定义四个变量top, bottom, left, right来分别表示矩阵的上边界、下边界、左边界和右边界。

3. 使用一个while循环，当top不大于bottom且left不大于right时，循环继续。这确保了矩阵中至少还有一行或一列可以遍历。

4. 在循环内部，首先从left到right遍历矩阵的顶部行，将这些元素添加到结果数组中，然后top加1。

5. 接着，从top到bottom遍历矩阵的最右列，将这些元素添加到结果数组中，然后right减1。

6. 确保在继续之前，当前的遍历行与上一次的遍历行不同（如果top小于等于bottom），从right到left遍历矩阵的底部行，然后bottom减1。

7. 同样，确保在继续之前，当前的遍历列与上一次的遍历列不同（如果left小于等于right），从bottom到top遍历矩阵的最左列，然后left加1。

8. 函数最后返回包含矩阵所有元素的一维数组，这些元素按照螺旋顺序排列。

main函数中创建了3x3、3x4的两个矩阵，并调用spiralOrder函数来获取螺旋顺序的元素，然后打印这些元素。

4. c++ demo：

#include <iostream>
#include <vector>

std::vector<int> spiralOrder(const std::vector<std::vector<int>>& matrix) {
    if (matrix.empty() || matrix[0].empty()) return {};

    std::vector<int> result;
    int top = 0, bottom = matrix.size() - 1;
    int left = 0, right = matrix[0].size() - 1;

    while (top <= bottom && left <= right) {
        // Traverse from left to right.
        for (int i = left; i <= right; ++i) {
            result.push_back(matrix[top][i]);
        }
        ++top;

        // Traverse downwards.
        for (int i = top; i <= bottom; ++i) {
            result.push_back(matrix[i][right]);
        }
        --right;

        // Make sure we are now on a different row.
        if (top <= bottom) {
            for (int i = right; i >= left; --i) {
                result.push_back(matrix[bottom][i]);
            }
            --bottom;
        }

        // Make sure we are now on a different column.
        if (left <= right) {
            for (int i = bottom; i >= top; --i) {
                result.push_back(matrix[i][left]);
            }
            ++left;
        }
    }

    return result;
}

int main() {
    std::vector<std::vector<int>> matrix = {
        {1, 2, 3},
        {4, 5, 6},
        {7, 8, 9}
    };

    std::vector<int> spiral = spiralOrder(matrix);

    for (int num : spiral) {
        std::cout << num << " ";
    }
    std::cout << std::endl;

    std::vector<std::vector<int>> matrix2 = {
    {1, 2,  3,  4 },
    {5, 6,  7,  8 },
    {9, 10, 11, 12}
    };
    std::vector<int> spiral2 = spiralOrder(matrix2);

    for (int num : spiral2) {
        std::cout << num << " ";
    }
    std::cout << std::endl;

    return 0;
}

• 输出结果：

1 2 3 6 9 8 7 4 5
1 2 3 4 8 12 11 10 9 5 6 7