前言：本篇文章介绍了一下二叉树中的基本知识点，包括二叉树的种类、二叉树的存储方式以及二叉树的深度和广度优先遍历；以及《数据结构与算法》中对于数组的讲解记录，只记录了本前端能看懂的🤓，还有很多知识点是我看不懂的，后端老师请自行探索吧。

一、二叉树

最近一直在刷《代码随想录》二叉树相关的题目，总结一下非常基本的一些知识点

（一）二叉树的种类

1、满二叉树

二叉树上只有度为0和度为2的节点，并且度为0的节点都在同一层，这样的二叉树叫做满二叉树。
就是所有的节点都满满当当的。假设二叉树的深度为k，那么满二叉树的节点数为 2^k -1

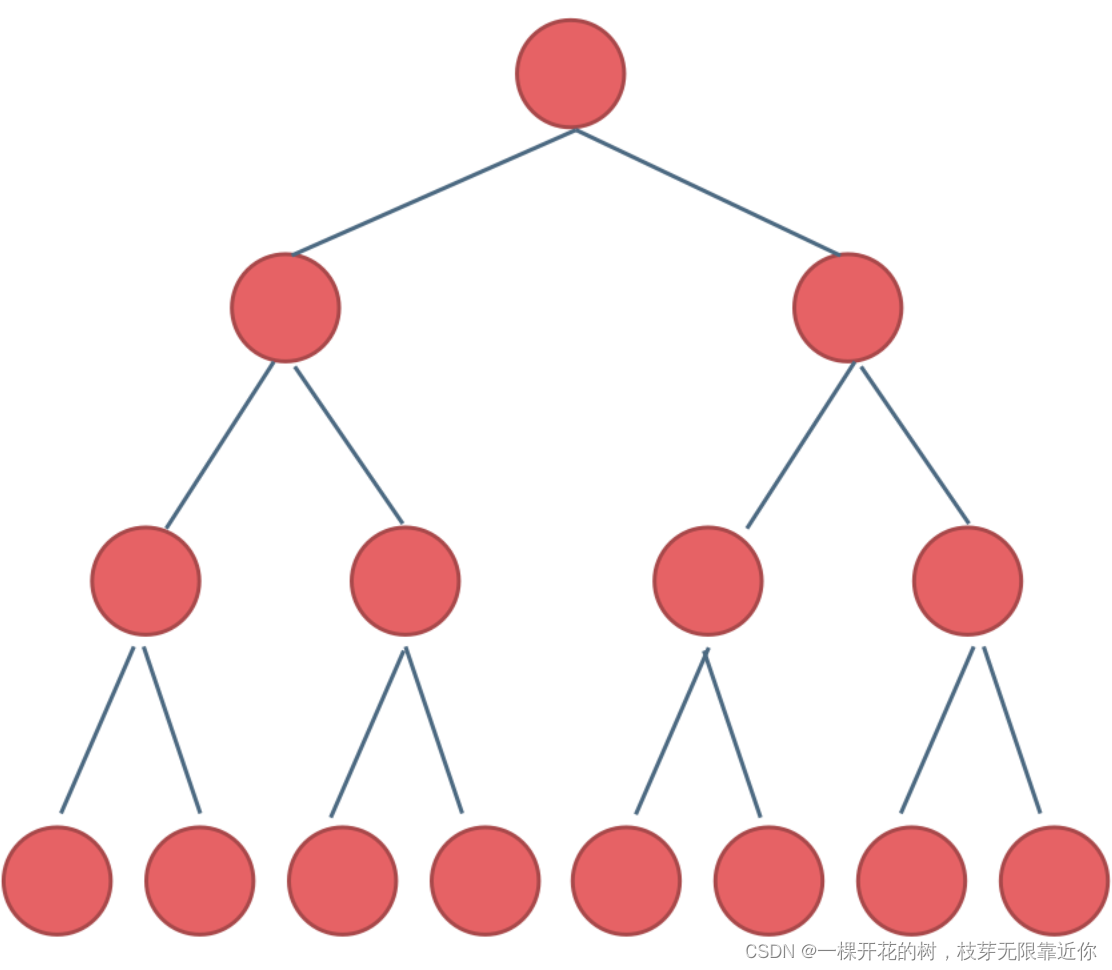
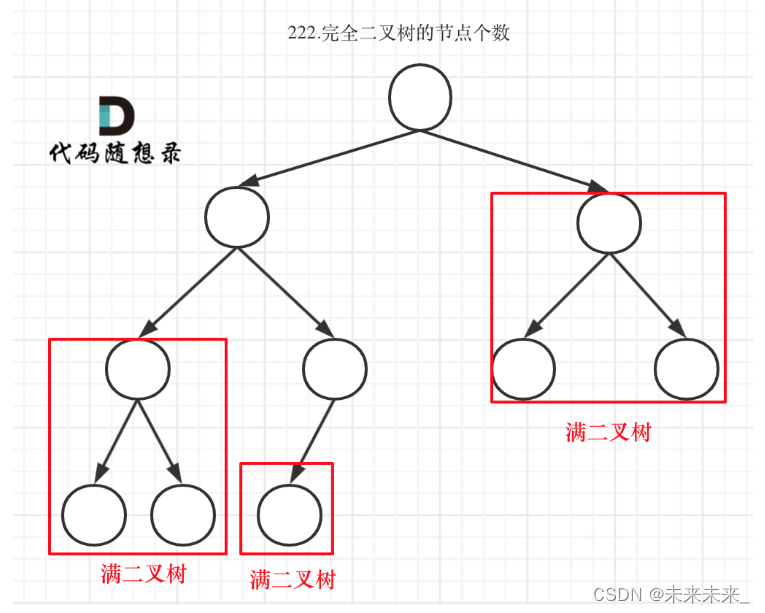
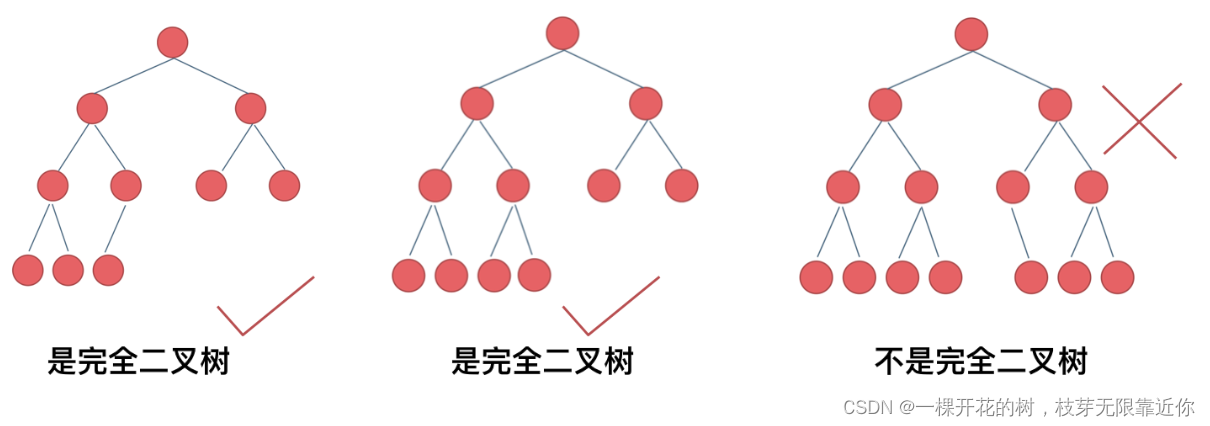
2、完全二叉树

完全二叉树除了最底层没有填满，其他层的节点都是满的。最后一层的节点集中在左侧。

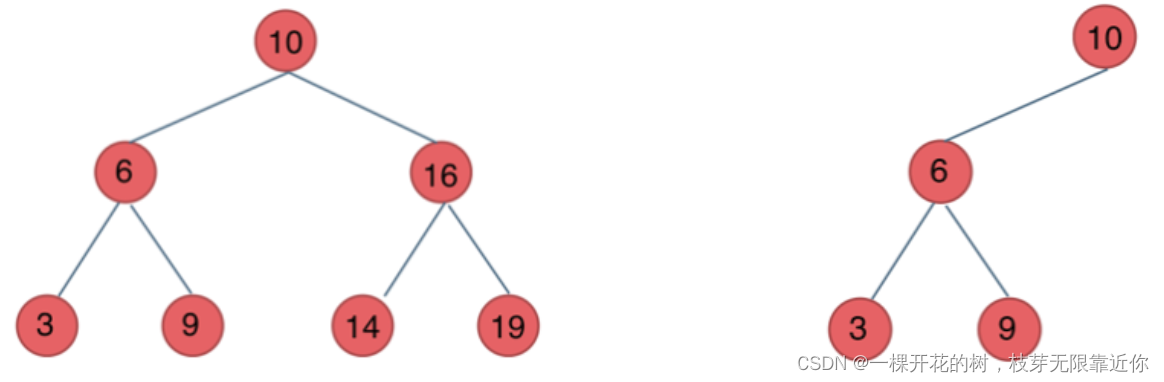
3、二叉搜索树

二叉搜索树是有顺序的树。
对于二叉搜索树的所有节点，如果左子树不为空，那么左子树上所有节点值都小于节点值；如果右子树不为空，那额右子树上所有节点值都大于节点值。

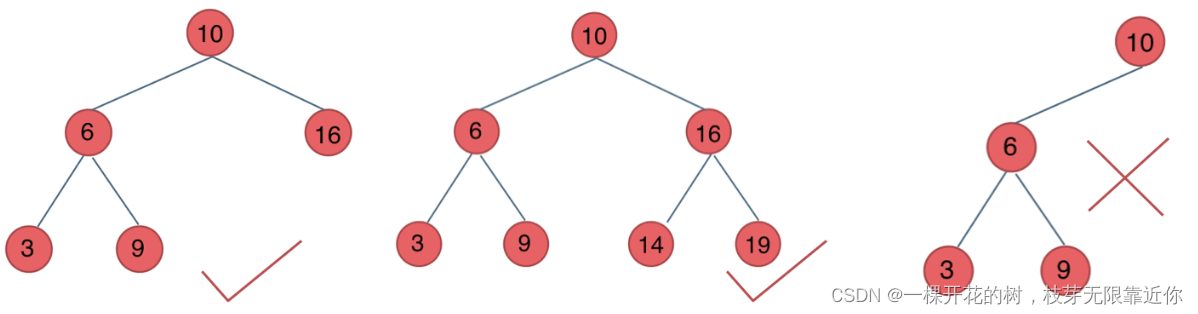
4、平衡二叉树

它是一棵空树，或者左右子树的高度差不超过1

（二）二叉树的存储方式

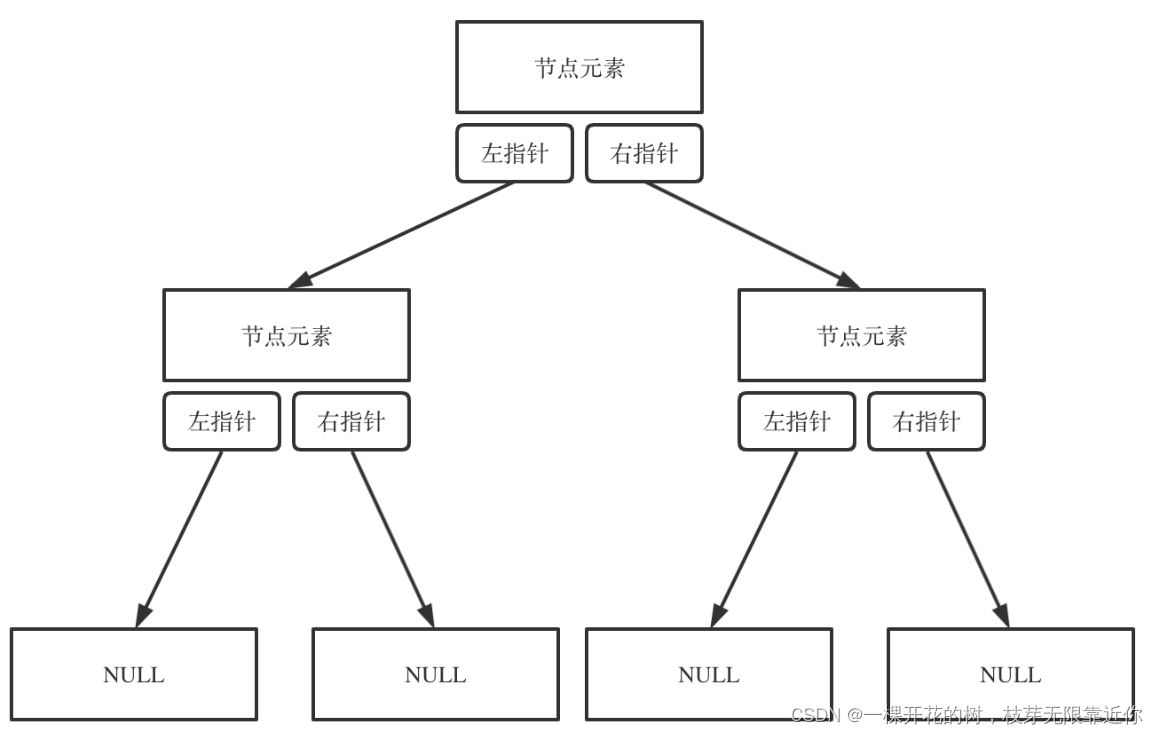
1、使用指针的链式存储

链式存储就是用 TreeNode 这个数据类型存储，相信大家在刷力扣的时候见过很多次了。

3、使用数组的顺序存储

使用数组存储的顺序是按照层序遍历的顺序

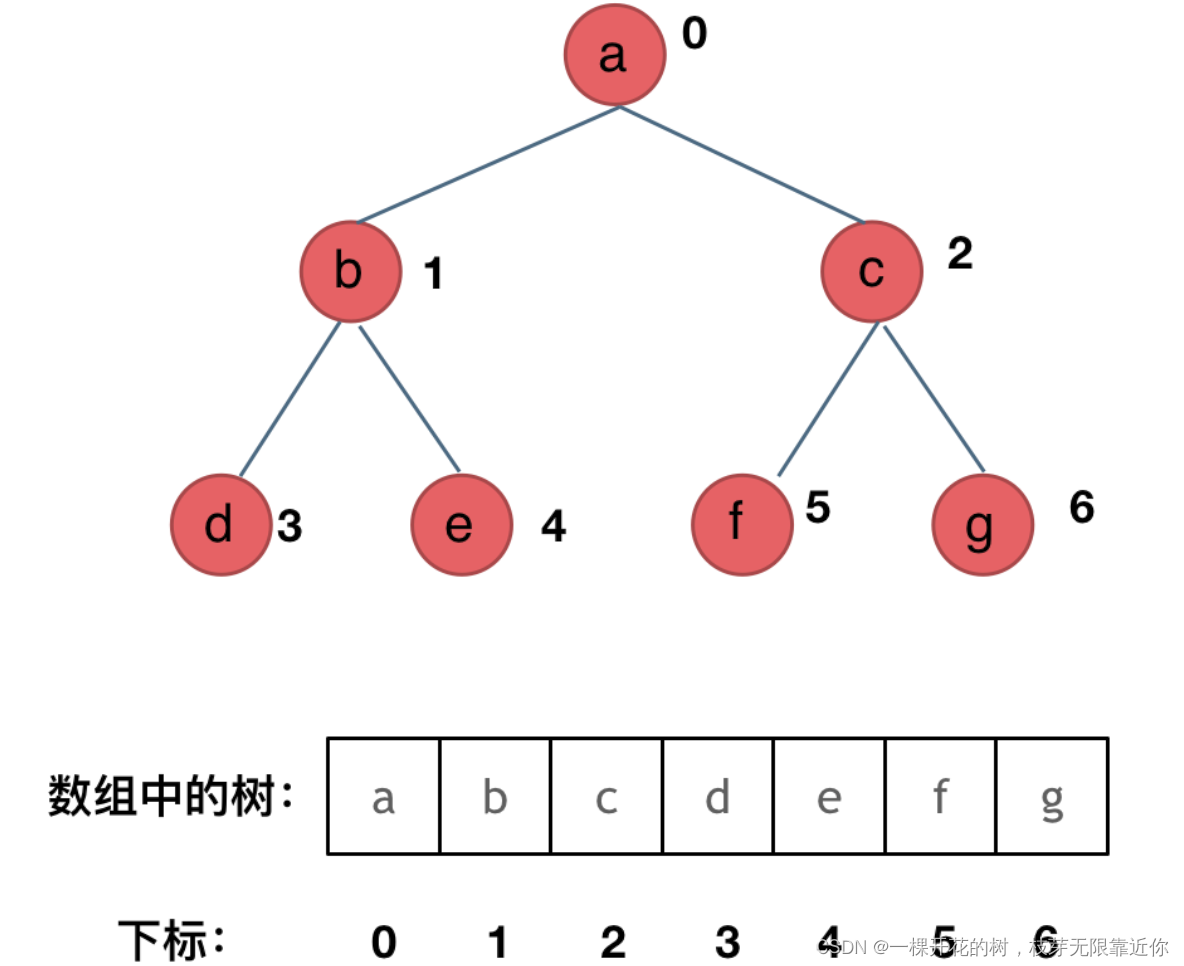
假设节点的索引是 i，那么左节点的索引就是 i*2+1；右节点的索引就是 i*2+2。

（三）二叉树的遍历

神一样的递归三部曲：
1、确定递归的参数和返回值
2、确定递归的终止条件
3、确定递归的单层逻辑

1、深度遍历

深度遍历的前中后序中的前中后，指的是中间节点出现的顺序

（1）前序

就是中左右的顺序
① 递归

const dfs = function (node) {
    if (!node) return;
    // 访问中间节点
    console.log(node);
    dfs(node.left);
    dfs(node.right);
}

② 迭代
前序遍历的访问顺序是 中左右，先访问中节点，使用栈暂存中节点的左右子节点，由于栈是先进后出的，所以应该先加入右节点，后加入左节点

var preorderTraversal = function (root) {
    const ans = [];
    if (!root) return ans;
    const stack = [root];
    while (stack.length) {
        const item = stack.pop();
        ans.push(item.val);
        item.right && stack.push(item.right);
        item.left && stack.push(item.left);
    }
    return ans;
};

（2）中序

顺序是 左中右
① 递归

const dfs = function (node) {
    if (!node) return;
    dfs(node.left);
    // 访问中间节点
    console.log(node);
    dfs(node.right);
}

② 迭代

// 中序遍历 左中右
// 其实递归就是一个模拟的过程
// 要先加左节点就要一直 .left 到达左叶子节点
// 所以要先将路过的节点存到stack里面
// 并且要用指针指向当前节点
var inorderTraversal = function (root) {
    const stack = [];
    const res = [];
    let cur = root;
    while (stack.length || cur) {
        if (cur) {
            stack.push(cur)
            // 一直找 .left
            cur = cur.left;
        } else {
            // 出栈
            const item = stack.pop();
            res.push(item.val);
            cur = item.right;
        }
    }
    return res;
};

（3）后序

顺序是 左右中
① 递归

const dfs = function (node) {
    if (!node) return;
    dfs(node.left);
    dfs(node.right);
    // 访问中间节点
    console.log(node);
}

② 迭代
上面的前序遍历的迭代实现的是 中左右，后序遍历顺序是 左右中，那么只需要先把前序变成 中右左，然后再翻转最后得到的数组就可以了

var postorderTraversal = function (root) {
    const ans = [];
    if (!root) return ans;
    const stack = [root];
    while(stack.length){
        const cur = stack.pop();
        ans.push(cur.val);
        cur.left && stack.push(cur.left);
        cur.right && stack.push(cur.right);
    }
    return ans.reverse();
};

2、广度优先遍历

就是层序遍历，使用队列或者栈暂存

 // 使用队列保存每一层的节点
var levelOrder = function(root) {
    const ans = [];
    if(!root) return ans;
    const queue = [root];
    while(queue.length){
        const len = queue.length;
        for(let i=0;i<len;i++){
            const item = queue.shift();
            ans.push(item.val);
            item.left && queue.push(item.left);
            item.right && queue.push(item.right);
        }
    }
    return ans;
};

二、数组

这一节是《数据结构与算法之美》基础课的第一讲
数组是数据结构中最基本的概念，是我们每天都在用的数据结构，对于这个我们自认为简单又熟悉的数据结构，却有一个深刻而陌生的问题：
数组为什么从0开始编号呢？
下面就通过这一章的学习来解答这个问题，让我们对数组更亲切熟悉吧。

（一）基础概念

虽然大家对数组很熟悉，但是还是有必要用学术性的语言定义一下数组
数组（Array）是一种线性表数据结构。它用一组连续的内存空间，来存储一组具有相同类型的数据。
其中涉及到的线性表概念解释一下

1、线性表

线性表就是在排列上排成一条线的结构，它只有前后两个方向，线性表的种类：数组、列表、队列、栈等等

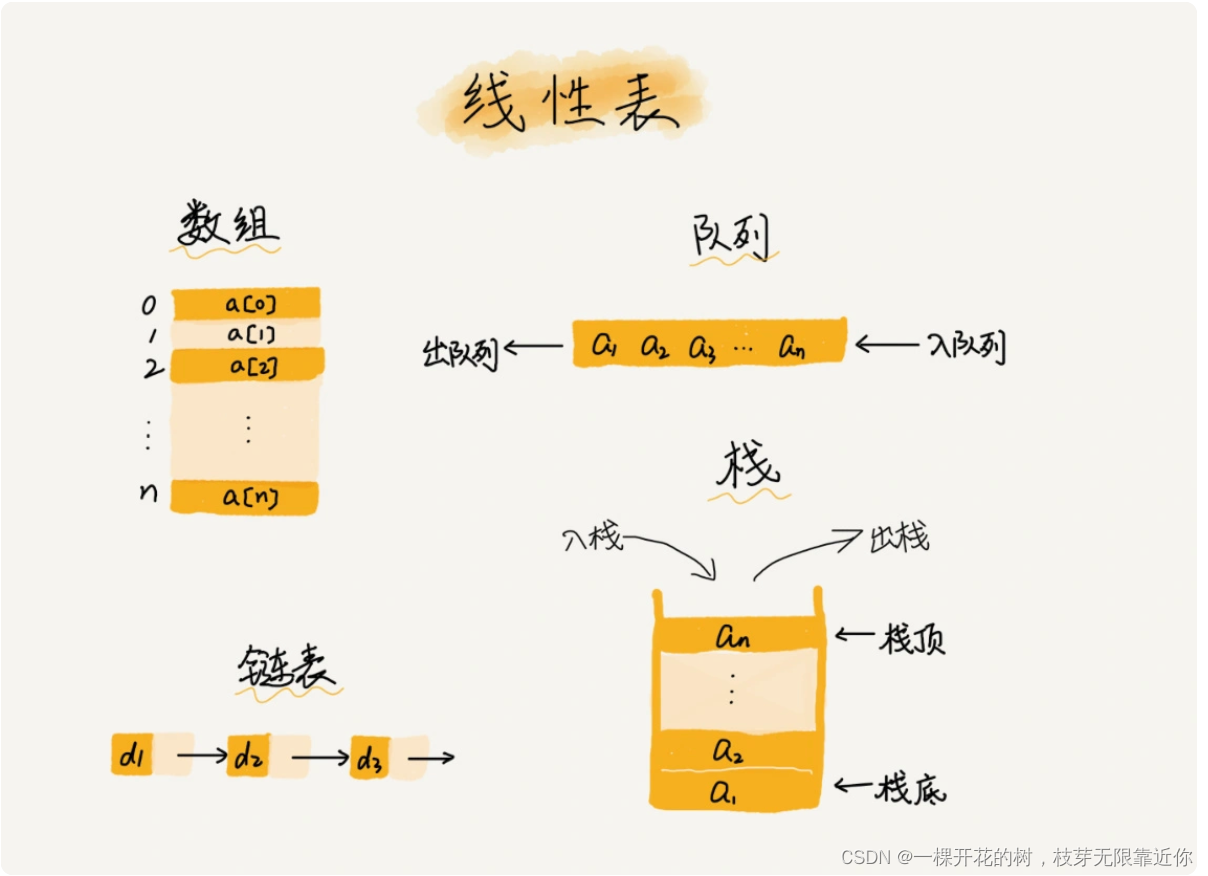
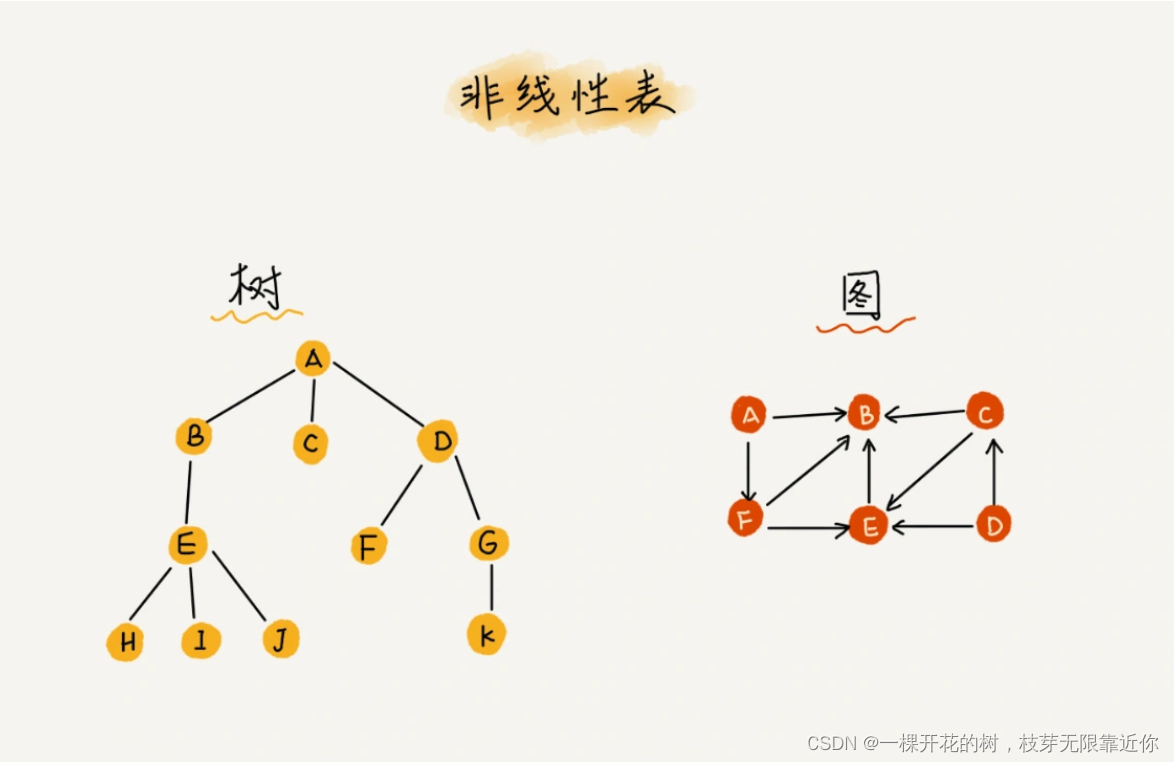
2、非线性表

就是数据排列不是线性的数据结果，数据不是简单的前后关系，比如二叉树、图、堆等

（三）数组的特性

1、随机访问

由于数组是在连续空间上存储的相同数据类型的数据，这种特性使得数组具有 随机访问 的能力，也就是可以根据数组的下标随机访问数组元素。那么这个特异功能是怎么实现的呢？
我们以一个长度为10的数组举例，计算机会为这个数组开辟长度为10的空间，假设分配的内存空间是 1000 ~ 1039，其中内存块的首地址 base_address 是1000

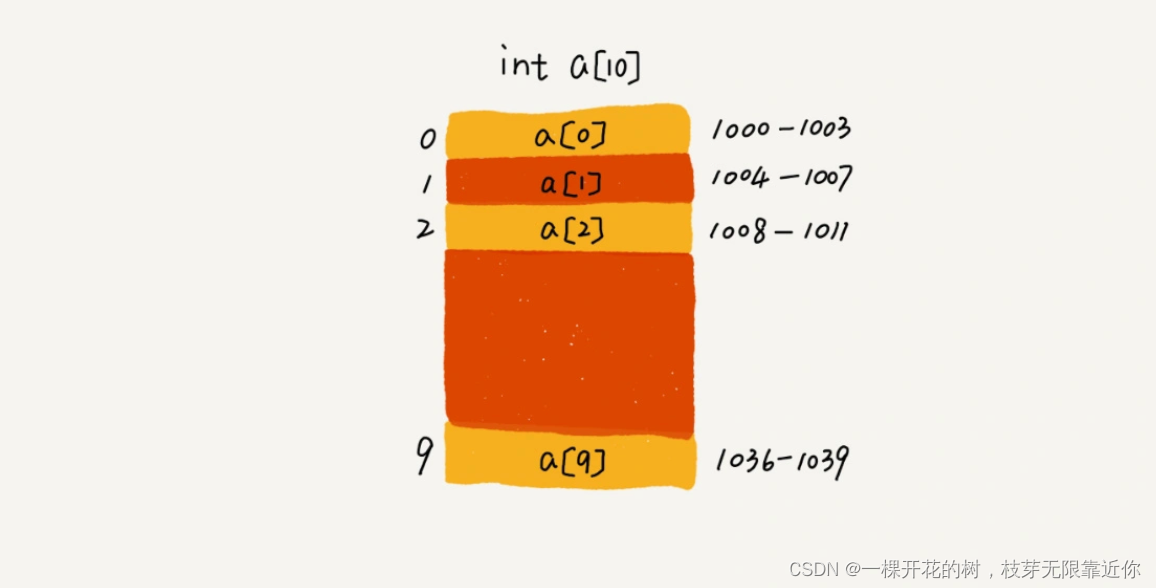
计算机会给每个内存单元分配地址，计算机通过寻找内存地址来寻找对应的数据，当计算机需要随机访问数组中的某个元素的时候，就会通过下面的寻址公式查找对应位置的数据

a[i]_address = base_address + i * data_type_size

其中 data_type_size 表示内存空间大小，对于我们的例子 int 类型来说，就是4个字节。
由于这种根据寻址公式查找数据的机制，数组可以支持时间复杂度为 O(1) 的随机访问。

2、插入删除速度慢

由于连续存储数据的这种机制，数组的插入和删除操作的速度会比较慢。

• 插入操作
  先分析一下插入操作，要插入一个元素，就必须要把这个元素后面的元素都往后搬运一位，然后把元素放在指定位置。
  这样的时间复杂是多少呢？
  时间复杂度取决于要进行多少次数据操作。最好情况下，我们在数组的最后插入元素，那么不需要搬运其他元素，时间复杂度为 O(1)，所以最好时间复杂度就是 O(1)；最坏情况下，我们在数组的开头插入元素，所有的元素都需要往后搬运一位，最坏情况时间复杂度就是 O(n)。又由于插入的位置从 1 ~ n 的概率都是 1/n，所以平均时间复杂度是 O(1+2+...+n)/n = O(n)。
  如果我们只是为了在索引为 k 的地方插入元素 a，有一个更省时的处理方式，就是把索引为 k 的元素搬到数组的最后，把 a 插入到位置 k，这其实就是快排的思想。

• 删除操作
  其实删除操作和插入操作的分析过程是一样的，时间复杂度为 O(n)。
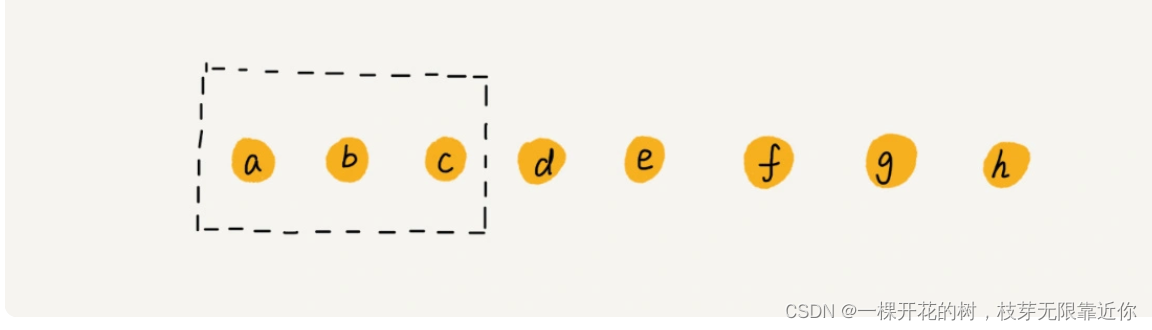
  如果我们要执行一系列的删除操作，例如要依次删除下面的 a、b、c，那么删除 a 的时候，b和c的搬运是不是就是浪费的？所以在删除操作中，我们可以先记录下打算删除哪个元素，并不真正的删除，等待一段时间后，再检查一下要删除的元素都有谁，批量进行删除。这就是 JVM 的垃圾回收的思想。好吧，本前端不会(傲娇.jpg)。
  
  回到前面的问题：为什么数组都是从 0 开始编号呢？
  回顾一下寻址公式：

a[i]_address = base_address + i * data_type_size

数组的索引记录的其实是相对于 base_address 的偏移量，第一个元素就是在 base_address 的位置，如果数组从 1 开始编号，那么根据寻址公式随机访问元素的时候，都要进行 i-1 的操作，浪费一次计算，所以从 0 开始可以有效的提高随机访问数组元素的效率。当然最开始的 c 语言可能是出于这个目的，后来的编程语言可能是为了和 c 语言保持统一，干脆都从 0 开始编号。