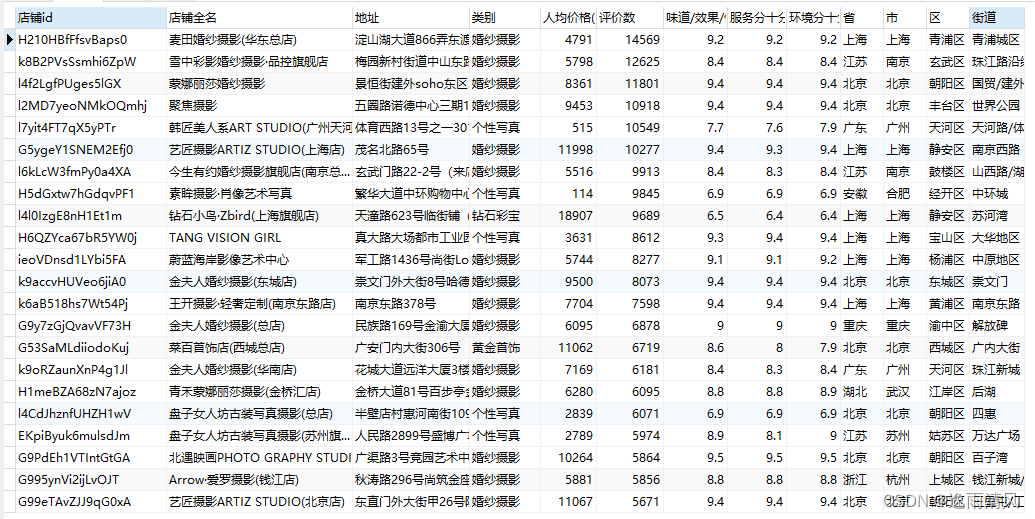
微♥关注“电击小子程高兴的MATLAB小屋”获得资料

一，理论基础

生物学家研究发现，蚂蚁在寻找食物时，会在其经过的路径上释放一种信息素，并能够感知其他蚂蚁释放的信息素。信息素浓度的大小表示路径的远近，浓度越高，表明对应的路径距离越短。通常，蚂蚁会以较大的概率优先选择信息素浓度较高的路径，并释放一定量的信息素，这样就形成一个正反馈。最终，蚂蚁能够找到一条从巢穴到食物源的最佳路径，即最短距离。同时，生物学家还发现，路径上的信息素浓度会随着时间的推移而逐渐衰减。

将蚁群算法(ant colony algorithm,ACA)应用于解决优化问题的基本思路为：用蚂蚁的行走路径表示待优化问题的可行解，整个蚂蚁群体的所有路径构成待优化问题的解空间。路径较短的蚂蚁释放的信息素量较多，随着时间的推移，较短的路径上累积的信息素浓度逐渐增高，选择该路径的蚂蚁数量也越来越多。最终，整个蚂蚁会在正反馈的作用下集中到最佳的路径上，此时对应的便是待优化问题的最优解。

二，蚁群算法解决TSP问题的基本步骤

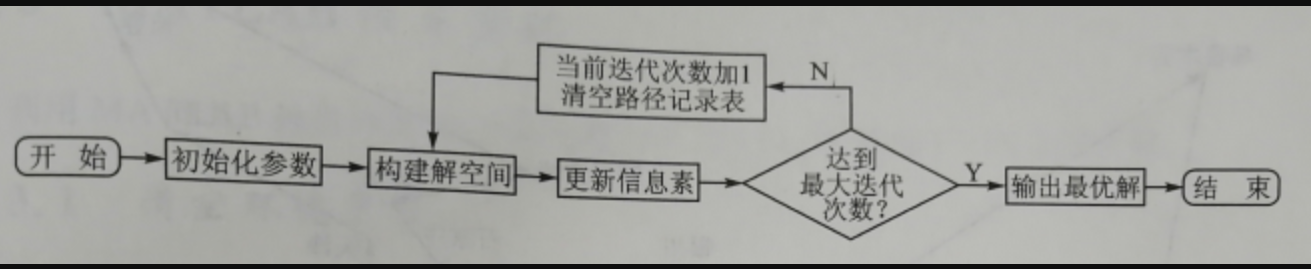
1.初始化参数在计算之初，需要对相关的参数进行初始化，如蚁群规模(蚂蚁数量)m、信息素重要程度因子a、启发函数重要程度因子β、信息素挥发因子p、信息素释放总量Q、最大迭代次数itermax、迭代次数初值iter = 1。

2.构建解空间

将各个蚂蚁随机地置于不同的出发地，对每个蚂蚁k(k = 1,2,…,m)，按照转移概率公式计算其下一个待访问的城市，直到所有蚂蚁访问完所有的城市。

3.更新信息素计算各个蚂蚁经过的路径长度L(k = 1,2.., m)，记录当前迭代次数中的最优解(最短路径)。同时，根据信息素更新公式和ant cycle system模型对名个城市连接路径上的信息素浓度进行更新。

4.判断是否终止

若iter < itermax，则令iter = iter +1，清空蚂蚁经过路径的记录表，并返回步骤2;否则，终止计算，输出最优解。

三，MATLAB程序实现

%% I. 清空环境变量
clear all
clc


%% II. 导入数据
load citys_data.mat


%% III. 计算城市间相互距离
n = size(citys, 1);   % 城市的个数
D = zeros(n, n);
for i = 1:n
    for j = 1:n
        if i ~= j
            D(i, j) = sqrt(sum((citys(i, :)-citys(j, :)).^2));
        else
            D(i, j) = 1e-4;
        end
    end
end


%% IV. 初始化参数
m = 50;                             % 蚂蚁数量
alpha = 1;                          % 信息素重要程度因子
beta = 5;                           % 启发函数重要程度因子
rho = 0.1;                          % 信息素挥发因子
Q = 1;                              % 常系数
Eta = 1./D;                         % 启发函数
Tau = ones(n, n);                   % 信息素矩阵
Table = zeros(m, n);                % 路径记录表
iter = 1;                           % 迭代次数初值
iter_max = 200;                     % 最大迭代次数
Route_best = zeros(iter_max, n);    % 各代最佳路径
Length_best = zeros(iter_max, 1);   % 各代最佳路径长度
Length_ave = zeros(iter_max, 1);    % 各代路径的平均长度

四，结果显示

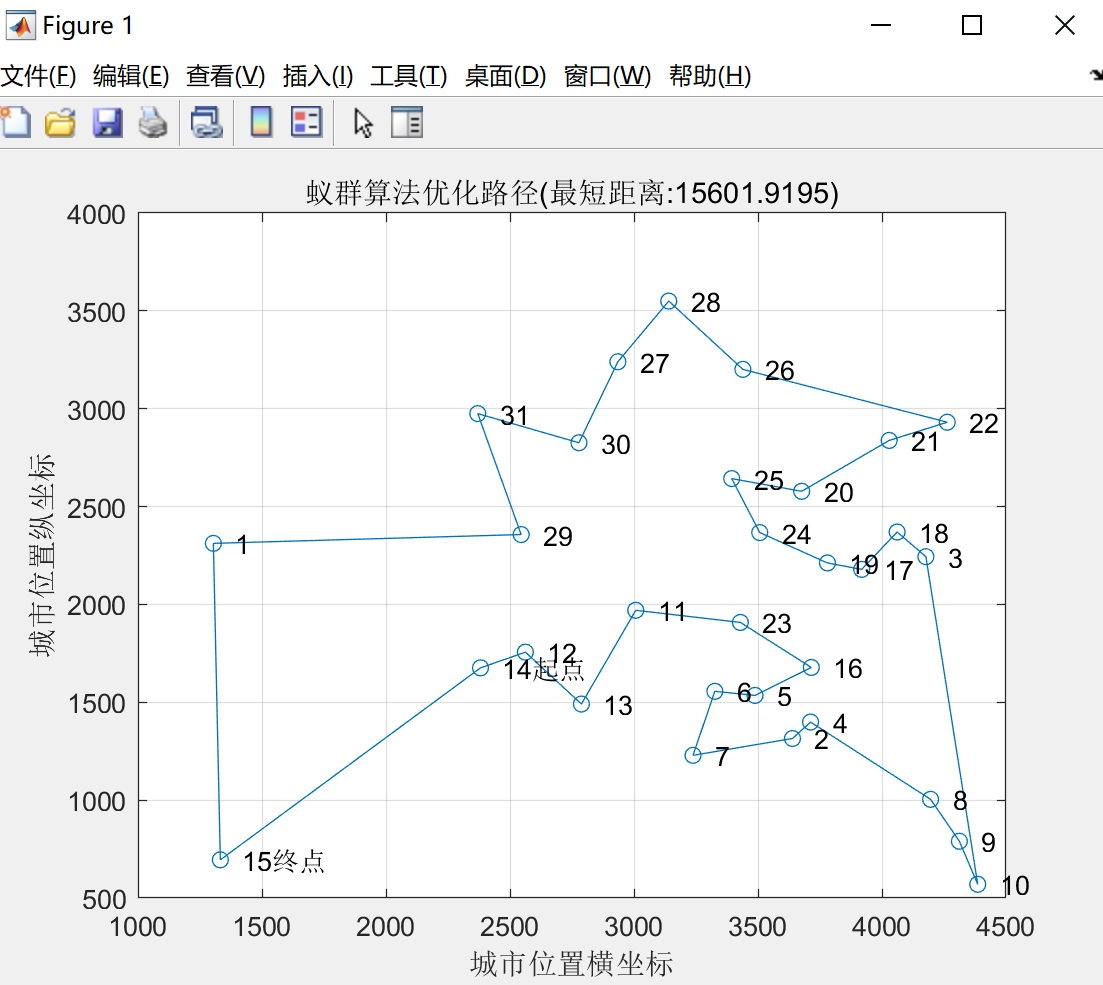
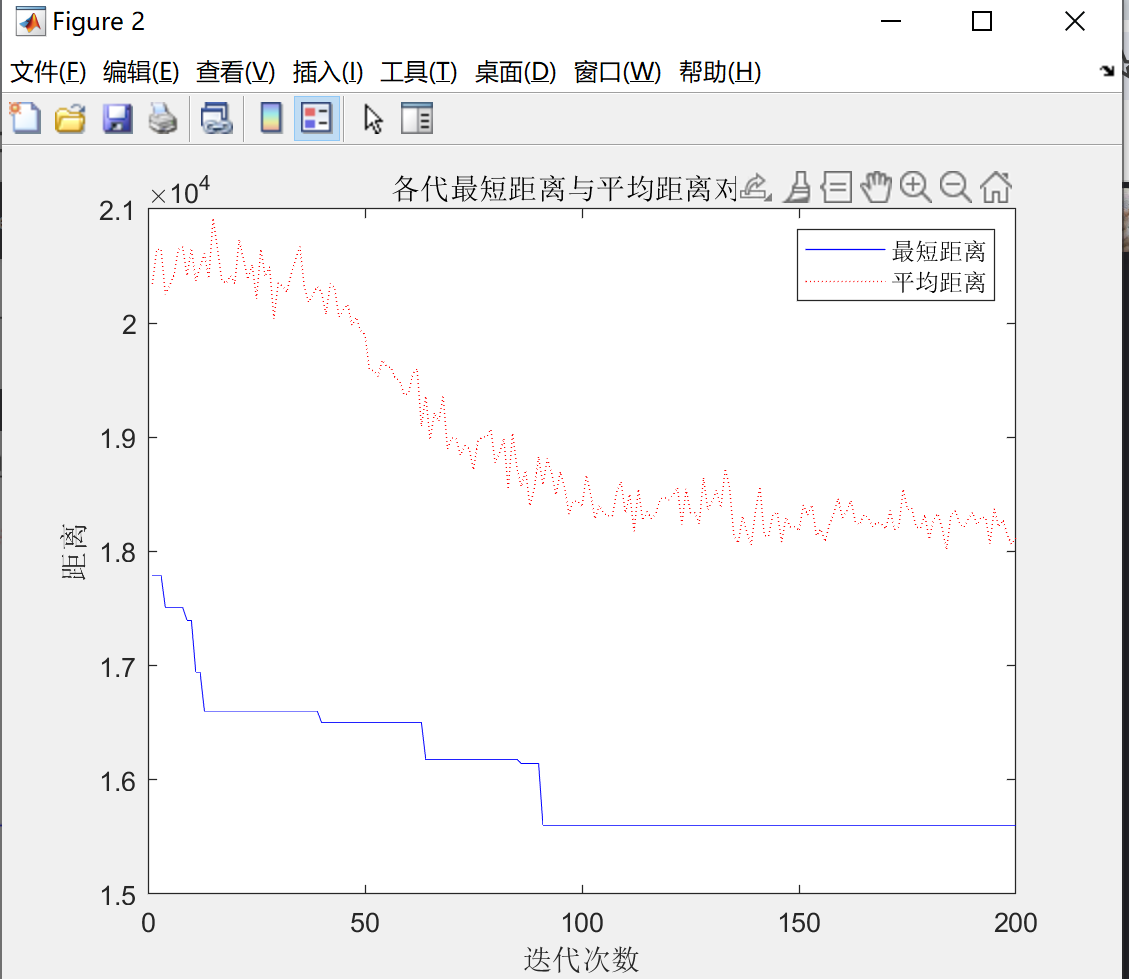
Command window中的运行结果：

最短距离15601.9195
最短路径30  27  28  26  22  21  20  25   24   19   17   18   3   10   9  8   4  2  7  6  5  16  23  11  13  12  14  15  1  29  31   30