$Autoformer$

摘要

​ 我们设计了$Autoformer$作为一种新型分解架构，带有自相关机制。我们打破了序列分解的预处理惯例，并将其革新为深度模型的基本内部模块。这种设计使$Autoformer$具备了对复杂时间序列的渐进分解能力。进一步地，受随机过程理论的启发，我们基于序列周期性设计了自相关机制，它在子序列级别进行依赖关系的发现和表示聚合。在效率和准确性方面，自相关机制都优于自注意力机制。

1.简介

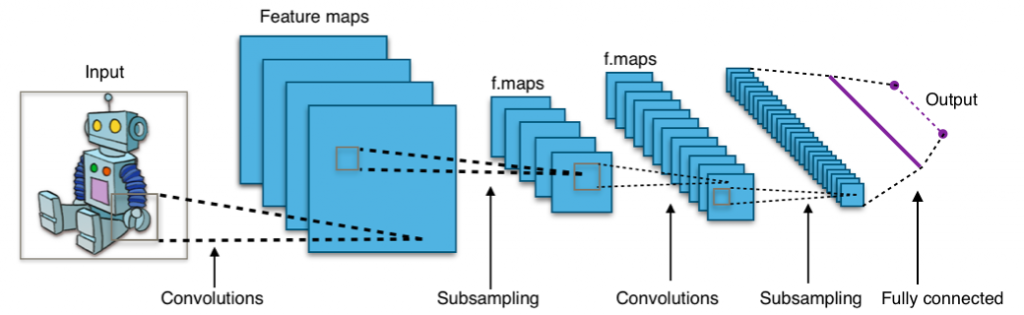
​ 最近的深度预测模型已经取得了很大的进展，特别是基于变压器的模型。得益于自关注机制，变压器在对序列数据的长期依赖关系建模方面具有很大的优势，这使得更强大的大模型成为可能。我们尝试利用序列的周期性来更新自关注中的点向连接。观察到，周期之间处于相同相位位置的子序列往往呈现相似的时间过程。因此，尝试基于序列周期性导出的过程相似性构建一个序列级连接。

​ 提出了一个原始的自耦器来代替变压器进行长期时间序列预测。自耦器仍然沿用残差和编解码器结构，但将变压器改造为分解预测结构。通过嵌入我们提出的分解块作为内部算子，自耦器器可以逐步从预测的隐藏变量中分离出长期趋势信息。这种设计允许我们的模型在预测过程中交替分解和细化中间结果。受随机过程理论的启发，自耦器引入了自相关机制来代替自关注，该机制基于序列的周期性发现子序列的相似性，并从底层周期中聚合相似的子序列。这种序列智能机制为长度为$L$的序列实现了$O(LlogL)$复杂度，并通过将逐点表示聚合扩展到子序列级别来打破信息利用瓶颈。自耦器在六个基准上达到了最先进的精度。贡献总结如下:

• 为了解决长期未来复杂的时间模式，我们提出了自耦器作为一个分解架构，并设计了内部分解块，以赋予深度预测模型具有内在的渐进分解能力。
• 我们提出了一种自相关机制，在序列级别上具有依赖性发现和信息聚合。我们的机制超越了以前的自关注家族，可以同时有利于计算效率和信息利用率。
• 在六个基准的长期设定下，自耦器实现了38%的相对改进，涵盖了五个实际应用:能源、交通、经济、天气和疾病。

2.相关工作

• 提出的自相关机制基于时间序列的固有周期性，可以提供序列明智的连接。
• 自耦器利用分解作为深度模型的内部块，可以在整个预测过程中逐步分解隐藏序列，包括过去的序列和预测的中间结果。

3.Autoformer

Autoformer架构：编码器通过序列分解模块（蓝色模块）消除长期趋势周期部分，并专注于季节性模式的建模。解码器逐步累积从隐藏变量中提取的趋势部分。编码器中的过去季节性信息被编码器-解码器自相关（解码器中央的绿色模块）所利用。

将$Transformer$​​改造为一个深度分解架构，包括内部的系列分解块、自相关机制以及相应的编码器和解码器。

序列分解模块:

​ 该模块的目的是将输入的时间序列分解为趋势周期部分和季节性部分，以便更好地进行长期预测。由于未来是未知的，因此该模块通过对预测的中间隐藏变量进行处理来提取长期稳定的趋势。具体方法是使用移动平均法，通过填充操作保持序列长度不变。最终，该模块输出分解后的季节性部分和趋势周期部分。

​ 采用移动平均法来平滑周期性波动，并突出长期趋势。对于长度为$L$的输入序列$X\in {\mathbb{R}}^{L\times d}$，其过程如下：
$$\begin{gathered} X_t=\text{AvgPool}(\text{Padding}(X)) \\ {X}_s=X-X_t \\ 方程一 \end{gathered}$$

​ 其中，$X_s$和$X_t\in {\mathbb{R}}^{L\times d}$分别表示季节性和提取的趋势周期部分。我们采用带有填充操作的$AvgPool(\cdot )$进行移动平均，以保持序列长度不变。我们用$Xs,Xt=SeriesDecomp(X)$​​​来总结上述方程，这是一个模型内部模块。

模型输入

​ 编码器的输入是过去$I$个时间步的$Xen\in R^{I\times d}$。作为一个分解架构，$Autoformer$解码器的输入包含两部分：季节性部分$X_{des}\in R^{(I/2+O)\times d}$和趋势周期部分$X_{det}\in R^{(I/2+O)\times d}$，这些部分需要被细化。每个初始化包含两部分：一部分是从编码器输入$X_{en}$的后半部分（长度为$I/2$）分解得到的组件以提供近期信息，另一部分是长度为$O$的占位符，用标量填充。具体数学公式如下：
$$\begin{array}{rl}\text{Xens},\text{Xent}& =\text{SeriesDecomp}({\text{Xen}}_{\frac{I}{2}:I})\\ \text{Xdes}& =\text{Concat}(\text{Xens},{\text{X}}_0)\\ \text{Xdet}& =\text{Concat}(\text{Xent},\text{XMean})\end{array}方程二$$

​ 其中，$X_{ens},X_{ent}\in R^{I/2\times d}$分别表示$X_{en}$的季节性和趋势周期部分，而$X_0,X_{Mean}\in R^{O\times d}$分别表示用零填充的占位符和$X_{en}$​的均值。

编码器

​ 编码器专注于季节性部分的建模。编码器的输出包含过去的季节性信息，并将作为交叉信息来帮助解码器细化预测结果。假设我们有$N$个编码器层。第$l$个编码器层的整体方程可以总结为$X_l^{\text{en}}=\text{Encoder}(X_{l-1}^{\text{en}})$。具体细节如下：
$$\begin{gathered} S_{en}^{l,1},\underline{}=SeriesDecomp(Auto-Correlation(X_{en}^{l-1})+X_{en}^{l-1}) \\ {S}_{en}^{l,2},\underline{}=SeriesDecomp(FeedForward(S_{en}^{l,1})+S_{en}^{l,1})方程三 \end{gathered}$$

​ 其中，${}^{\prime }\underline{}{}^{\prime }$表示被消除的趋势部分。$X_{en}^l$是第$l$个编码器层的输出，$X_{en}^0$是$X_{en}$的嵌入表示。 S e n l , i ， i ∈ { 1 , 2 } S_{en}^{l,i}，i∈\{1,2\} Senl,i​，i∈{1,2}，分别表示第$l$层中第$i$个序列分解块之后的季节性组件。我们将在下一节中详细描述$Auto-Correlation(\cdot )$​，它可以无缝地替代自注意力机制。

解码器

​ 解码器包含两个部分：用于趋势周期分量的累积结构，以及用于季节组分的堆叠自相关机制。每个解码器层都包含内部自相关和编码器-解码器自相关，这可以分别细化预测并利用过去的季节信息。模型在解码过程中从中间的隐藏变量中提取潜在趋势，允许$Autoformer$逐步细化趋势预测，并消除在自相关中发现基于周期的依赖关系时的干扰信息。假设有$M$个解码器层。利用来自编码器的潜变量$X_{en}^N$，第$l$个解码器层的方程可以总结为$X_{de}^l=Decoder(X_{de}^{l-1},X_{en}^N)$。解码器可以形式化如下：
$$\begin{array}{rl}{S}_{l,1}^{de},T_{l,1}^{de}& =\text{SeriesDecomp (Auto-Correlation}(X_{l-1}^{de})+X_{l-1}^{de})\\ S_{l,2}^{de},T_{l,2}^{de}& =\text{SeriesDecomp (Auto-Correlation}(S_{l,1}^{de},X_N^{en})+S_{l,1}^{de})\\ S_{l,3}^{de},T_{l,3}^{de}& =\text{SeriesDecomp (FeedForward}(S_{l,2}^{de})+S_{l,2}^{de})\\ T_l^{de}& =T_{l-1}^{de}+W_{l,1}\ast T_{l,1}^{de}+W_{l,2}\ast T_{l,2}^{de}+W_{l,3}\ast T_{l,3}^{de}\end{array}方程四$$
​ 其中， X d e l = S d e l , 3 , l ∈ { 1 , . . . , M } X_{de}^l=S_{de}^{l,3},l\in\{1,...,M\} Xdel​=Sdel,3​,l∈{1,...,M}表示第$l$层解码器的输出。$X_0^{de}$ 是从 $X_{des}$ 中嵌入的，用于深度变换，而 $T_0^{de}=X_{det}$ 用于累积。$S_{l,i}^{de}$ 和 $T_{l,i}^{de}$，其中 i ∈ { 1 , 2 , 3 } i ∈ \{1, 2, 3\} i∈{1,2,3}，分别表示在第 $l$ 层中经过第 $i$ 个序列分解块后的季节组分和趋势-周期组分。$W_{l,i}$，其中 i ∈ { 1 , 2 , 3 } i ∈ \{1, 2, 3\} i∈{1,2,3}，表示第$i$ 个提取的趋势 $T_{l,i}^{de}$ 的投影器。

​ 最终的预测是这两个细化后的分解组分的和，即 $W_S\ast X_M^{de}+T_M^{de}$，其中$W_S$ 是将深度变换后的季节组分 $X_M^{de}$ 投影到目标维度的投影器。

自相关机制

图2：自相关（左）和时间延迟聚合（右）。我们利用快速傅里叶变换（Fast Fourier Transform）来计算自相关函数R(τ)，该函数反映了时间延迟的相似性。然后，基于选定的延迟τ，将相似的子过程滚动到相同的索引位置，并通过R(τ)进行聚合

​ 提出了具有序列间连接的自相关机制，以扩大信息利用率。自相关机制通过计算序列的自相关来发现基于周期的依赖关系，并通过时间延迟聚合来聚合相似的子序列。

基于周期的依赖关系，观察到在周期中的相同相位位置自然提供了相似的子过程。受随机过程理论的启发，对于一个真实的离散时间过程 { X t } \{X_t\} {Xt​}，我们可以通过以下方程得到自相关$R_{XX}(\tau )$：
$$\begin{gathered} R_{XX}(\tau )=\underset{L\to \infty }{\lim }\frac{1}{L}\sum _{t=1}^L{X}_t{X}_{t-\tau } \\ 方程五 \end{gathered}$$

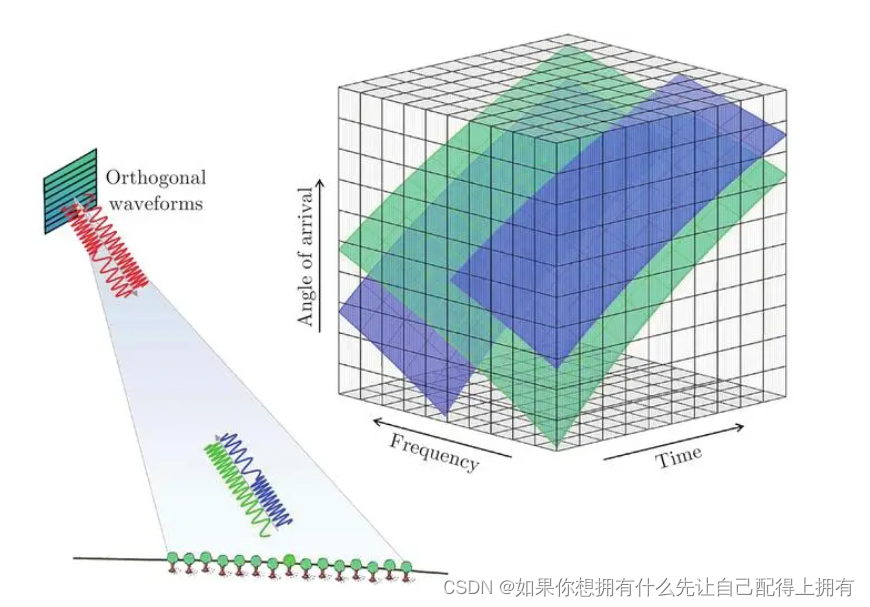
$R_{XX}(\tau )$反映了 { X t } \{X_t\} {Xt​}与其延迟$\tau$的序列 { X t − τ } \{X_{t−τ}\} {Xt−τ​}之间的时间延迟相似性。如图所示，我们使用自相关$R(\tau )$作为估计周期长度τ的非标准化置信度。然后，我们选择最可能的$k$个周期长度${\tau }_1,\dots ,{\tau }_k$。基于上述估计的周期，可以推导出基于周期的依赖关系，并可以通过相应的自相关进行加权。

时间延迟聚合 基于周期的依赖关系连接了估计周期内的子序列。因此，我们提出了时间延迟聚合模块，该模块可以根据选定的时间延迟${\tau }_1,\dots ,{\tau }_k$滚动序列。这种操作可以将处于估计周期相同相位位置的相似子序列对齐，这与自注意力家族中的逐点点积聚合不同。最后，我们通过$softmax$归一化的置信度聚合子序列。对于单头情况和长度为$L$的时间序列$X$，经过投影器后，我们得到查询$Q$、键$K$和值$V$。因此，它可以无缝地替代自注意力。自相关机制如下：
τ 1 , … , τ k = arg Top k { R Q , K ( τ ) } R ^ Q , K ( τ 1 ) , … , R ^ Q , K ( τ k ) = SoftMax ( R Q , K ( τ 1 ) , … , R Q , K ( τ k ) ) Auto-Correlation ( Q , K , V ) = ∑ i = 1 k Roll ( V , τ i ) ⋅ R ^ Q , K ( τ i ) 方程六 \tau_1, \ldots, \tau_k = \text{arg Top}_k \left\{ R_{Q, K}(\tau) \right\} \\ \widehat{R}_{Q, K}(\tau_1), \ldots, \widehat{R}_{Q, K}(\tau_k) = \text{SoftMax} \left( R_{Q, K}(\tau_1), \ldots, R_{Q, K}(\tau_k) \right) \\ \text{Auto-Correlation}(Q, K, V) = \sum_{i=1}^{k} \text{Roll}(V, \tau_i) \cdot \widehat{R}_{Q, K}(\tau_i)\\方程六 τ1​,…,τk​=arg Topk​{RQ,K​(τ)}R Q,K​(τ1​),…,R Q,K​(τk​)=SoftMax(RQ,K​(τ1​),…,RQ,K​(τk​))Auto-Correlation(Q,K,V)=i=1∑k​Roll(V,τi​)⋅R Q,K​(τi​)方程六

​ 其中$argTopk(\cdot )$是获取$Topk$个自相关值的参数，并令$k=\lfloor c×logL \rfloor $，$c$是一个超参数。$R_{Q,K}$是序列$Q$和$K$之间的自相关。$Roll(X,τ)$表示对\ast X\ast 进行时间延迟$τ$的操作，其中超出第一个位置的元素将被重新引入到最后的位置。对于编码器-解码器自相关，$K$、$V$来自编码器$X_{en}^N$并会被调整为长度$O$，而$Q$来自解码器的前一个块。对于$Autoformer$中使用的多头版本，具有$d_{model}$个通道和$h$个头的隐藏变量，第$i$个头的查询、键和值是$Q_i,K_i,V_i\in \mathbb{R}^{L\times \frac{d_{model}}{h}},i\in{1,…,h}$，。其过程如下：
$$\begin{gathered} \text{MultiHead}(Q,K,V)=W_{\text{output}}\times \text{Concat}({\text{head}}_1,\dots ,{\text{head}}_h) \\ \text{where }{\text{head}}_i=\text{Auto-Correlation}(Q_i,K_i,V_i) \\ 方程七 \end{gathered}$$
高效计算：对于基于周期的依赖关系，这些依赖关系指向底层周期中相同相位位置的子过程，并且本质上是稀疏的。在这里，我们选择最可能的延迟来避免选择相反的相位。由于我们聚合了$O(logL)$个长度为$L$的序列，因此方程$6$和$7$的复杂度为$O(LlogL)$。对于自相关计算（方程$5$），给定时间序列 { X t } ， R X X ( τ ) \{X_t\}，R_{X X} (τ) {Xt​}，RXX​(τ)可以通过基于维纳-辛钦定理的快速傅里叶变换（$FFT$）来计算：
$$\begin{array}{rl}{S}_{XX}(f)& =F(X_t)F^{\ast }(X_t)={\int }_{-\infty }^{\infty }{X}_t{e}^{-i2\pi tf}dt\cdot {\overline{{\int }_{-\infty }^{\infty }{X}_t{e}^{-i2\pi tf}dt}}^{}\\ R_{XX}(\tau )& =F^{-1}(S_{XX}(f))={\int }_{-\infty }^{\infty }{S}_{XX}(f)e^{i2\pi f\tau },df\end{array}方程八$$

其中 τ ∈ { 1 , . . . , L } τ ∈ \{1, ..., L\} τ∈{1,...,L}，$F$表示$FFT$，$F^{-1}$是其逆变换。$\ast$表示共轭操作，$S_{XX}(f)$是频域中的。请注意，通过$FFT$可以一次性计算 { 1 , . . . , L } \{1, ..., L\} {1,...,L}中所有延迟的序列自相关。因此，自相关计算达到了$O(LlogL)$​的复杂度。

自相关与自注意族

图3：自相关与自注意力家族的比较。全注意力（a）适用于所有时间点之间的完全连接。稀疏注意力（b）基于提出的相似度指标选择点。对数稀疏注意力（c）选择点遵循指数增加的间隔。自相关（d）关注底层周期中子序列之间的连接。

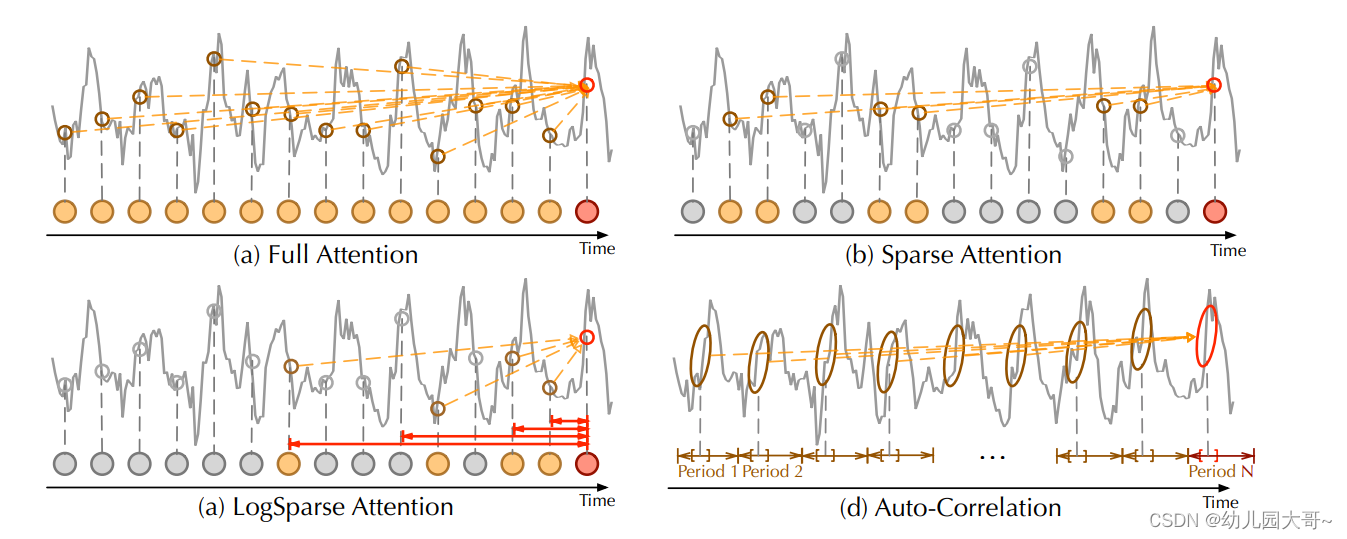
​ 与逐点自注意力族不同，自相关展示了序列之间的连接（如图所示）。具体来说，对于时间依赖性,我们基于周期性来查找子序列之间的依赖关系。相比之下，自注意力族仅计算分散点之间的关系。尽管一些自注意力机制考虑了局部信息，但它们仅利用这些信息来帮助发现逐点依赖关系。对于信息聚合，我们采用时间延迟块来聚合来自底层周期中的相似子序列。相反，自注意力通过点积来聚合选定的点。得益于固有的稀疏性和子序列级别的表示聚合，自相关可以同时提高计算效率和信息利用率。

4.实验