491. 非递减子序列

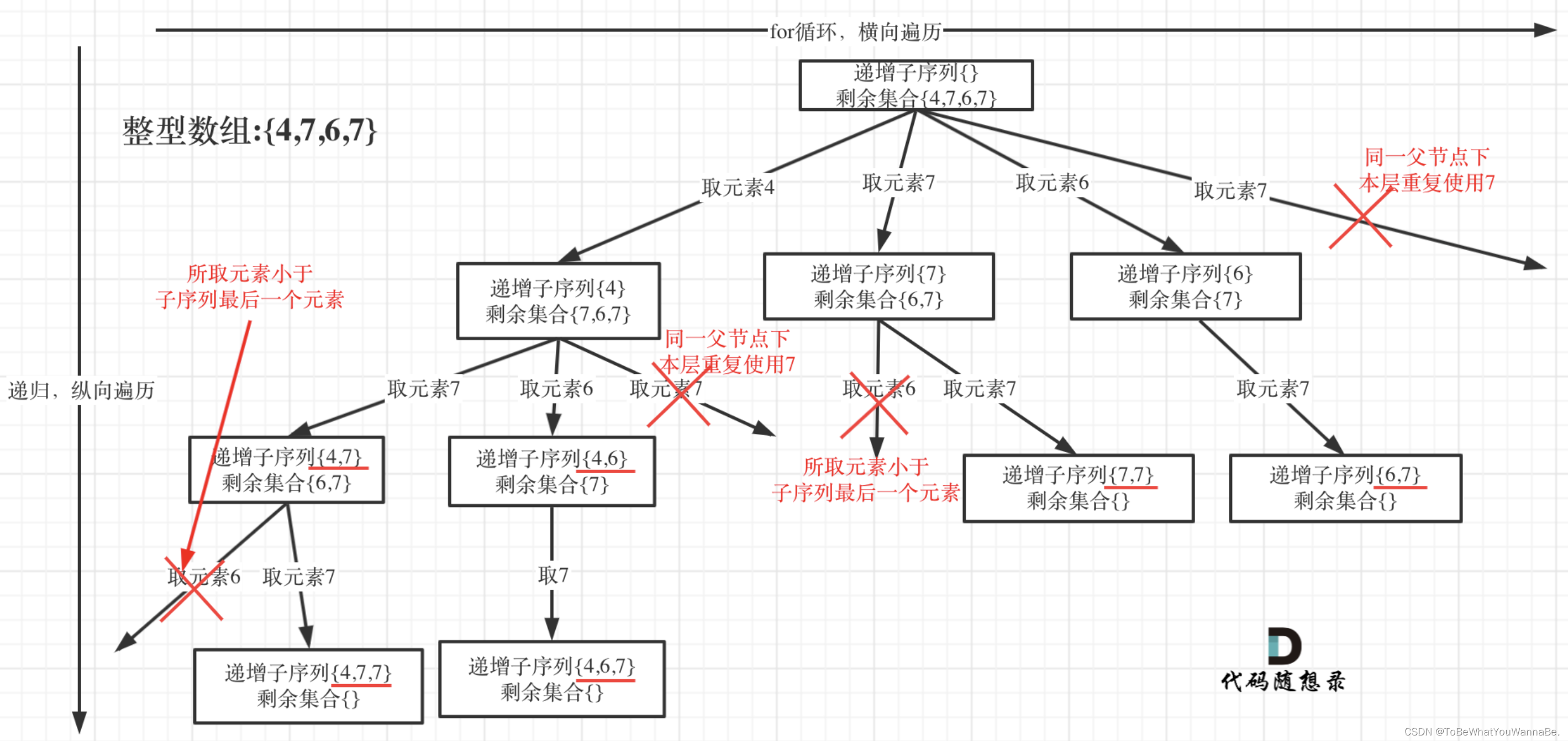
给你一个整数数组 nums ，找出并返回所有该数组中不同的递增子序列，递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。

数组中可能含有重复元素，如出现两个整数相等，也可以视作递增序列的一种特殊情况。

示例 1：
输入：nums = [4,6,7,7]
输出：[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]
示例 2：
输入：nums = [4,4,3,2,1]
输出：[[4,4]]

class Solution {
    private List<Integer> path = new ArrayList<>();
    private List<List<Integer>> res = new ArrayList<>();
    public List<List<Integer>> findSubsequences(int[] nums) {
        backtracking(nums,0);
        return res;
    }

    private void backtracking (int[] nums, int start) {
        if (path.size() > 1) {
            res.add(new ArrayList<>(path));
        }

        int[] used = new int[201];
        for (int i = start; i < nums.length; i++) {
            if (!path.isEmpty() && nums[i] < path.get(path.size() - 1) ||
                    (used[nums[i] + 100] == 1)) continue;
            used[nums[i] + 100] = 1;
            path.add(nums[i]);
            backtracking(nums, i + 1);
            path.remove(path.size() - 1);
        }
    }
}

这段代码定义了一个名为Solution的类，该类包含方法用于寻找给定整数数组nums中所有递增的非空子序列。递增子序列是指数组中数字按顺序排列（每个数字可以重复）的子集。以下是代码的详细解析：

类成员变量

• path: 一个List<Integer>类型的变量，用于存储当前递归路径上的数字，即当前正在构建的递增子序列。
• res: 另一个List<List<Integer>>类型的变量，用于存储所有找到的递增子序列。

方法 findSubsequences

• 功能: 接收一个整型数组nums作为输入，返回该数组的所有递增非空子序列。
• 实现: 首先调用backtracking方法启动回溯过程，并返回最终结果列表res。

方法 backtracking

• 输入参数:
  • nums: 整型数组，全局输入数据。
  • start: 整型变量，表示当前回溯搜索的起始位置，避免重复使用已经确定不在子序列中的元素。
• 功能: 通过回溯算法递归地构建所有递增子序列。

回溯核心逻辑

1. 剪枝: 如果当前路径path的大小超过1（意味着至少有两个元素），说明找到了一个有效的递增子序列，将其添加到结果列表res中。

2. 避免重复: 引入一个整型数组used来标记当前层递归中nums[i]是否已经被使用过，以避免生成重复子序列。数组大小为201，是因为整数范围为-100到100，通过加100映射到数组索引中，这样可以使用正数索引，简化判断和访问逻辑。

3. 遍历与选择: 从start位置开始遍历nums数组，对于每个元素，执行以下操作：

   • 如果当前路径非空且新元素小于路径尾部元素，或者当前元素在当前层已使用过（由used数组判断），则跳过此次循环继续下一个元素，这是为了保证子序列递增且不重复。
   • 标记当前元素在当前层已使用。
   • 将当前元素加入路径path。
   • 以当前位置的下一个元素为起点，进行下一层递归调用。
   • 回溯：从路径中移除最后一个元素，恢复到上一步状态，尝试下一个可能的选择。

最终，当回溯过程完成，所有递增子序列会被收集在res中，并由findSubsequences方法返回。

46. 全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

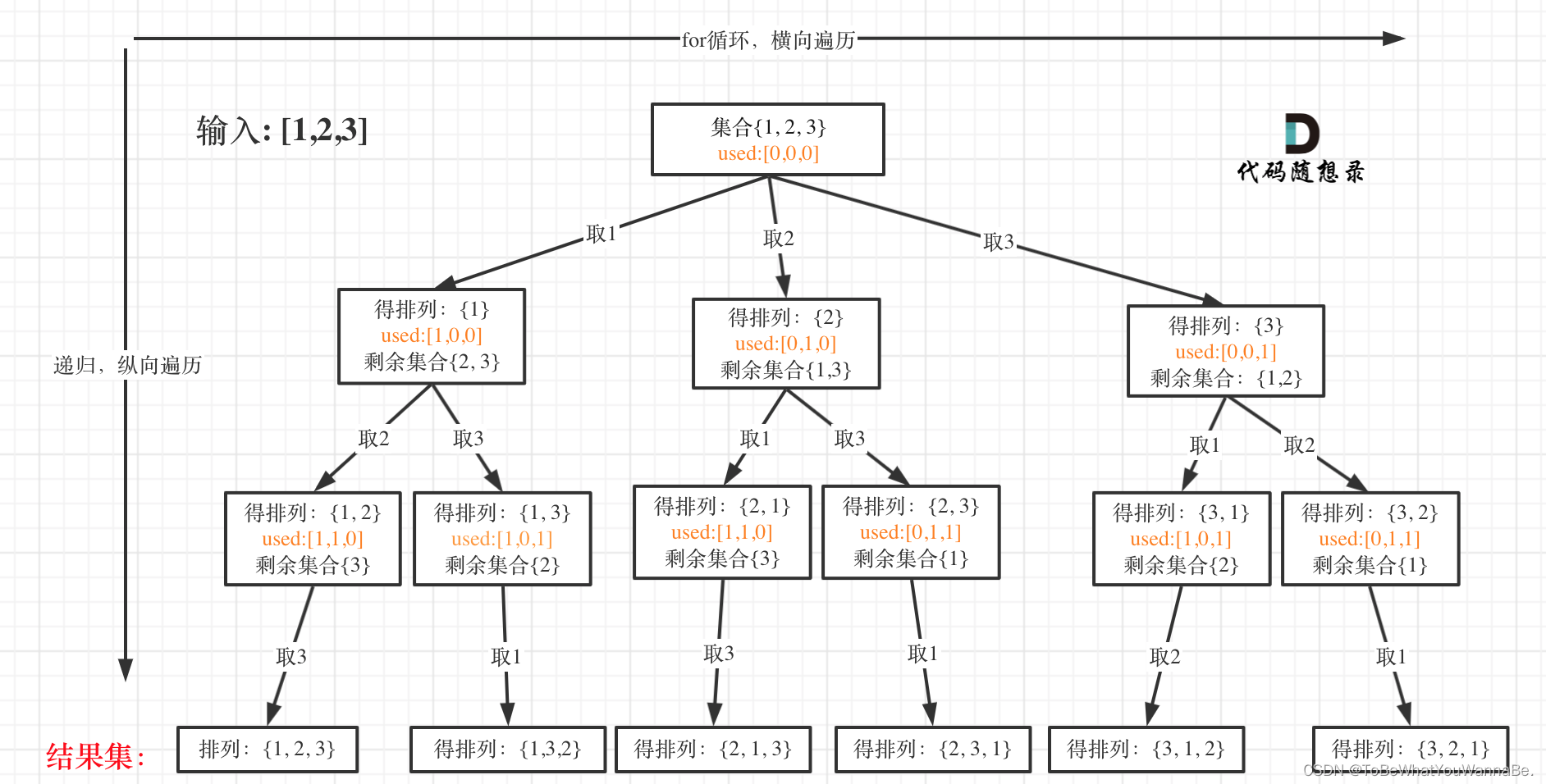
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]
示例 3：

输入：nums = [1]
输出：[[1]]

class Solution {

    List<List<Integer>> result = new ArrayList<>();// 存放符合条件结果的集合
    LinkedList<Integer> path = new LinkedList<>();// 用来存放符合条件结果
    boolean[] used;
    public List<List<Integer>> permute(int[] nums) {
        if (nums.length == 0){
            return result;
        }
        used = new boolean[nums.length];
        permuteHelper(nums);
        return result;
    }

    private void permuteHelper(int[] nums){
        if (path.size() == nums.length){
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < nums.length; i++){
            if (used[i]){
                continue;
            }
            used[i] = true;
            path.add(nums[i]);
            permuteHelper(nums);
            path.removeLast();
            used[i] = false;
        }
    }
}

这段代码定义了一个名为Solution的类，其中主要实现了获取一个整型数组所有可能的排列组合的功能。下面是详细的解析：

类成员变量

• result: 类型为List<List<Integer>>，用于存储所有满足条件的排列结果。
• path: 类型为LinkedList<Integer>，作为一个临时列表，用于在递归过程中暂存当前排列。
• used: 类型为boolean[]，标记数组中的元素在当前排列中是否已被使用过，避免重复选择。

方法 permute

• 功能: 接收一个整型数组nums作为输入，返回该数组所有可能的排列组合。
• 逻辑:
  • 首先检查输入数组是否为空，若为空直接返回空结果列表。
  • 初始化布尔数组used，长度与输入数组相同，用于记录每个元素的使用状态。
  • 调用辅助函数permuteHelper(nums)来进行实际的排列生成。

方法 permuteHelper

• 功能: 实现深度优先搜索(DFS)回溯算法来生成所有排列。
• 逻辑:
  • 当path的大小等于原数组长度时，说明已经生成了一个完整的排列，将其添加到结果列表result中，然后返回。
  • 对于数组nums中的每个元素，进行以下操作：
    • 若该元素已经在当前排列中使用过（used[i] == true），则跳过，避免重复。
    • 标记该元素为已使用(used[i] = true)，将它添加到path中。
    • 递归调用permuteHelper(nums)生成剩余元素的排列。
    • 在递归调用返回后（即处理完以当前元素为固定位置的所有情况），需要“撤销”选择：将used[i]重置为false，并将nums[i]从path中移除，回溯到上一层继续尝试其他元素。

综上所述，这个程序利用回溯算法深度优先遍历所有可能的排列组合情况，有效地解决了给定数组元素的全排列问题。