目录
- 一、背景介绍
- 二、思路&方案
- 三、过程
- 1.思维导图
- 2.文章中经典的句子理解
- 3.学习之后对于投资市场的理解
- 4.通过这篇文章结合我知道的东西我能想到什么?
- 四、总结
- 五、升华
一、背景介绍
信息的正交性,让我们对信息有足够的判断,可以避免上当。
二、思路&方案
- 1.思维导图
- 2.文章中经典的句子理解
- 3.学习之后对于投资市场的理解
- 4.通过这篇文章结合我知道的东西我能想到什么?
三、过程
1.思维导图
2.文章中经典的句子理解
- 2.1.当面对信息很多的时候,如何利用和组合信息,提高自己的决策水平?
- 2.2.信息并不具有守恒这个特点,比如你将一条信息告诉别人,你自己并不损失这条信息
- 2.3.和能量不同,相同的信息使用两次,不会产生两倍的效果
- 2.4.你使用同一条信息后,第二次使用它就没有用了,你使用一万次,结果还是一样
- 2.5.力的叠加方向要一致;信息的叠加正交的时候,效果最好
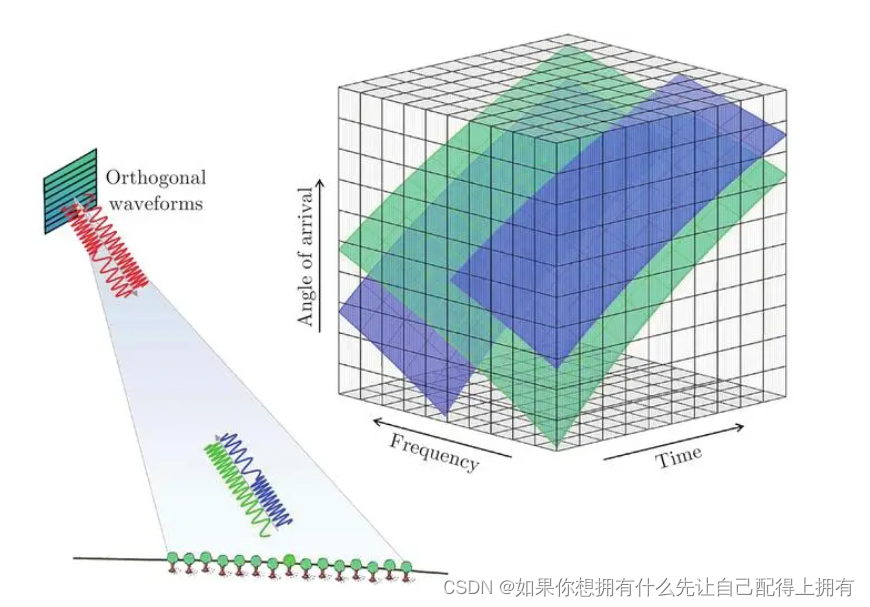
- 2.6.之前人们通过图像扫描得到的信息,和她从互联网上找到的信息,不仅属于不同的维度,而且是彼此近乎正交的
- 2.7.找到正交信息:不同的信息要来自不同的信息源
- 2.8.很多人容易上当的一个原因,就是他们不善于选用正交的信息进行交叉验证
- 2.9.避免反复使用相互嵌套或者相互包含的信息,第二个原则
- 2.10.看问题要刻意改变一下观察的角度,从几个不同的角度看
- 2.11.多种信息源中,如何选取几种最重要而且彼此尽可能正交的信息?两个方法:不断叠加,不断删除
3.学习之后对于投资市场的理解
一定要找到正交的信息,利用这些信息的时候才会更有效
4.通过这篇文章结合我知道的东西我能想到什么?
- 4.1.培养组合的意识和习惯,去遍历组合的所有可能
- 4.2.信息与能量的区别,以及他们的关系
四、总结
- 1.当面对无限的时候,就需要我们通过不同维度的交叉来应对
- 2.信息的正交方式,完全突破了人的直觉
五、升华
信息正交,这其实与我们每个人要两条腿走路,以及找另一半要门当户对是一个逻辑。
来自得到app中,吴军老师《信息论40讲》详读总结
![luogu-P10570 [JRKSJ R8] 网球](https://img-blog.csdnimg.cn/direct/57c6dc8bc83e4f9bbfce0a4d514df175.png)