【人工智能基础学习】Andrew Ng-机器学习基础笔记

news2025/1/16 17:31:20

⭐️我叫忆_恒心，一名喜欢书写博客的研究生👨‍🎓。
如果觉得本文能帮到您，麻烦点个赞👍呗！

近期会不断在专栏里进行更新讲解博客~~~
有什么问题的小伙伴欢迎留言提问欧，喜欢的小伙伴给个三连支持一下呗。👍⭐️❤️
📂Qt5.9专栏定期更新Qt的一些项目Demo
📂项目与比赛专栏定期更新比赛的一些心得，面试项目常被问到的知识点。
欢迎评论 💬点赞👍🏻 收藏 ⭐️加关注+
✍🏻文末可以进行资料和源码获取欧😄

摘要

深入探讨了机器学习的基础概念，尤其是监督学习和无监督学习。我们将重点介绍两种主要的机器学习方法——线性回归和梯度下降，帮助初学者理解这些基本算法及其应用。在具体讨论线性回归时，我们会详细讲解模型的表示、代价函数的计算及其直观理解。此外，我们还会深入探讨梯度下降算法，包括其直观解释和在实际问题中的应用。

1. 引言

1.1 欢迎:

在这篇博客中，我们将探讨机器学习中的主要问题和算法，帮助大家了解不同算法在各种应用场景中的具体使用。

1.2 机器学习是什么？

机器学习是指计算机通过经验（E）来提高其在任务（T）上的性能（P）。正如Tom Mitchell所说，“当一个程序在执行任务T时，如果它在经过经验E后，其表现按P标准衡量有所提升，那么这个程序就被认为是从经验E中学习到了。” 机器学习算法通常分为监督学习和无监督学习。

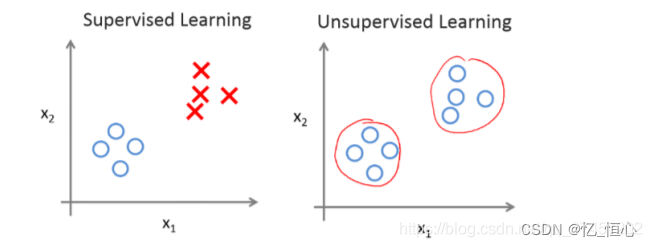
1.3 监督学习

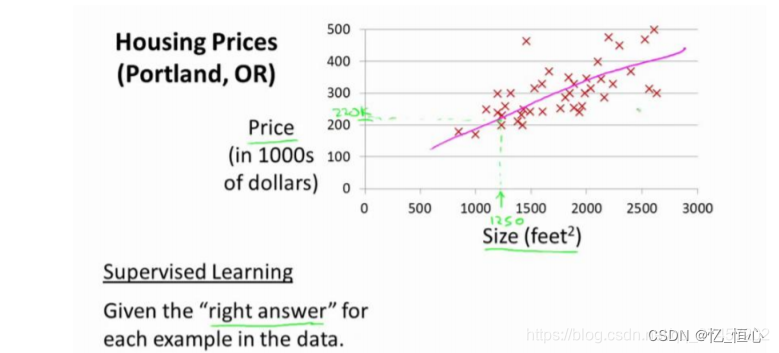
在这里插入图片描述

在监督学习中，我们提供给算法一个包含“正确答案”的数据集。两种常见的监督学习问题是回归问题和分类问题。

回归问题：例如，预测房价。我们有一系列房屋的历史数据，包括每个房屋的特征和实际售价。利用这些数据，算法可以预测新房屋的价格。
分类问题：例如，诊断肿瘤的良性或恶性。我们可以使用分类算法，根据已知的良性和恶性肿瘤数据，预测一个新肿瘤是良性还是恶性。

在处理特征非常多的情况下，我们可以使用支持向量机（SVM），这种算法通过巧妙的数学技巧，可以处理无数多个特征。

1.4 无监督学习

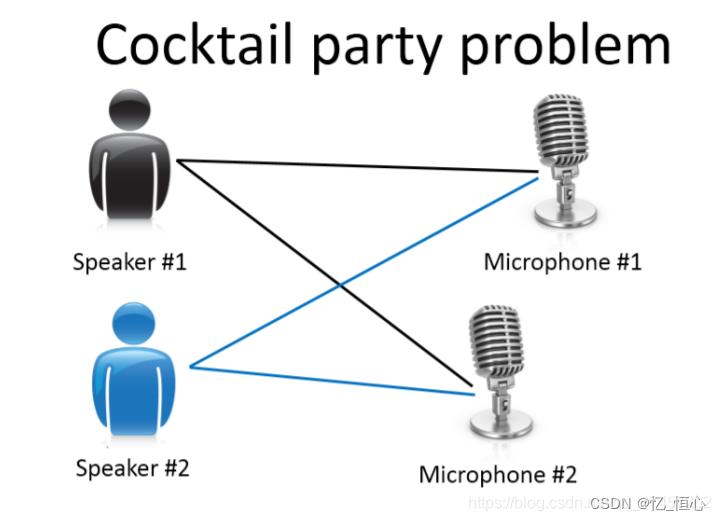
无监督学习与监督学习不同，它处理没有标签的数据。无监督学习算法会尝试发现数据中的模式和结构，例如将数据分成不同的组（聚类）。
在这里插入图片描述

聚类算法：例如，鸡尾酒会问题，通过聚类算法将不同的声音分开。

总结：

垃圾邮件过滤——监督学习
新闻事件分类——无监督学习
细分市场分析——无监督学习
糖尿病诊断——监督学习

在这里插入图片描述

2. 线性回归

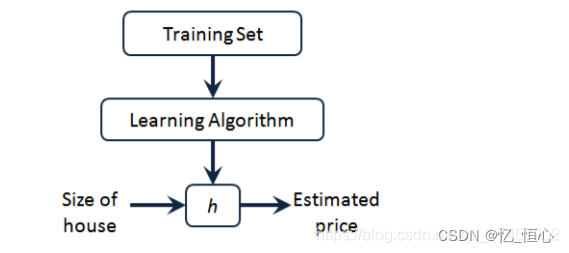
2.1 模型表示

在监督学习中，我们使用一个训练集来构建模型。以房价预测为例，我们可以使用线性回归来找到特征与房价之间的关系。
在这里插入图片描述

线性回归模型的表示形式通常是一个线性函数，其中只有一个特征变量时，我们称之为单变量线性回归。
在这里插入图片描述

2.2 代价函数

为了找到最佳的模型参数，我们需要最小化模型预测与实际数据之间的误差。代价函数用于量化这种误差：
在这里插入图片描述

$[ J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (h_{\theta}(x^{(i)}) - y{(i)})2 ]$

其中，( m ) 是训练样本的数量，( h_{\theta}(x^{(i)}) ) 是模型的预测值，( y^{(i)} ) 是实际值。

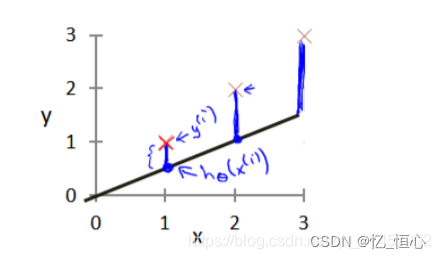
2.3 代价函数的直观理解

我们可以通过可视化代价函数的变化来理解其行为。例如，在只有一个参数的情况下，代价函数呈现为一个抛物线形状。通过找到代价函数的最低点，我们可以确定最优参数。
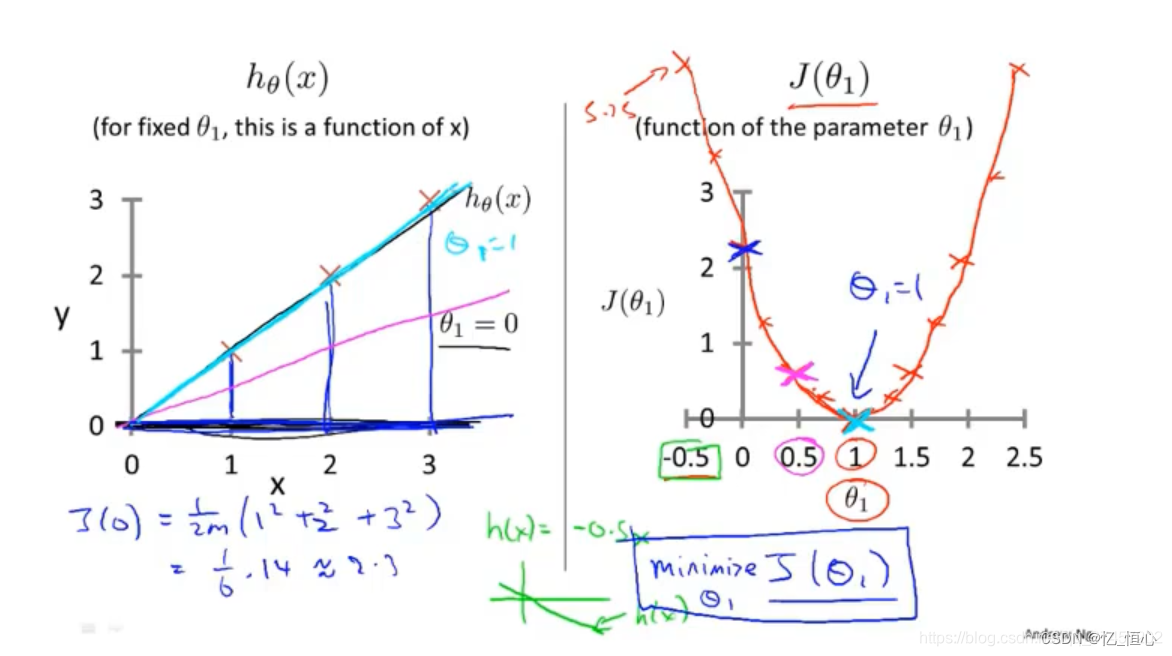
在这里插入图片描述

2.4 代价函数的等高线图

当我们考虑两个或更多参数时，代价函数的图像会变得复杂。在这种情况下，我们使用等高线图来表示代价函数的变化，从而帮助我们找到使代价函数最小化的参数。
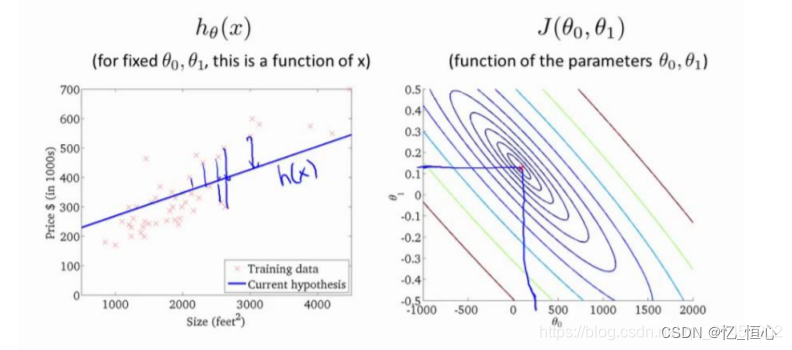
在这里插入图片描述

2.5 梯度下降

梯度下降是一种用于找到函数最小值的优化算法。在机器学习中，我们使用梯度下降来最小化代价函数，从而找到最佳的模型参数。
在这里插入图片描述

批量梯度下降：在每一步迭代中，利用所有的训练样本来更新模型参数：

\[
\theta_j := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^{m} (h_{\theta}(x^{(i)}) - y^{(i)}) x_j^{(i)}
\]

其中，( \alpha ) 是学习率，决定了每一步的移动大小。

Python实现代码示例：

def gradientDescent(X, y, theta, alpha, iters):
    temp = np.zeros(theta.shape)
    parameters = int(theta.shape[1])
    cost = np.zeros(iters)
    
    for i in range(iters):
        error = X @ theta.T - y
        for j in range(parameters):
            term = np.multiply(error, X[:, j])
            temp[0, j] = theta[0, j] - ((alpha / len(X)) * np.sum(term))
        theta = temp
        cost[i] = computeCost(X, y, theta)
    
    return theta, cost