一、测试
如果我们写出一下一些泛化的函数,①计算边长为r的正方形面积②半径为r的圆的面积③边长为r的六边形面积。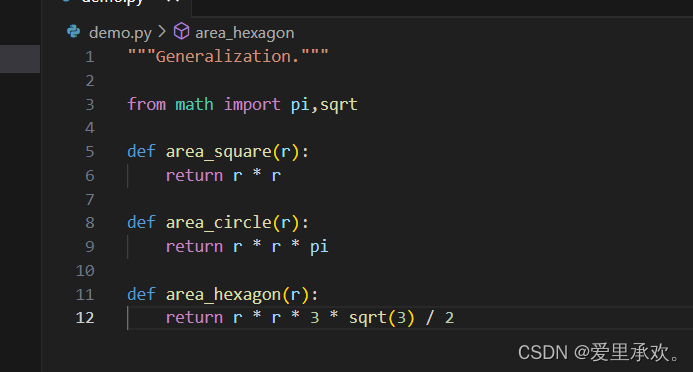
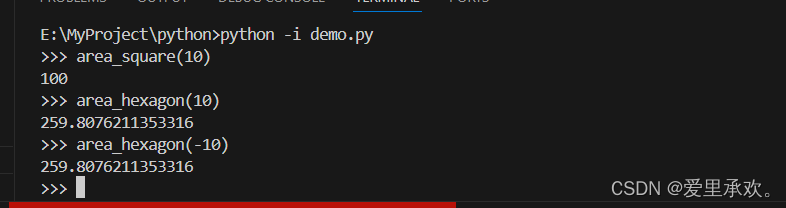
我们运行代码计算一下边长为10的六边形面积,可以看到它约等于260,但是我们计算一下边长为-10的六边形面积它也同样成功了,且值还一样,这很显然是不合理的。这时我们就需要"assert"来工作了。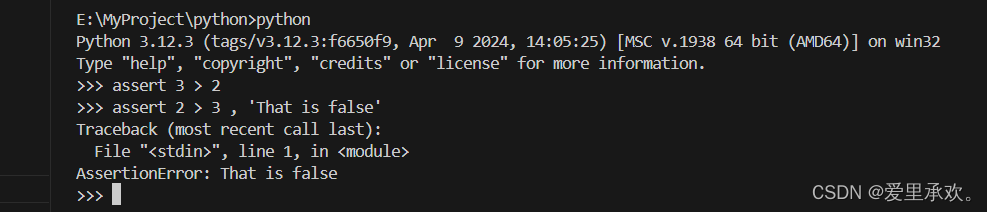

我们可以在上图位置加上一个断言,这样就要复制三份一样的代码,我们可以分析这三个例子的共同点来概括它们。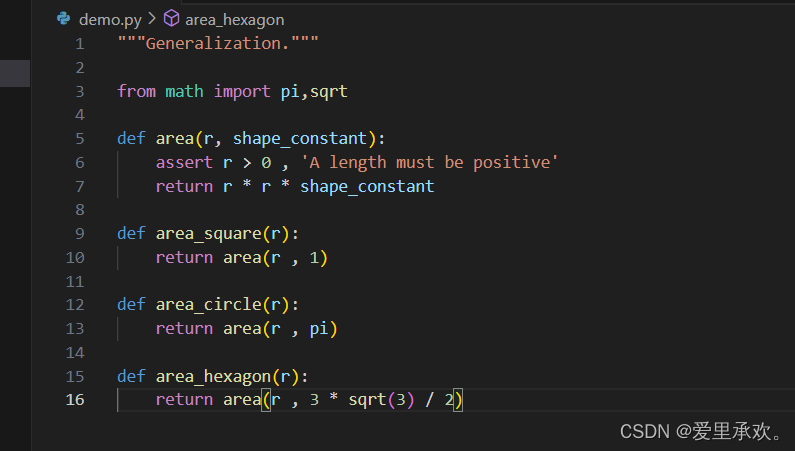

测试一个函数就是去验证函数的行为是否符合预期。现在我们的函数语句已经足够复杂,所以我们需要开始测试我们的实现的函数功能。
测试是一种系统地执行验证的机制。它通常采用另一个函数的形式,其中包含对一个或多个对被测试函数的调用样例,然后根据预期结果验证其返回值。与大多数旨在通用的函数不同,测试需要选择特定参数值,并使用它们验证函数调用。测试也可用作文档:去演示如何调用函数,以及如何选择合适的参数值。
断言(Assertions):程序员使用 assert 语句来验证是否符合预期,例如验证被测试函数的输出。assert 语句在布尔上下文中有一个表达式,后面是一个带引号的文本行(单引号或双引号都可以,但要保持一致),如果表达式的计算结果为假值,则显示该行。
>>> assert fib(8) == 13, '第八个斐波那契数应该是 13'当被断言的表达式的计算结果为真值时,执行断言语句无效。而当它是假值时,assert 会导致错误,使程序停止执行。
fib 的测试函数应该测试几个参数,包括 n 的极限值。
>>> def fib_test():
assert fib(2) == 1, '第二个斐波那契数应该是 1'
assert fib(3) == 1, '第三个斐波那契数应该是 1'
assert fib(50) == 7778742049, '在第五十个斐波那契数发生 Error'当在文件中而不是直接在解释器中编写 Python 时,测试通常是在同一个文件或带有后缀 _test.py 的相邻文件中编写的。
文档测试(Doctests):Python 提供了一种方便的方法,可以将简单的测试直接放在函数的文档字符串中。文档字符串的第一行应该包含函数的单行描述,接着是一个空行,下面可能是参数和函数意图的详细描述。此外,文档字符串可能包含调用该函数的交互式会话示例:
>>> def sum_naturals(n):
"""返回前 n 个自然数的和。
>>> sum_naturals(10)
55
>>> sum_naturals(100)
5050
"""
total, k = 0, 1
while k <= n:
total, k = total + k, k + 1
return total然后,可以通过 doctest 模块 来验证交互,如下。
>>> from doctest import testmod
>>> testmod()
TestResults(failed=0, attempted=2)如果仅想验证单个函数的 doctest 交互,我们可以使用名为 run_docstring_examples 的 doctest 函数。不幸的是,这个函数调用起来有点复杂。第一个参数是要测试的函数;第二个参数应该始终是表达式 globals() 的结果,这是一个用于返回全局环境的内置函数;第三个参数 True 表示我们想要“详细”输出:所有测试运行的目录。
>>> from doctest import run_docstring_examples
>>> run_docstring_examples(sum_naturals, globals(), True)
Finding tests in NoName
Trying:
sum_naturals(10)
Expecting:
55
ok
Trying:
sum_naturals(100)
Expecting:
5050
ok当函数的返回值与预期结果不匹配时,run_docstring_examples 函数会将此问题报告为测试失败。
当你在文件中编写 Python 时,可以通过使用 doctest 命令行选项启动 Python 来运行文件中的所有 doctest:
python3 -m doctest <python_source_file>有效测试的关键是在实现新功能后立即编写(并运行)测试。在实现之前编写一些测试也是一种很好的做法,以便在你的脑海中有一些示例输入和输出。调用单个函数的测试称为单元测试(unit test)。详尽的单元测试是良好程序设计的标志。
二、高阶函数
我们已经意识到,函数其实是一种抽象方法,它描述了与特定参数值无关的的复合操作。
>>> def square(x):
return x * x也就是说,在 square 中我们并不是在讨论一个特定数字的平方,而是在讨论一种可以获得任何数字平方的方法。当然,我们也可以在不定义这个函数的情况下,通过写下面的表达式来计算平方得到结果,从而不显式地提到 square。
>>> 3 * 3
9
>>> 5 * 5
25这种做法对于诸如 square 之类的简单计算是足够的,但对于诸如 abs 或 fib 之类的更复杂的样例就会变得很麻烦。一般来说,缺少函数定义会对我们非常不利,它会迫使我们总是工作在特定的原始操作级别(本例中为乘法),而不是更高的操作级别。我们的程序将能够计算平方,但缺少表达平方的概念的能力。
我们对强大的编程语言提出的要求之一就是能够通过将名称分配给通用模板(general patterns)来构建抽象,然后直接使用该名称进行工作。函数提供了这种能力。正如我们将在下面的示例中看到的那样,代码中重复出现了一些常见的编程模板,但它们可以与许多不同的函数一起使用。这些模板也可以通过给它们命名来进行抽象。
为了将某些通用模板表达为具名概念(named concepts),我们需要构造一种“可以接收其他函数作为参数”或“可以把函数当作返回值”的函数。这种可以操作函数的函数就叫做高阶函数(higher-order functions)。本节将会展示:高阶函数可以作为一种强大的抽象机制,来极大地提高我们语言的表达能力。
2.1、作为参数的函数
思考以下三个计算求和的函数。第一个 sum_naturals 会计算从 1 到 n 的自然数之和:
>>> def sum_naturals(n):
total, k = 0, 1
while k <= n:
total, k = total + k, k + 1
return total
>>> sum_naturals(100)
5050第二个 sum_cubes 函数会计算 1 到 n 的自然数的立方之和。
>>> def sum_cubes(n):
total, k = 0, 1
while k <= n:
total, k = total + k*k*k, k + 1
return total
>>> sum_cubes(100)
25502500
第三个 pi_sum 会计算下列各项的总和,它的值会非常缓慢地收敛(converge)到 𝜋 。
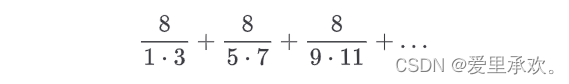
>>> def pi_sum(n):
total, k = 0, 1
while k <= n:
total, k = total + 8 / ((4*k-3) * (4*k-1)), k + 1
return total
>>> pi_sum(100)
3.1365926848388144这三个函数显然在背后共享着一个通用的模板(pattern)。它们在很大程度上是相同的,仅在名称和用于计算被加项 k 的函数上有所不同。我们可以通过在同一模板中填充槽位(slots)来生成每个函数:
def <name>(n):
total, k = 0, 1
while k <= n:
total, k = total + <term>(k), k + 1
return total
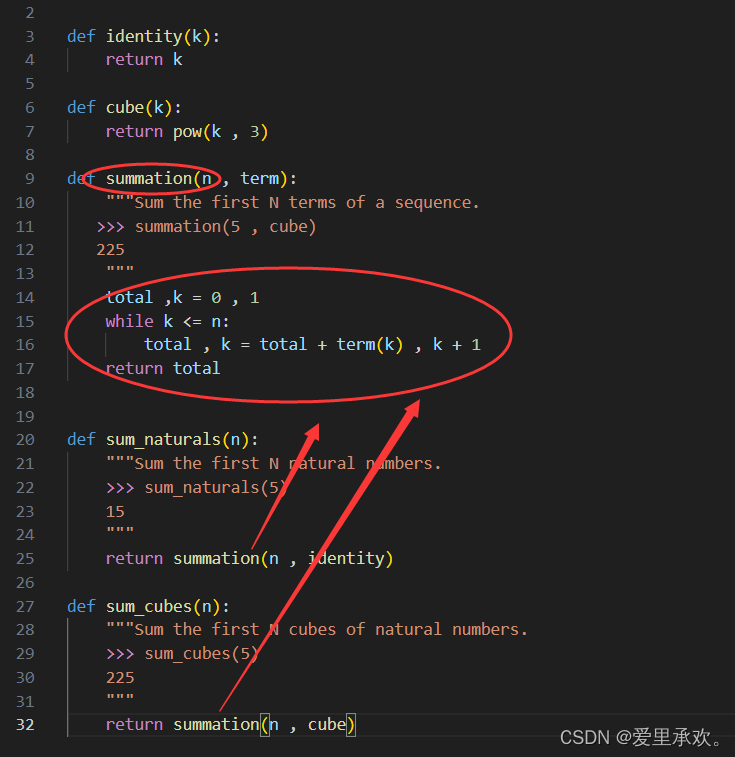
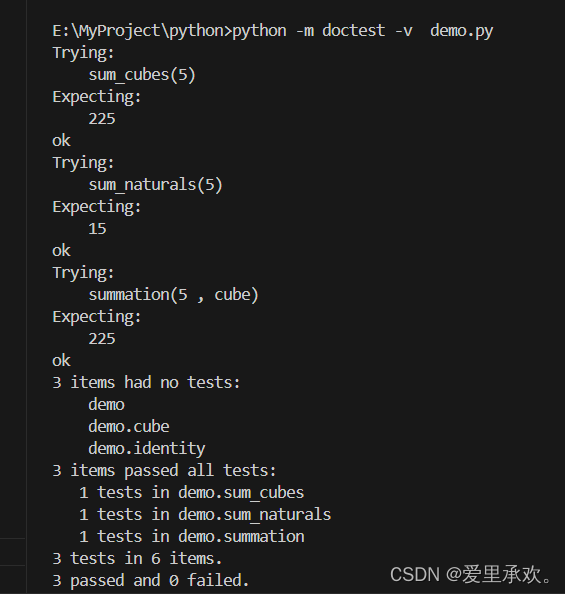
使用会返回其参数的 identity 函数,我们还可以使用完全相同的 summation 函数对自然数求和。
>>> def summation(n, term):
total, k = 0, 1
while k <= n:
total, k = total + term(k), k + 1
return total
>>> def identity(x):
return x
>>> def sum_naturals(n):
return summation(n, identity)
>>> sum_naturals(10)
55summation 函数也可以直接调用,而无需为特定的数列去定义另一个函数。
>>> summation(10, square)
385可以定义 pi_term 函数来计算每一项的值,从而使用我们对 summation 的抽象来定义 pi_sum 函数。传入参数 1e6(1 * 10^6 = 1000000 的简写)以计算 𝜋 的近似值。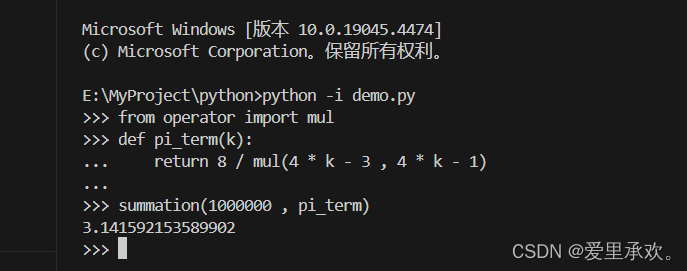
>>> def pi_term(x):
return 8 / ((4*x-3) * (4*x-1))
>>> def pi_sum(n):
return summation(n, pi_term)
>>> pi_sum(1e6)
3.1415921535899022.2、作为返回值的函数

上面这段代码我们看到,make_adder()方法返回了一个加法adder()的函数,adder()只是返回了一个数字,但是有趣的是,adder()可以使用它的名字作为形式参数,并且可以使用make_adder()周围的形式参数。
通过创建“返回值就是函数”的函数,我们可以在我们的程序中实现更强大的表达能力。带有词法作用域的编程语言的一个重要特性就是,局部定义函数在它们返回时仍旧持有所关联的环境。下面的例子展示了这一特性的作用。
一旦定义了许多简单的函数,函数组合(composition)就成为编程语言中的一种自然的组合方法。也就是说,给定两个函数 f(x) 和 g(x),我们可能想要定义 h(x) = f(g(x))。我们可以使用我们现有的工具来定义函数组合:
>>> def compose1(f, g):
def h(x):
return f(g(x))
return h2.3、嵌套定义
让我们思考一个新问题:计算一个数的平方根。在编程语言中,“平方根”通常缩写为 sqrt。重复应用以下更新,值会收敛为 a 的平方根:
>>> def average(x, y):
return (x + y)/2
>>> def sqrt_update(x, a):
return average(x, a/x)这个两个参数的更新函数与只有一个参数的 improve 函数并不兼容,还有一个问题是它只提供一次更新,但我们真正想要的是通过重复更新来求平方根。这两个问题的解决方案就是嵌套定义函数,将函数定义放在另一个函数定义内。
>>> def sqrt(a):
def sqrt_update(x):
return average(x, a/x)
def sqrt_close(x):
return approx_eq(x * x, a)
return improve(sqrt_update, sqrt_close)与局部赋值一样,局部的 def 语句只影响局部帧。被定义的函数仅在求解 sqrt 时在作用域内。而且这些局部 def 语句在调用 sqrt 之前都不会被求解,与求解过程一致。
词法作用域(Lexical scope):局部定义的函数也可以访问整个定义作用域内的名称绑定。在此示例中,sqrt_update 引用名称 a,它是其封闭函数 sqrt 的形式参数。这种在嵌套定义之间共享名称的规则称为词法作用域。最重要的是,内部函数可以访问定义它们的环境中的名称(而不是它们被调用的位置)。
我们需要实现两个扩展使环境模型启用词法作用域:
- 每个用户定义的函数都有一个父环境:定义它的环境。
- 调用用户定义的函数时,其局部帧会继承其父环境。
在调用 sqrt 之前,所有函数都是在全局环境中定义的,因此它们都有相同的父级:全局环境。相比之下,当 Python 计算 sqrt 的前两个子句时,它会创建局部环境关联的函数。
>>> sqrt(256)
16.0在这次调用中,环境首先为 sqrt 添加一个局部帧,然后求解 sqrt_update 和 sqrt_close 的 def 语句。
从现在开始我们将在环境图中的每个函数都增加一个新注释 --> 父级注释(a parent annotation)。函数值的父级是定义该函数的环境的第一帧。没有父级注释的函数是在全局环境中定义的。当调用用户定义的函数时,创建的帧与该函数具有相同的父级。
随后,名称 sqrt_update 解析为这个新定义的函数,该函数作为参数传给函数 improve 。在 improve 函数的函数体中,我们必须以 guess 的初始值 x 为 1 来调用 update 函数(绑定到 sqrt_update )。这个最后的程序调用为 sqrt_update 创建了一个环境,它以一个仅包含 x 的局部帧开始,但父帧 sqrt 仍然包含 a 的绑定。
这个求值过程中最关键的部分是将 sqrt_update 的父环境变成了通过调用 sqrt_update 创建的(局部)帧。此帧还带有 [parent=f1] 的注释。
继承环境(Extended Environments):一个环境可以由任意长的帧链构成,并且总是以全局帧结束。在举 sqrt 这个例子之前,环境最多只包含两种帧:局部帧和全局帧。通过使用嵌套的 def 语句来调用在其他函数中定义的函数,我们可以创建更长的(帧)链。调用 sqrt_update 的环境由三个帧组成:局部帧 sqrt_update 、定义 sqrt_update 的 sqrt 帧(标记为 f1)和全局帧。
sqrt_update 函数体中的返回表达式可以通过遵循这一帧链来解析 a 的值。查找名称会找到当前环境中绑定到该名称的第一个值。Python 首先在 sqrt_update 帧中进行检查 --> 不存在 a ,然后又到 sqrt_update 的父帧 f1 中进行检查,发现 a 被绑定到了 256。
因此,我们发现了 Python 中词法作用域的两个关键优势:
- 局部函数的名称不会影响定义它的函数的外部名称,因为局部函数的名称将绑定在定义它的当前局部环境中,而不是全局环境中。
- 局部函数可以访问外层函数的环境,这是因为局部函数的函数体的求值环境会继承定义它的求值环境。
这里的 sqrt_update 函数自带了一些数据:a 在定义它的环境中引用的值,因为它以这种方式“封装”信息,所以局部定义的函数通常被称为闭包(closures)。
2.4、Lambda 表达式
到目前为止,每当我们想要定义一个新函数时,都需要给它取一个名字。但是对于其他类型的表达式,我们不需要将中间值与名称相关联。也就是说,我们可以计算 a * b + c * d 而不必命名子表达式 a*b 或 c*d 或完整的表达式。在 Python 中,我们可以使用 lambda 表达式临时创建函数,这些表达式会计算为未命名的函数。一个 lambda 表达式的计算结果是一个函数,它仅有一个返回表达式作为主体。不允许使用赋值和控制语句。
>>> def compose1(f, g):
return lambda x: f(g(x))我们可以通过构造相应的英文句子来理解 lambda 表达式的结构:
lambda x : f(g(x))
"A function that takes x and returns f(g(x))"lambda 表达式的结果称为 lambda 函数(匿名函数)。它没有固有名称(因此 Python 打印 <lambda> 作为名称),但除此之外它的行为与任何其他函数都相同。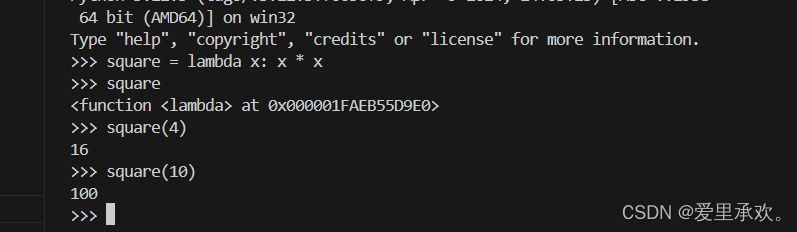
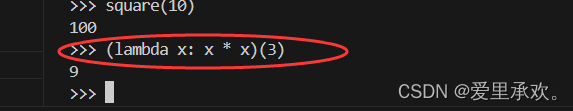
>>> s = lambda x: x * x
>>> s
<function <lambda> at 0xf3f490>
>>> s(12)
144一些程序员认为,使用 lambda 表达式中的匿名函数可以让代码更简洁、更直观。然而,尽管复合 lambda 表达式很简洁,但它是出了名的难以辨认。以下的代码虽然没有错误,但很多程序员却很难快速理解它。
>>> compose1 = lambda f,g: lambda x: f(g(x))一般来说,Python style 更喜欢使用明确的 def 语句而不是 lambda 表达式,但在需要简单函数作为参数或返回值的情况下可以使用它们。
这样的风格规则只是指导方针,你可以按照自己的方式编程。但是,在编写程序时,请考虑今后可能阅读你的程序的受众。如果你能够使程序更易于理解,那么你就是在帮助那些人。
术语 lambda 是历史上的偶然事件,它源于书面数学符号与早期排版系统的不兼容性。
It may seem perverse to use lambda to introduce a procedure/function.
The notation goes back to Alonzo Church, who in the 1930's started with a "hat" symbol, he wrote the square function as "ŷ . y × y".
But frustrated typographers moved the hat to the left of the parameter and changed it to a capital lambda: "Λ y . y × y";
From there the capital lambda was changed to lowercase, and now we see "λ y . y × y" in math books and
(lambda (y) (* y y))in Lisp.— Peter Norvig (norvig.com/lispy2.html)
尽管其词源不寻常,但是 lambda 表达式和对应的函数应用的形式语言 --> λ 演算(lambda calculus)是计算机科学中的基本概念,不仅是被 Python 编程社区广泛使用。
上图是def和lambda的一个不同,当我们查看函数值的时候会发现,lambda的功能依旧是匿名的,而square绑定的功能就是square。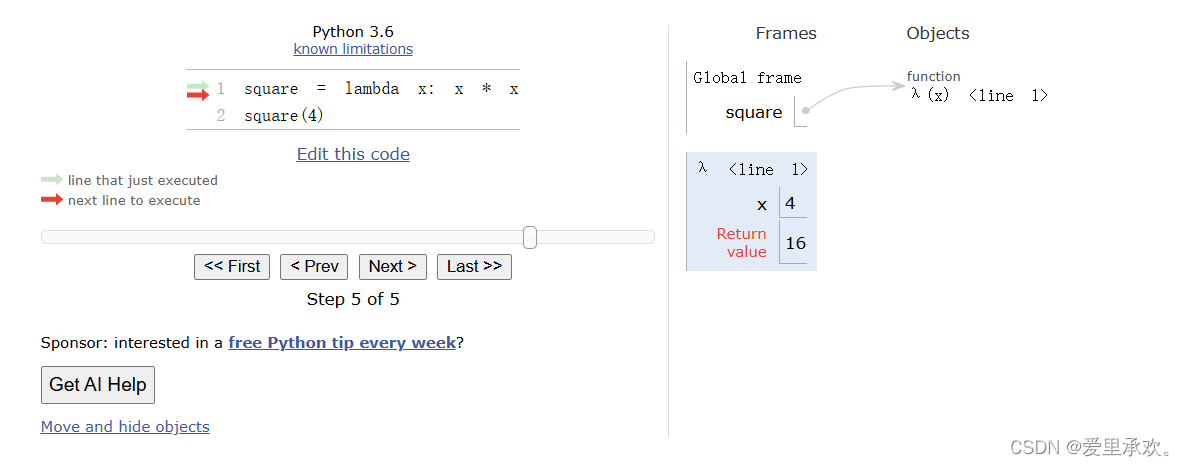
借助调试器,我们看到lambda,将名称square绑定到一个函数,square的功能写的仍旧是λ,当我们调用的时候,将所有的信息复制到一个λ框架中,而在def中则不同。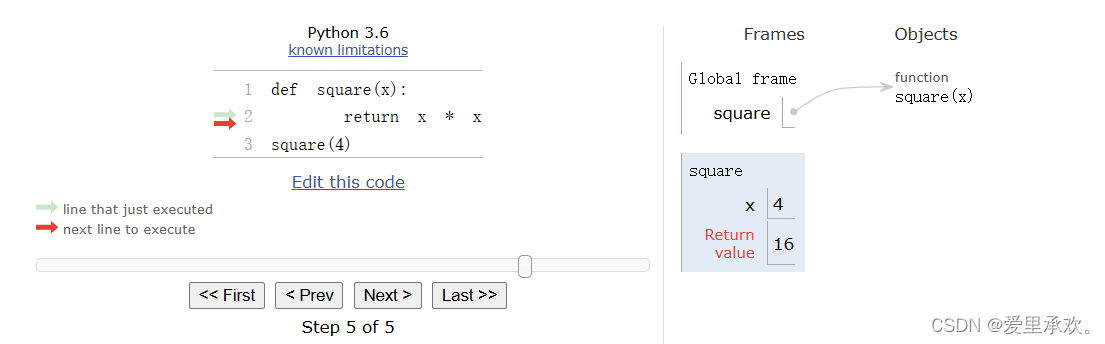
2.5、示例:牛顿法
首先,我们写一个搜索数字的函数,这是一个高阶函数,它需要另一个函数,不断尝试所有整数,一直向上,如果函数中针对于函数f的x是真值,则代表我们找到想要的数字。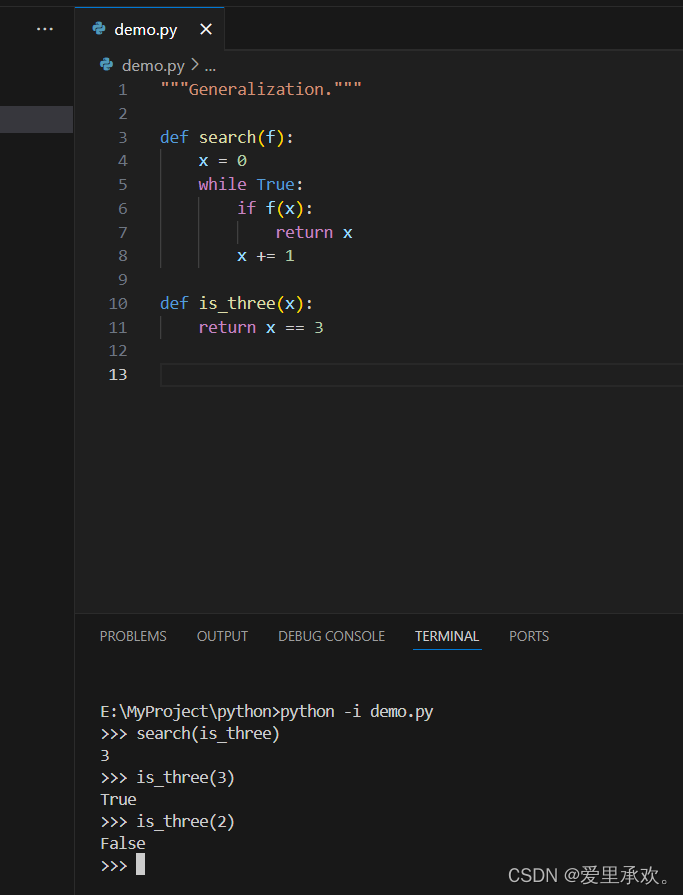
上面的函数在is_three传入的时候成功返回了3,因为3便是函数is_three的真值,而2/其它则不是。
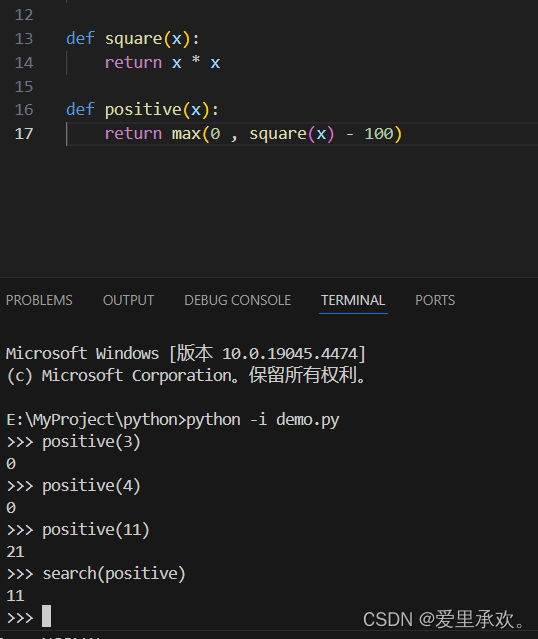
上面有两个函数,一个是平方函数,另一个是想要搜索到的x值是0和x的平方-100之间的最大值。我们仅是利用了0是假值,而其他数字是真值,以便达到返回此语句。
你还可以计算反函数,将sqrt定义成square的反函数,可以得出sqrt是平方根,square是平方函数。但是此平方根只适用于整数。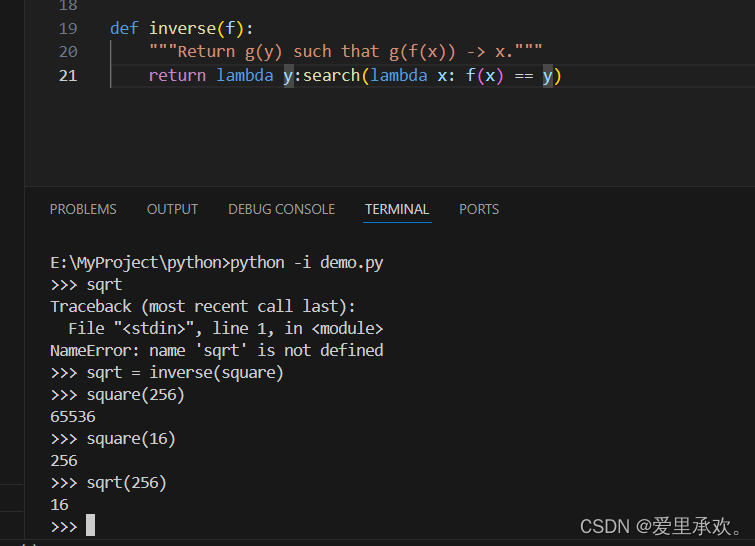
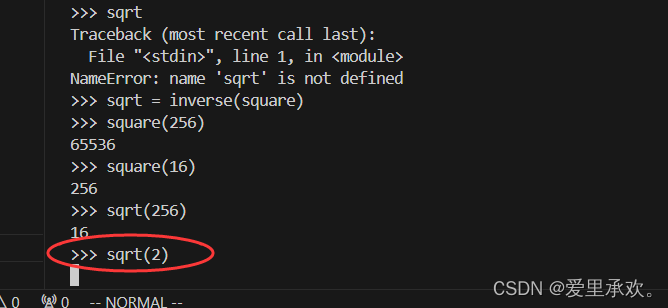
我们还可以写出更短的搜索函数版本:
牛顿法(Newton's method)是一种经典的迭代方法,用于查找返回值为 0 的数学函数的参数。这些值(参数)称为函数的零点(Zeros)。找到函数的零点通常等同于解决了其他一些有趣的问题,例如求平方根。
牛顿法是一种迭代改进算法:它会对所有可微(differentiable)函数的零点的猜测值进行改进,这意味着它可以在任意点用直线进行近似处理。牛顿的方法遵循这些线性近似(linear approximations)来找到函数零点。
试想一条穿过点 (𝑥,𝑓(𝑥)) 的直线与函数 𝑓(𝑥) 在该点拥有相同的斜率。这样的直线称为切线(tangent),它的斜率我们称为 𝑓 在 𝑥 处的导数(derivative)。
这条直线的斜率是函数值变化量与函数自变量的比值。所以,按照 𝑓(𝑥) 除以这个斜率来平移 𝑥 ,就会得到切线到达 0 时的自变量的值。
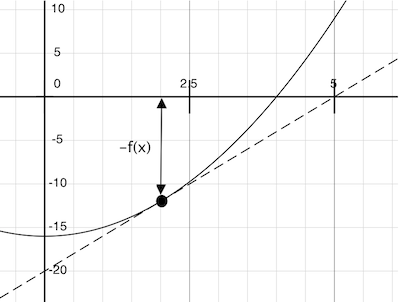
newton_update 表示函数 𝑓 及其导数 d𝑓 沿着这条切线到 0 的计算过程。
>>> def newton_update(f, df):
def update(x):
return x - f(x) / df(x)
return update最后,我们可以使用 newton_update、improve 算法以及比较 𝑓(𝑥) 是否接近 0 来定义 find_root 函数。
>>> def find_zero(f, df):
def near_zero(x):
return approx_eq(f(x), 0)
return improve(newton_update(f, df), near_zero)计算根:我们可以使用牛顿法来计算任意次方根,a 的 n 次方根就是使得 𝑥⋅𝑥⋅𝑥⋯𝑥=𝑎 的重复 n 次的 𝑥 的值,例如:
- 64 的平方根是 8, 因为 8⋅8=64
- 64 的三次方根是 4, 因为 4⋅4⋅4=64
- 64 的六次方根是 2,因为 2⋅2⋅2⋅2⋅2⋅2=64
我们可以使用牛顿法根据以下观察结果来计算根:
- 64 的平方根 (写作 64 ) 是使得 𝑥2−64=0 的 𝑥 的值
- 推广来说,a 的 n 次方根 (写作 𝑎𝑛 ) 是使得 𝑥𝑛−𝑎=0 的 𝑥 的值
如果我们可以找到最后一个方程的零点,那么我们就可以计算出 n 次方根。通过绘制 n 等于 2、3 和 6,a 等于 64 的曲线,我们可以将这种关系可视化。
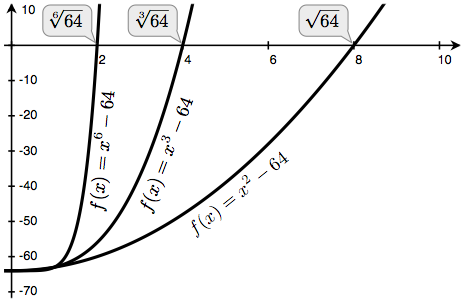
我们首先通过定义 𝑓 和它的导数 d𝑓 来实现 square_root 函数,使用微积分中的知识,𝑓(𝑥)=𝑥2−𝑎 的导数是线性方程 d𝑓(𝑥)=2𝑥。
>>> def square_root_newton(a):
def f(x):
return x * x - a
def df(x):
return 2 * x
return find_zero(f, df)
>>> square_root_newton(64)
8.0推广到 n 次方根,我们可以得到 𝑓(𝑥)=𝑥𝑛−𝑎 和它的导数 d𝑓(𝑥)=𝑛𝑥𝑛−1。
>>> def power(x, n):
"""返回 x * x * x * ... * x,n 个 x 相乘"""
product, k = 1, 0
while k < n:
product, k = product * x, k + 1
return product
>>> def nth_root_of_a(n, a):
def f(x):
return power(x, n) - a
def df(x):
return n * power(x, n-1)
return find_zero(f, df)
>>> nth_root_of_a(2, 64)
8.0
>>> nth_root_of_a(3, 64)
4.0
>>> nth_root_of_a(6, 64)
2.0所有这些计算中的近似误差都可以通过将 approx_eq 中的公差 tolerance 改为更小的数字来减小。
当你使用牛顿法时,要注意它并不总是收敛(converge)的。improve 的初始猜测必须足够接近零,并且必须满足有关函数的各种条件。尽管有这个缺点,牛顿法仍是一种用于求解微分方程的强大的通用计算方法。现代计算机技术中的对数和大整数除法的快速算法,都采用了该方法的变体。