支持向量机
- 参数模型
- 对分布需要假设（这也是与非参数模型的区别之一）
- 间隔最大化，形式转化为凸二次规划问题
最大化间隔
间隔最大化是意思：对训练集有着充分大的确信度来分类训练数据，最难以分的点也有足够大的信度将其分开
间隔最大化的分离超平面的的求解怎么求呢？
最终的方法如下
1.线性可分的支持向量机的优化目标
其实就是找得到分离的的超平面
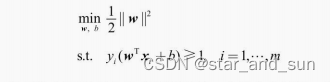
求得参数w和b的值就可以了
注意，最大间隔分离超平面是唯一的，间隔叫硬间隔
1.1支持向量
对于一个样本，要么对应的参数a为0，要么与超平面的间隔为γ，将这些与超平面距离最小的向量x称为支持向量
也就是训练点到分离超平面距离最近的样本点就是支持向量
2. 线性支持向量机的目标函数
线性可分的问题对不可分不适用，因此需要将硬间隔改为软间隔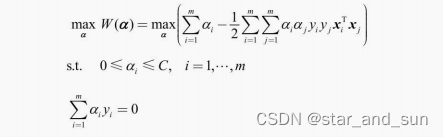
这里的a是待求解的参数，梯度参数量是和规模m相关，数据的规模增大时，参数量也增多。 
线性支持向量机包括了线性可分支持向量机
序列最小优化算法（SMO）
我们只需要用支持向量来进行分类，这样子减少了复杂度和时间消耗，但是优势不明显，因为参数a的求解需要的时间也很大，所以用到了序列最小优化算法来解决这个问题。
思想：同时优化所有的参数比较困难，因此选择部分参数来优化，选择两个固定其他的，然后再选两个固定其他的一直循环，直到更新参数的变化小于某个值就可以终止，或者固定迭代次数。
线性可分的代码实例
采用的linear.csv数据
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from tqdm import tqdm, trange
data = np.loadtxt('./data/linear.csv', delimiter=',')
print('数据集大小：', len(data))
x = data[:, :2]
y = data[:, 2]
# 数据集可视化
plt.figure()
plt.scatter(x[y == -1, 0], x[y == -1, 1], color='red', label='y=-1')
plt.scatter(x[y == 1, 0], x[y == 1, 1], color='blue', marker='x', label='y=1')
plt.xlabel(r'$x_1$')
plt.ylabel(r'$x_2$')
plt.legend()
plt.show()
#%%
def SMO(x, y, ker, C, max_iter):
'''
SMO算法
x，y：样本的值和类别
ker：核函数，与线性回归中核函数的含义相同
C：惩罚系数
max_iter：最大迭代次数
'''
# 初始化参数
m = x.shape[0]
alpha = np.zeros(m)
# 预先计算所有向量的两两内积，减少重复计算
K = np.zeros((m, m))
for i in range(m):
for j in range(m):
K[i, j] = ker(x[i], x[j])
for l in trange(max_iter):
# 开始迭代
for i in range(m):
# 有m个参数，每一轮迭代中依次更新
# 固定参数alpha_i与另一个随机参数alpha_j，并且保证i与j不相等
j = np.random.choice([l for l in range(m) if l != i])
# 用-b/2a更新alpha_i的值
eta = K[j, j] + K[i, i] - 2 * K[i, j] # 分母
e_i = np.sum(y * alpha * K[:, i]) - y[i] # 分子
e_j = np.sum(y * alpha * K[:, j]) - y[j]
alpha_i = alpha[i] + y[i] * (e_j - e_i) / (eta + 1e-5) # 防止除以0
zeta = alpha[i] * y[i] + alpha[j] * y[j]
# 将alpha_i和对应的alpha_j保持在[0,C]区间
# 0 <= (zeta - y_j * alpha_j) / y_i <= C
if y[i] == y[j]:
lower = max(0, zeta / y[i] - C)
upper = min(C, zeta / y[i])
else:
lower = max(0, zeta / y[i])
upper = min(C, zeta / y[i] + C)
alpha_i = np.clip(alpha_i, lower, upper)
alpha_j = (zeta - y[i] * alpha_i) / y[j]
# 更新参数
alpha[i], alpha[j] = alpha_i, alpha_j
return alpha
#%%
# 设置超参数
C = 1e8 # 由于数据集完全线性可分，我们不引入松弛变量
max_iter = 1000
np.random.seed(0)
alpha = SMO(x, y, ker=np.inner, C=C, max_iter=max_iter)
#%%
# 用alpha计算w，b和支持向量
sup_idx = alpha > 1e-5 # 支持向量的系数不为零
print('支持向量个数：', np.sum(sup_idx))
w = np.sum((alpha[sup_idx] * y[sup_idx]).reshape(-1, 1) * x[sup_idx], axis=0)
wx = x @ w.reshape(-1, 1)
b = -0.5 * (np.max(wx[y == -1]) + np.min(wx[y == 1]))
print('参数：', w, b)
#%%
# 绘图
X = np.linspace(np.min(x[:, 0]), np.max(x[:, 0]), 100)
Y = -(w[0] * X + b) / (w[1] + 1e-5)
plt.figure()
plt.scatter(x[y == -1, 0], x[y == -1, 1], color='red', label='y=-1')
plt.scatter(x[y == 1, 0], x[y == 1, 1], marker='x', color='blue', label='y=1')
plt.plot(X, Y, color='black')
# 用圆圈标记出支持向量
plt.scatter(x[sup_idx, 0], x[sup_idx, 1], marker='o', color='none',
edgecolor='purple', s=150, label='support vectors')
plt.xlabel(r'$x_1$')
plt.ylabel(r'$x_2$')
plt.legend()
plt.show()
线性不可分的
# 从sklearn.svm中导入SVM分类器
from sklearn.svm import SVC
data1=np.loadtxt('./data/spiral.csv',delimiter=',')
x=data[:,:2]
y=data[:,2]
# 定义SVM模型，包括定义使用的核函数与参数信息
model = SVC(kernel='rbf', gamma=50, tol=1e-6)
model.fit(x, y)
# 绘制结果
fig = plt.figure(figsize=(6,6))
G = np.linspace(-1.5, 1.5, 100)
G = np.meshgrid(G, G)
X = np.array([G[0].flatten(), G[1].flatten()]).T # 转换为每行一个向量的形式
Y = model.predict(X)
Y = Y.reshape(G[0].shape)
plt.contourf(G[0], G[1], Y, cmap=cmap, alpha=0.5)
# 绘制原数据集的点
plt.scatter(x[y == -1, 0], x[y == -1, 1], color='red', label='y=-1')
plt.scatter(x[y == 1, 0], x[y == 1, 1], marker='x', color='blue', label='y=1')
plt.xlabel(r'$x_1$')
plt.ylabel(r'$x_2$')
plt.legend()
plt.show()
