目录
常见的位运算的操作总结
①基础位操作
②给一个数n,确定它的二进制表示中的第x位是0还是1
③将一个数n的二进制表示的第x位修改成1
④将一个数n的二进制表示的第x位修改成0
⑤位图的思想
⑥提取一个数n二进制表示中最右侧的1
⑦干掉一个数n二进制表示中最右侧的1
⑧位运算的优先级
⑨异或(^)运算的运算律
题目一:位1的个数
题目二:比特位计数
题目三:汉明距离
题目四:只出现一次的数字I
题目五:只出现一次的数字III
题目六:判断字符是否唯一
题目七:丢失的数字
题目八:两整数之和
题目九:只出现一次的数字II
题目十:消失的两个数字
常见的位运算的操作总结
在讲解位运算题目前,先将常见的位运算的操作做以总结
①基础位操作
有以下几种:
<<(左移) >>(右移) ~(按位取反) &(按位与) |(按位或) ^(按位异或)
左移<<和右移>>:将这个比特位向左或向右移动
按位取反~:将所有比特位全部取反,1变0,0变1
按位与&:有0为0
按位或|:有1为1
按位异或^:相同为0相异为1或无进位相加
无进位相加指不看进的位,只看保留位,例如1+1等于2,二进制中会进位1,余0,不看进位,只看留下的0
②给一个数n,确定它的二进制表示中的第x位是0还是1
我们假设二进制表示中,最右边的数为最低位
为了确定二进制某一位是0还是1,只需要将这一位&1即可
而为了将这一位&1,需要将该位右移x位,这样就可以将第x位移动到最低位的位置,此时按位与1,即可将这个数的第x位与1进行按位与
(n >> x) & 1
上式最终结果如果是0,第x位就是0;如果是1,第x位就是1
③将一个数n的二进制表示的第x位修改成1
将一个数变为1,也就是将这个数按位或1即可
那么将这个数n的第x位按位或1,其余位都不变,也就是将1左移x位,其余位都是0,此时再按位或即可:
n |= (1 << x)
④将一个数n的二进制表示的第x位修改成0
将一个数修改为0,也就是需要按位与0,但是只是修改第x位,那么在按位与时,其他无关位应该是1,例如:
想让下面的红色的1变为0,只需要按位与下面的绿色二进制表示的数即可:
0 1 1 1 0 0 1 0 0 0
1 1 1 1 1 1 0 1 1 1 &
此时的结果就为:
0 1 1 1 0 0 0 0 0 0
成功将该位变成0,其他位不变
那么想要形成这个绿色的二进制形式,只需要将1左移x位:
0 0 0 0 0 0 1 0 0 0
再按位取反,就得到了:
1 1 1 1 1 1 0 1 1 1
所以公式为:
n &= (~(1 << x))
⑤位图的思想
位图在前面是说过的
其实就是哈希表的思想,方便我们进行查找
只不过位图是每一位是一个比特位来记录信息,比特位为0或为1,来记录不同的情况
⑥(常用)提取一个数n二进制表示中最右侧的1
意思就是如果有一个二进制数表示如下:
0 1 1 1 0 0 1 0 1 0 0 0
我们需要提取出这个二进制数n最右侧的这个红色的1
只需要进行 n & -n 就能得到,理由如下
这个数为:
0 1 1 1 0 0 1 0 1 0 0 0
那么一个数n变为-n,需要取反再+1,也就是先取反,变为:
1 0 0 0 1 1 0 1 0 1 1 1
再+1,最后变为:
1 0 0 0 1 1 0 1 1 0 0 0
我们可以发现,上面的绿色区域就是我们所需要的最右边的1及其右边其他的数,而左侧棕黄色的数就是最右侧的1左边所有数
绿色区域的数与原来相比没有发生变化,棕色区域则全部取反了,此时将原来的数n与新变的数-n按位与,就可以将除了最右侧的1之外的其他所有数全变为0,从而得到最终结果,得到了:
0 0 0 0 0 0 0 0 1 0 0 0
⑦(常用)干掉一个数n二进制表示中最右侧的1
想要干掉二进制表示的最右侧的1,进行的操作是:n & (n-1)
有一个二进制数n表示如下:
0 1 1 1 0 0 1 0 1 0 0 0
将红色的1干掉,只需将上述的n-1,变为:
0 1 1 1 0 0 1 0 0 1 1 1
此时我们可以发现,最右侧的1左边的数都没有发生变化, 而最右侧的1及其左边的数全部按位取反了,此时 n & (n-1)就变为了:
0 1 1 1 0 0 1 0 0 0 0 0
相当于将最右侧的1干掉了
原理其实很简单,因为最右侧的1右边都是0,此时-1的话,会一直向前面借位,直到遇到最右侧的第一个1,此时这个1遇到前面的借位自然就变为0了
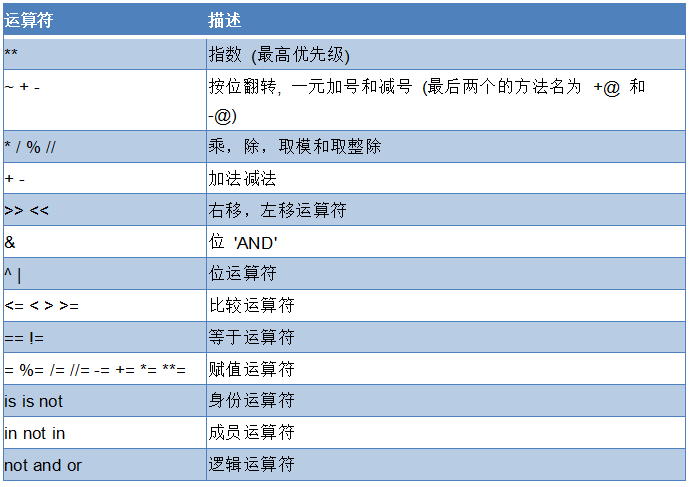
⑧位运算的优先级
因为各种符号的优先级我们并不能特别清楚的记忆,那么这里就需要注意:
能加括号的就加括号,这样就不需要考虑优先级问题了
⑨异或(^)运算的运算律
a ^ 0 = a
a ^ a = 0
a ^ b ^ c = a ^ (b ^ c)
第三个规律也就是告诉我们,异或符合交换律和结合律
结合规律二可以知道,如果出现了偶数次,异或就为0,如果出现了基数次,异或后就为它本身
题目一:位1的个数
编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中
设置位的个数(也被称为汉明重量)。
示例 1:
输入:n = 11
输出:3
解释:输入的二进制串 1011 中,共有 3 个设置位。
示例 2:
输入:n = 128 输出:1 解释:输入的二进制串 10000000 中,共有 1 个设置位。
示例 3:
输入:n = 2147483645 输出:30 解释:输入的二进制串 11111111111111111111111111111101 中,共有 30 个设置位。
提示:
1 <= n <= 231 - 1
此题可以使用for循环,判断32次比特位是否1,这个方法比较简单,比较慢,就不说明了,代码如下:
class Solution {
public:
int hammingWeight(int n) {
int num = 0;
for(int i = 0; i < 32; i++)
if(n & (1 << i)) num++;
return num;
}
};此题更好的解法是位运算,因为计算机中位运算是最快的
用到了上述第七个位运算方法的总结,干掉二进制中的最右侧的1,代码如下:
class Solution {
public:
int hammingWeight(int n) {
int num = 0;
while(n)
{
n &= (n-1);
num++;
}
return num;
}
};题目二:比特位计数
给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
示例 1:
输入:n = 2 输出:[0,1,1] 解释: 0 --> 0 1 --> 1 2 --> 10
示例 2:
输入:n = 5 输出:[0,1,1,2,1,2] 解释: 0 --> 0 1 --> 1 2 --> 10 3 --> 11 4 --> 100 5 --> 101
提示:
0 <= n <= 105
同样,此题使用上述第七个位运算方法的总结,干掉二进制中的最右侧的1,每次干掉一次右侧的1,直到这个数为0,就说明数完了1的数量
代码如下:
class Solution {
public:
vector<int> countBits(int n) {
vector<int> v;
for(int i = 0; i <= n; i++)
{
int tmp = i, num = 0;
while(tmp)
{
tmp &= (tmp - 1);
num++;
}
v.push_back(num);
}
return v;
}
};题目三:汉明距离
两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。
给你两个整数 x 和 y,计算并返回它们之间的汉明距离。
示例 1:
输入:x = 1, y = 4
输出:2
解释:
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
上面的箭头指出了对应二进制位不同的位置。
示例 2:
输入:x = 3, y = 1 输出:1
提示:
0 <= x, y <= 231 - 1
求两个数二进制中不同位的个数,其实就是将这两个数按位异或,再计算有几个1的问题,还是参照上述的第七个方法,每次干掉最右边的一个1,直到这个数为0为止
代码如下:
class Solution {
public:
int hammingDistance(int x, int y) {
int s = x ^ y, num = 0;
while(s)
{
s &= (s-1);
num++;
}
return num;
}
};题目四:只出现一次的数字I
给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。
示例 1 :
输入:nums = [2,2,1] 输出:1
示例 2 :
输入:nums = [4,1,2,1,2] 输出:4
示例 3 :
输入:nums = [1] 输出:1
提示:
1 <= nums.length <= 3 * 104-3 * 104 <= nums[i] <= 3 * 104- 除了某个元素只出现一次以外,其余每个元素均出现两次。
此题很明显考察的是异或运算符的使用,考察的是上述的第九个异或运算的运算律,a ^ a = 0,出现两次的数异或就为0
代码如下:
class Solution {
public:
int singleNumber(vector<int>& nums) {
int ret = 0;
for(auto& it : nums) ret ^= it;
return ret;
}
};题目五:只出现一次的数字III
给你一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。
你必须设计并实现线性时间复杂度的算法且仅使用常量额外空间来解决此问题。
示例 1:
输入:nums = [1,2,1,3,2,5] 输出:[3,5] 解释:[5, 3] 也是有效的答案。
示例 2:
输入:nums = [-1,0] 输出:[-1,0]
示例 3:
输入:nums = [0,1] 输出:[1,0]
提示:
2 <= nums.length <= 3 * 104-231 <= nums[i] <= 231 - 1- 除两个只出现一次的整数外,
nums中的其他数字都出现两次
此题比上面那一题难一些,上面那一题是只有一个出现一次的数,而此题是有两个出现一次的数
同样,先将全部的数异或一遍,此时所有出现两次的数字都别抵消了,剩下的这个ret就是两个只出现一次的数异或出来的
由于这两个只出现一次的数不相同,所以如果ret的某一位的比特位为1,则说明这两个出现一次的数在该比特位上的数字是不同的
所以利用这一点,将数组分为两个组,一个组这个比特位为0,一个组这个比特位为1,这时的问题就转换成了上一题的情况,其他数字都出现两次,只有一个数字出现一次,此时这两组数字分别异或,得到的就是两个只出现一次的数字
代码如下:
class Solution {
public:
vector<int> singleNumber(vector<int>& nums) {
unsigned int ret = 0;//防溢出
for(auto& it : nums) ret ^= it;
int lowbit = ret & -ret; //提取最右侧的1
int group1 = 0, group2 = 0;
for(auto& it : nums)
{
if(it & lowbit) group1 ^= it;
else group2 ^= it;
}
return {group1, group2};
}
};题目六:判断字符是否唯一
实现一个算法,确定一个字符串 s 的所有字符是否全都不同。
示例 1:
输入: s = "leetcode"
输出: false
示例 2:
输入: s = "abc"
输出: true
限制:
0 <= len(s) <= 100s[i]仅包含小写字母- 如果你不使用额外的数据结构,会很加分。
这道题有非常多的解法, 例如:
解法一:哈希表
遍历一遍字符串,每次都判断该字符是否在哈希表中,如果不在就放入哈希表中,如果在就返回false,如果直到最后一个字符,都发现没在哈希表中,此时就返回true
哈希表的时间复杂度是O(N),空间复杂度也是O(N)的,这里的哈希表可以不使用unordered_map,可以使用数组代替
代码如下:
class Solution {
public:
bool isUnique(string astr) {
int hash[26] = {0};
for(auto& it : astr)
{
if(hash[it - 'a'] != 0) return false;
hash[it - 'a']++;
}
return true;
}
};解法二:位图
可以借助位图的思想,单独的int变量就有32位比特位,英文字符总共才26位,那么我们就可以从右向左,第一个比特位代表a,第二个比特位代表b ....,只需要用到26个比特位,甚至连一个int的空间都用不完,相比于上述的int类型的数组hash,提升了非常多
每一个比特位要么是0要么是1,0表示字符没有出现过,1表示字符出现过
这里有一个优化点,鸽巢原理,也就是英文字母总共才26个,如果这个字符串长度超过26,就说明肯定是有重复字符的,所以这时直接返回false即可,就不需要进行下面的判断了
代码如下:
class Solution {
public:
bool isUnique(string astr) {
if(astr.size() > 26) return false;//鸽巢原理优化
int bitset = 0;
for(auto& ch : astr)
{
int i = ch - 'a';
//判断字符是否出现过
if(bitset & (1 << i)) return false;
//把当前字符加入位图中
bitset |= (1 << i);
}
return true;
}
};题目七:丢失的数字
给定一个包含 [0, n] 中 n 个数的数组 nums ,找出 [0, n] 这个范围内没有出现在数组中的那个数。
示例 1:
输入:nums = [3,0,1] 输出:2 解释:n = 3,因为有 3 个数字,所以所有的数字都在范围 [0,3] 内。2 是丢失的数字,因为它没有出现在 nums 中。
示例 2:
输入:nums = [0,1] 输出:2 解释:n = 2,因为有 2 个数字,所以所有的数字都在范围 [0,2] 内。2 是丢失的数字,因为它没有出现在 nums 中。
示例 3:
输入:nums = [9,6,4,2,3,5,7,0,1] 输出:8 解释:n = 9,因为有 9 个数字,所以所有的数字都在范围 [0,9] 内。8 是丢失的数字,因为它没有出现在 nums 中。
示例 4:
输入:nums = [0] 输出:1 解释:n = 1,因为有 1 个数字,所以所有的数字都在范围 [0,1] 内。1 是丢失的数字,因为它没有出现在 nums 中。
丢失的数字是有很多种方法解决的:
解法一:排序
先将数组排序,再判断缺失哪一个数字
这个解法的时间复杂度为O(N*logN)
代码如下:
class Solution {
public:
int missingNumber(vector<int>& nums) {
int n = nums.size();
sort(nums.begin(), nums.end());
for(int i = 0; i < n; i++)
{
if(nums[i] != i) return i;
}
return n;
}
};解法二:哈希表
将有的数字全部映射到数组中,最后再按顺序遍历一遍,哪个位置的数组为0,就说明缺失了哪个数字
这个解法,时间复杂度是O(N),空间复杂度也是O(N)
代码如下:
class Solution {
public:
int missingNumber(vector<int>& nums) {
int n = nums.size(), num = 0;
int hash[10000] = {0};
for(auto& it : nums) hash[it]++;
for(int i = 0; i < n+1; i++)
{
if(hash[i] == 0) num = i;
}
return num;
}
};解法三:高斯求和
也就是将原本的数组知道首项和末项,可以利用(首项 + 末项) * 项数 / 2,再把给的数组中的数依次减去,最后剩余的就是缺失的数字
这个解法的时间复杂度是O(N),空间复杂度是O(1)
class Solution {
public:
int missingNumber(vector<int>& nums) {
int n = nums.size();
int sum = (0 + n) * (n+1) / 2;
for(auto& it : nums) sum -= it;
return sum;
}
};解法四:位运算
使用异或运算,将数组中所有的数字都异或一遍,再将原本完整的数组中的数字再异或一遍,因为相同的数字异或会变为0,最后剩下的就是缺失的数字
位运算的时间复杂度为O(N),空间复杂度为O(1)
代码如下:
class Solution {
public:
int missingNumber(vector<int>& nums) {
int n = nums.size(), ret = 0;
for(auto& it : nums) ret ^= it;
for(int i = 0; i < n+1; i++) ret ^= i;
return ret;
}
};题目八:两整数之和
给你两个整数 a 和 b ,不使用 运算符 + 和 - ,计算并返回两整数之和。
示例 1:
输入:a = 1, b = 2 输出:3
示例 2:
输入:a = 2, b = 3 输出:5
这道题要求不使用运算符 + 和 - ,计算两整数之和
很明显隐藏条件就是让我们使用位运算进行计算
我们之前说过,异或运算就是无进位相加,无进位相加指的就是不看进的位,只看留下的位
那么我们现在使用异或运算,就需要关注之前没有关注的进位,那么进位怎么得到呢,仔细想一想,是不是两个数同一个比特位都是1,此时相加才会进位
所以我们可以通过按位与的方式,找到同为1的位置,知道这些同为1的位置相加是需要进位的,又因为进位是向左进位的,所以此时再将按位与后的二进制数左移一位,得到了进位后的位置
下面举例具体说明:
假设a是22,b是11,a + b = 33,也就是0 0 1 0 0 0 0 1

先按位异或,得到留下的数字:

我们发现,一位为0,另一位为1的时候,异或结果为1,而同为1时,由于异或是无进位相加,所以该位为0,此时我们需要将两个数按位与,并向左移一位,得到进位的值

此时将异或的二进制数赋值给a,进位的二进制数赋值给b,进行无进位相加,也就是相异或,得:

接着继续向后计算,上述情况的整体运算过程如下所示:

由上图所示,将a和b先按位异或得到一个值,将这个值赋值给a
再将 (a&b)>>1 得到一个值,将这个值赋值给b
如果这里的 a&b 不等于0,那就继续执行上述 a^b 的操作,直到某一次 a&b 等于0停止,此时的a值就是最终的结果
如上图所示,a原本是10110 = 22,b原本是1011 = 11,a+b = 33
最终得到的结果100001 = 33,结果是正确的
代码如下:
class Solution {
public:
int getSum(int a, int b) {
int tmpa = a, tmpb = b;
while(b)
{
int tmpa = a ^ b;
int tmpb = (a & b) << 1;
a = tmpa;
b = tmpb;
}
return a;
}
};题目九:只出现一次的数字II
给你一个整数数组 nums ,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。
示例 1:
输入:nums = [2,2,3,2] 输出:3
示例 2:
输入:nums = [0,1,0,1,0,1,99] 输出:99
这道题是只出现一次的数字的另一个版本,也是有多种解法的,如下所示:
解法一:排序
先将数组中的数字排序,给定src和des两个下标,如果相等des++,如果不相等,判断是否相差1,如果相差1,就说明src指向的元素就是所求元素,因为如果是3个相同的元素,在src和des出现不同时,是相差3的,所以如果相差1,就return即可
class Solution
{
public:
int singleNumber(vector<int>& nums)
{
sort(nums.begin(),nums.end());
int src = 0,des = 0;
while(des < nums.size())
{
if(nums[src] == nums[des]) des++;
else
{
if((des - src) == 1) return nums[src];
else src = des;
}
}
return nums[src];
}
};解法二:哈希表
将数组每一个元素都映射进哈希表中,每次都将哈希表中对应位置++,最后再遍历一遍数组,寻找对应位置的值为1的元素
class Solution
{
public:
int singleNumber(vector<int>& nums)
{
unordered_map<int, int> hash;
int ret = 0;
for(auto& it : nums) hash[it]++;
for(auto& it : nums)
{
if(hash[it] == 1) ret = it;
}
return ret;
}
};解法三:位运算
因为数组中的元素只有一个是出现一次,剩下都是出现3次,所以数组共有3n+1个元素,因此每个元素的每个比特位都只会有下面四种情况:
① 3n个0 + 1个0 -> 该比特位总和为 0 -> 总和 %3 结果为 0
② 3n个0 + 1个1 -> 该比特位总和为 1 -> 总和 %3 结果为 1
③ 3n个1 + 1个0 -> 该比特位总和为 3n -> 总和 %3 结果为 0
④ 3n个1 + 1个1 -> 该比特位总和为 3n+1 -> 总和 %3 结果为 1
可以发现,每一个比特位,将所有元素该比特位的值相加,再 %3,最终的结果都是这个只出现一次的数的比特位的值
所以就可以按照上述思路,代码如下:
class Solution
{
public:
int singleNumber(vector<int>& nums)
{
int ret = 0;
for(int i = 0; i < 32; i++)//依次修改ret中的每一个比特位
{
int tmp = 0;
//计算nums中所有数的第i个比特位的和
for(auto it : nums) tmp += ((it >> i) & 1);
tmp %= 3;
if(tmp == 1) ret |= (1 << i);
}
return ret;
}
};题目十:消失的两个数字
给定一个数组,包含从 1 到 N 所有的整数,但其中缺了两个数字。你能在 O(N) 时间内只用 O(1) 的空间找到它们吗?
以任意顺序返回这两个数字均可。
示例 1:
输入: [1]
输出: [2,3]
示例 2:
输入: [2,3]
输出: [1,4]
提示:
nums.length <= 30000
这道题是上面的 丢失的数字 与 只出现一次的数字III 这两道题的解体思路的合体
首先此题说明了从 1 到 N 所有的整数,其中缺了两个数字,那么可以将数字分为两组,一组是从 1 到 N,另一组是从 1 到 N 缺了两个数字
①将所有这两组数全部异或在一起,得到ret:a^b
如果将这两组合并起来,是不是就变为了:从 1 到 N 所有的整数都出现了2次,只有两个数a、b只出现了1次这个问题了
将合并后的数组一次按位异或,最终的结果是缺失的数字a和b按位异或的结果ret:a ^ b
②找到ret中,比特位为1的一位
此时就可以使用 只出现一次的数字III 这道题的思路,因为a和b是不同的数字,那么 a ^ b 的结果中比特位肯定存在1,此时提取一个只有这个比特位为1的二进制数,即:lowbit = ret & -ret
也就是说lowbit这个数,只有该比特位为一,其他比特位都为0
③根据该比特位的不同,划分为两组
将数字中的元素分为两大组,一组的数字该比特位为1,另一组的数字该比特位为0,这两个数组分别依次与其中的元素异或,异或结束后,两个组剩余的元素就是只出现一次的数字,即最终得到结果
代码如下:
class Solution {
public:
vector<int> missingTwo(vector<int>& nums) {
int n = nums.size(), ret = 0;
for(int i = 1; i <= n + 2; i++) nums.push_back(i);
// 将所有数全部异或在一起,得到 ret = a^b
for(auto it : nums) ret ^= it;
// 找到ret中,比特位为1的一位,这个数为lowbit
int lowbit = ret & -ret;
// 根据该比特位的不同,划分为两组,分别异或,得到结果
int group1 = 0, group2 = 0;
for(auto it : nums)
{
if(it & lowbit) group1 ^= it;
else group2 ^= it;
}
return {group1, group2};
}
};位运算相关习题的练习到此结束




![[FreeRTOS 基础知识] 任务调度 与 链表](https://img-blog.csdnimg.cn/direct/12fbc50d0a174fccaae4ae9eeec0c30b.png)