【力扣高频题】003.无重复字符的最长子串

news2024/10/9 0:47:22

前段时间和小米的某面试官聊天。因为我一直在做 算法文章 的更新，就多聊了几句算法方面的知识。

并且在聊天过程中获得了一个“重要情报”：只要他来面试，基本上每次的算法题，都会去考察关于 子串和子序列 的问题。

的确，如果说哪种算法更容易在面试中被考察到，子串、子序列 的问题想必能排在 数一数二 的位置上。

在之前的 「动态规划」 系列文章中，我们讲到了最长公共子序列和最长回文子序列的问题，今天我们继续来探讨力扣上一个关于子串的问题。

3.无重复字符的最长子串

给定一个字符串 s ，请你找出其中 不含有重复字符 的最长
子串的长度。

示例 1：

输入： s = “abcabcbb”

输出： 3

解释： 因为无重复字符的最长子串是 “abc”，所以其长度为 3。

示例 2:

输入： s = “bbbbb”

输出： 1

解释： 因为无重复字符的最长子串是 “b”，所以其长度为 1。

小 tips：要注意分清楚，子串和 子序列 的区别哟~

子串： 必须连续
子序列： 可以不连续

思路分析

这里回顾一个 重要思想 ，对于 子串和子序列 的题目，可以按如下方式进行思考：

考虑 以 i 位置为结尾 的情况下，答案如何选取

该思想在数组求和-2 这篇文章中也有提到哦~

因此，对于本题来说：

考虑若以每个位置作为结尾时，子串能够向前延伸多长，最长的子串长度就是我们要求的答案。

那么问题就进一步转化为：

在给定一个结尾的字符时，应该如何向前延伸呢，延伸的长度会受到哪些因素影响呢？

稍加思考：

由于要找到最长无重复的子串，因此一定与该字符 相同的前一个字符 的位置有关。

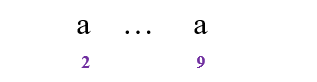
例如，假设 3 到 8 下标之间没有再出现a字符，则以 9 号下标为结尾的a字符往前延伸的距离最多只能到下标 3 处。

除了因素 1 外，也与该字符的 前一个字符 向前延伸的位置有关。

同样例子，假设下标为 9 的a字符的前一个字符是b， 6 到 7 下标之间没有再出现b字符，则以 8 号下标为结尾的b字符往前延伸的距离最多只能到下标 6 处。
进而导致了下标为 9 的a字符往前延伸的距离最多也只能到下标 6 处。

确定了影响最终答案的因素后，思路便豁然开朗了：

两个因素中结果较大的下标即为该位置所能扩充的最远距离。

需要解决能够找到前一个相同字符下标的方法；（使用map）
设置存储前一个字符 最远能够向前扩充的下标 变量。
取 1，2 中 较大的下标 即为该位置字符的答案。

代码

public static int lengthOfLongestSubstring(String s) {
    if (s == null || s.equals("")) {
        return 0;
    }
    char[] str = s.toCharArray();
    // 这里并没有直接使用 map , 与 map 功能类似
    // 该 map 数组中存放的是 该字符 上一次出现时 的 下标
    int[] map = new int[256];
    for (int i = 0; i < 256; i++) {
        map[i] = -1;
    }
    // 最新的答案（即此前最长的子串长度）
    int len = 0;
    // 前一个字符能够向前扩充的最远位置在哪
    int pre = -1;
    // 当前位置字符能够向前扩充的最远位置在哪
    int cur = 0;
    for (int i = 0; i != str.length; i++) {
        // 取两个因素中的最大值
        pre = Math.max(pre, map[str[i]]);
        // 此时能够扩充的最大距离
        cur = i - pre;
        // 更新答案
        len = Math.max(len, cur);
        // 更新最新该字符出现的位置
        map[str[i]] = i;
    }
    return len;
}