基于栅格占据概率和距离场的机器人覆盖轨迹模拟

简介

辐射场模型实现

理论基础

指数函数建模

我们使用指数函数来表示机器人在某个栅格上停留时间对覆盖概率的影响:

$$p(t)=1-e^{-\lambda t}$$

其中 $\lambda$ 是控制增长速率的参数,$t$ 是停留时间。

高斯函数建模

为了表示机器人停留位置对周围栅格的辐射效应,我们使用二维高斯函数

数学形式

1. 使用指数函数表示停留时间对覆盖概率的影响:

   设 $p(t)$ 表示机器人在某个栅格上停留时间 $t$ 对应的覆盖概率,可以使用指数函数来建模:

   $$p(t)=1-e^{-\lambda t}$$

   其中 $\lambda$ 是一个控制增长速率的参数。当 $t$ 较小时,覆盖概率增长较快;当 $t$ 较大时,覆盖概率增长变缓,最终趋于1。

2. 考虑周围栅格的辐射效应:

   为了表示停留时间对周围栅格的影响,可以使用二维高斯函数来建模这种"辐射"效应:

   $$G(x,y)=\frac{1}{2\pi {\sigma }^2}{e}^{-\frac{x^2+y^2}{2{\sigma }^2}}$$

   其中 $(x,y)$ 表示相对于中心栅格的坐标,$\sigma$ 控制辐射范围。

3. 结合指数函数和高斯函数:

   将指数函数和高斯函数相乘,得到综合考虑停留时间和辐射效应的覆盖概率函数:

   $$P(t,x,y)=(1-e^{-\lambda t})\cdot \frac{1}{2\pi {\sigma }^2}{e}^{-\frac{x^2+y^2}{2{\sigma }^2}}$$

   这个函数表示,对于中心栅格 $(0,0)$,覆盖概率主要由停留时间 $t$ 决定;对于周围栅格 $(x,y)$,覆盖概率同时受到停留时间 $t$ 和距离中心栅格的距离影响。

在数学上,这些方法可以称为:

1. 指数函数建模(Exponential Function Modeling):用于表示停留时间对覆盖概率的影响。

2. 二维高斯函数(2D Gaussian Function):用于表示停留时间对周围栅格的辐射效应。

3. 函数组合(Function Composition):将指数函数和高斯函数相乘,得到综合考虑停留时间和辐射效应的覆盖概率函数。

这种将多个函数组合以表示复杂现象的方法在数学建模中非常常见,可以根据具体问题选择合适的函数形式。

当然可以!下面是一个动态演示机器人在二维栅格地图上停留,并用颜色深浅表示栅格被占据情况的Python demo:

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

def exponential_coverage(t, lambda_):
    return 1 - np.exp(-lambda_ * t)

def gaussian_2d(x, y, sigma):
    return 1 / (2 * np.pi * sigma ** 2) * np.exp(-(x ** 2 + y ** 2) / (2 * sigma ** 2))

def combined_coverage(t, x, y, lambda_, sigma):
    return exponential_coverage(t, lambda_) * gaussian_2d(x, y, sigma)

# 设置参数
lambda_ = 0.1
sigma = 1.5
map_size = 30
robot_pos = (10, 14)

# 生成网格坐标
x, y = np.meshgrid(np.arange(map_size), np.arange(map_size))

# 初始化覆盖概率矩阵
coverage = np.zeros((map_size, map_size))

# 创建图形和颜色条
fig, ax = plt.subplots()
im = ax.imshow(coverage, cmap='viridis', vmin=0, vmax=1)
fig.colorbar(im)

# 更新覆盖概率矩阵的函数
def update(t):
    global coverage
    x_rel, y_rel = x - robot_pos[0], y - robot_pos[1]
    coverage += combined_coverage(1, x_rel, y_rel, lambda_, sigma)
    im.set_data(coverage)
    ax.set_title(f'Coverage at t={t}')
    return [im]

# 创建动画
ani = FuncAnimation(fig, update, frames=np.arange(0, 20), interval=500, blit=True)

plt.show()

首先定义了与之前相同的三个函数。然后,设置了模型参数 lambda_、sigma、地图大小 map_size 以及机器人的初始位置 robot_pos。

创建了一个 map_size * map_size 的网格坐标系,并初始化了一个全零的覆盖概率矩阵 coverage。使用 Matplotlib 创建图形和颜色条,并将 coverage 矩阵可视化。

update 函数用于更新覆盖概率矩阵。在每一帧中,我们计算网格坐标相对于机器人位置的偏移量,并使用 combined_coverage 函数计算每个坐标点的覆盖概率增量,将其累加到 coverage 矩阵中。然后,更新图像数据和标题。

最后,我们使用 Matplotlib 的 FuncAnimation 函数创建动画,每隔500毫秒更新一帧,共20帧。

运行这个demo,你会看到一个动态演示,显示机器人停留在 (10, 14) 位置时,周围栅格的占据情况随时间变化。颜色越深表示占据概率越高。

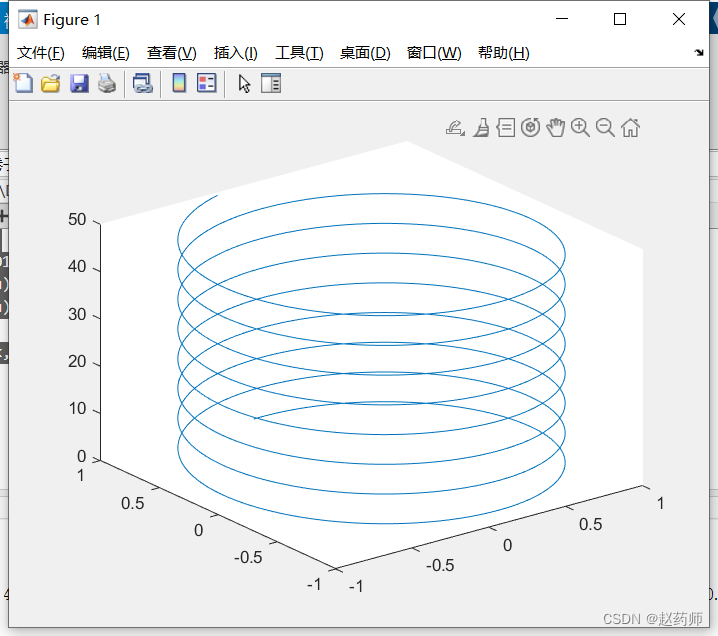
如果机器人走出一条轨迹，那就是如下图：

参考论文

1. Zelinsky, A. (1992). A mobile robot exploration algorithm. IEEE Transactions on Robotics and Automation, 8(6), 707-717.

2. Stachniss, C., & Burgard, W. (2003). Coverage of unknown environments with mobile robots using sparse models. Proceedings of the European Conference on Mobile Robots (ECMR), 1-8.

3. Solanas, A., & Garcia, M. A. (2004). Coordinated multi-robot exploration through unsupervised clustering of unknown space. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 717-721.