深度网络及经典网络简介
- 导语
- 加深网络
- 一个更深的CNN
- 提高识别精度
- Data Augmentation
- 层的加深
- 经典网络
- VGG
- GoogLeNet
- ResNet
- 高速学习
- 迁移学习
- GPU
- 分布式学习
- 计算位缩减
- 强化学习
- 总结
- 参考文献
导语
深度学习简单来说,就是加深了层数的神经网络,前面已经提到,网络的层数越深,它学习到的特征就越抽象,越高级,这也是深度网络能够胜任很多工作的原因。
加深网络
书上在本章将前面的各种技术结合起来,构建了一个复杂的深层网络,以MNIST数据集的手写识别为数据集进行训练和验证。
一个更深的CNN
书上给出了一个构造好的CNN,如下图,可以发现它比先前构造的任何网络都更深,并且使用了Dropout,选取的卷积核都是3×3,激活函数采用ReLU,使用Adam最优化,以He初始值为权重初始值。

书上给出的代码如下:
class DeepConvNet:
def __init__(self, input_dim=(1, 28, 28),
conv_param_1 = {'filter_num':16, 'filter_size':3, 'pad':1, 'stride':1},
conv_param_2 = {'filter_num':16, 'filter_size':3, 'pad':1, 'stride':1},
conv_param_3 = {'filter_num':32, 'filter_size':3, 'pad':1, 'stride':1},
conv_param_4 = {'filter_num':32, 'filter_size':3, 'pad':2, 'stride':1},
conv_param_5 = {'filter_num':64, 'filter_size':3, 'pad':1, 'stride':1},
conv_param_6 = {'filter_num':64, 'filter_size':3, 'pad':1, 'stride':1},
hidden_size=50, output_size=10):
#输入维度,卷积层数量,卷积层规模,填充,步长
pre_node_nums = np.array([1*3*3, 16*3*3, 16*3*3, 32*3*3, 32*3*3, 64*3*3, 64*4*4, hidden_size])
wight_init_scales = np.sqrt(2.0 / pre_node_nums) # 使用ReLU的情况下推荐的初始值
self.params = {}
pre_channel_num = input_dim[0]
for idx, conv_param in enumerate([conv_param_1, conv_param_2, conv_param_3, conv_param_4, conv_param_5, conv_param_6]):
self.params['W' + str(idx+1)] = wight_init_scales[idx] * np.random.randn(conv_param['filter_num'], pre_channel_num, conv_param['filter_size'], conv_param['filter_size'])
self.params['b' + str(idx+1)] = np.zeros(conv_param['filter_num'])
pre_channel_num = conv_param['filter_num']
self.params['W7'] = wight_init_scales[6] * np.random.randn(64*4*4, hidden_size)
self.params['b7'] = np.zeros(hidden_size)
self.params['W8'] = wight_init_scales[7] * np.random.randn(hidden_size, output_size)
self.params['b8'] = np.zeros(output_size)
# 生成层===========
self.layers = []
self.layers.append(Convolution(self.params['W1'], self.params['b1'],
conv_param_1['stride'], conv_param_1['pad']))
self.layers.append(Relu())
self.layers.append(Convolution(self.params['W2'], self.params['b2'],
conv_param_2['stride'], conv_param_2['pad']))
self.layers.append(Relu())
self.layers.append(Pooling(pool_h=2, pool_w=2, stride=2))
self.layers.append(Convolution(self.params['W3'], self.params['b3'],
conv_param_3['stride'], conv_param_3['pad']))
self.layers.append(Relu())
self.layers.append(Convolution(self.params['W4'], self.params['b4'],
conv_param_4['stride'], conv_param_4['pad']))
self.layers.append(Relu())
self.layers.append(Pooling(pool_h=2, pool_w=2, stride=2))
self.layers.append(Convolution(self.params['W5'], self.params['b5'],
conv_param_5['stride'], conv_param_5['pad']))
self.layers.append(Relu())
self.layers.append(Convolution(self.params['W6'], self.params['b6'],
conv_param_6['stride'], conv_param_6['pad']))
self.layers.append(Relu())
self.layers.append(Pooling(pool_h=2, pool_w=2, stride=2))
self.layers.append(Affine(self.params['W7'], self.params['b7']))
self.layers.append(Relu())
self.layers.append(Dropout(0.5))
self.layers.append(Affine(self.params['W8'], self.params['b8']))
self.layers.append(Dropout(0.5))
self.last_layer = SoftmaxWithLoss()
def predict(self, x, train_flg=False):#预测
for layer in self.layers:
if isinstance(layer, Dropout):
x = layer.forward(x, train_flg)
else:
x = layer.forward(x)
return x
def loss(self, x, t):#计算损失
y = self.predict(x, train_flg=True)
return self.last_layer.forward(y, t)
def accuracy(self, x, t, batch_size=100):#返回准确度
if t.ndim != 1 : t = np.argmax(t, axis=1)
acc = 0.0
for i in range(int(x.shape[0] / batch_size)):
tx = x[i*batch_size:(i+1)*batch_size]
tt = t[i*batch_size:(i+1)*batch_size]
y = self.predict(tx, train_flg=False)
y = np.argmax(y, axis=1)
acc += np.sum(y == tt)
return acc / x.shape[0]
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.last_layer.backward(dout)
tmp_layers = self.layers.copy()
tmp_layers.reverse()
for layer in tmp_layers:
dout = layer.backward(dout)
# 设定
grads = {}
for i, layer_idx in enumerate((0, 2, 5, 7, 10, 12, 15, 18)):
grads['W' + str(i+1)] = self.layers[layer_idx].dW
grads['b' + str(i+1)] = self.layers[layer_idx].db
return grads
训练和测试的结果如下:

提高识别精度
提高识别精度,无非是几个思路:从数据下手,获取更多的有效数据,如数据扩充,从结构下手,加深网络或采取优化算法,如学习率衰减,从学习方法下手,如集成学习等。
Data Augmentation
数据扩充很好理解,对于有限的输入数据,我们可以人为地拓展出更多的数据,例如旋转、平移、放大、缩小还有翻转等等,甚至是调整对比度、亮度,这样就可以增加许多的训练数据,在Yolov5中,数据在输入时就会被拼接翻转,形成新的数据供以训练。
层的加深
一般来说,层次越深,深度网络的识别性能就越高,并且,加深层与没有加深的网络比,可以用更少的参数达到同等水平或更强的效果。
可以这样理解,一个大卷积核可以通过多个小卷积核进行串联操作实现相同效果,一个5×5的卷积核需要25个参数,而5×5的卷积核也可以通过两个3×3的卷积核连续卷积两次得到,需要18个参数,并且,叠加小卷积核可以扩大感受野(给神经元施加变化的某个局部空间区域)。
加深层也可以使学习更高效,减少学习数据,在学习过程中可以将问题分层次的分解,就像前面所提到的,先关注边缘,再关注纹理,再关注更高级的信息。
经典网络
很多经典的深度学习网络,都基于了CNN的思想和设计模式,下面简单介绍几个。
VGG
VGG是经典的由卷积层和池化层构成的CNN,它将卷积层和池化层叠加到了16或者19层,使用的是3×3卷积核,结构如下图:
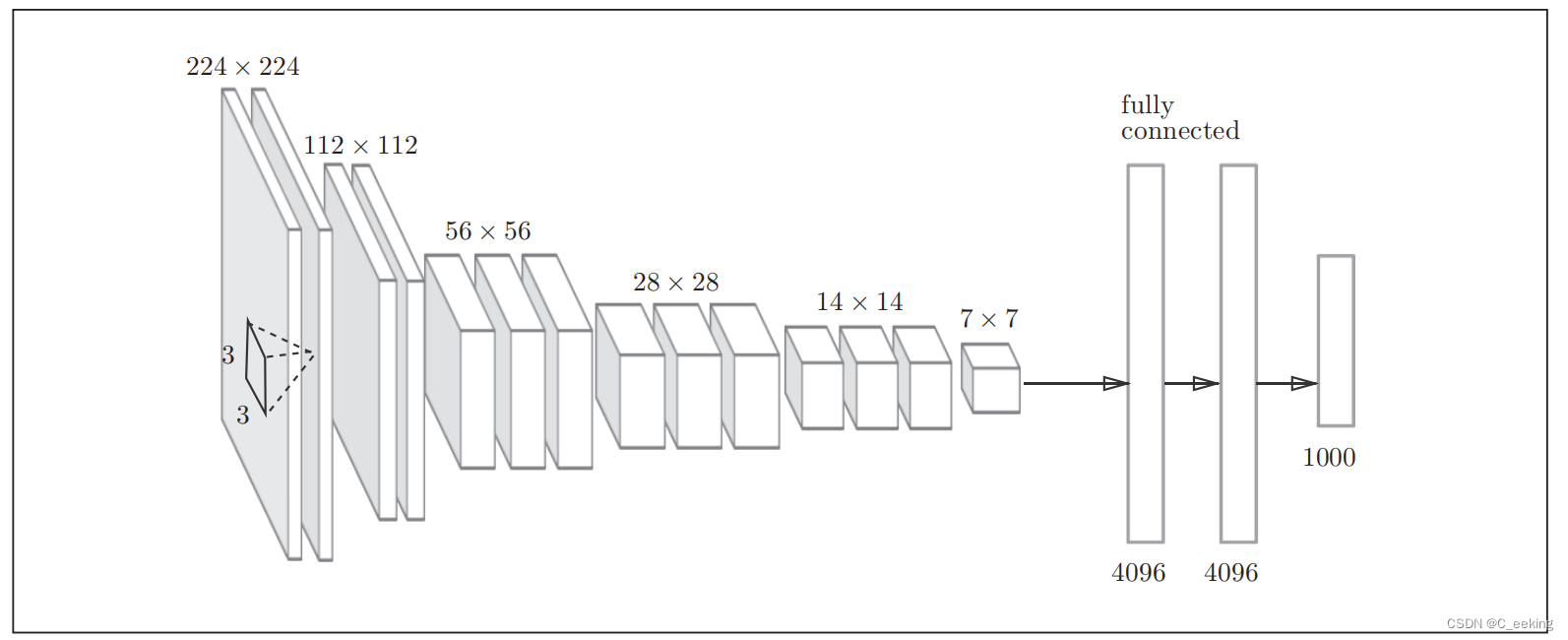
GoogLeNet
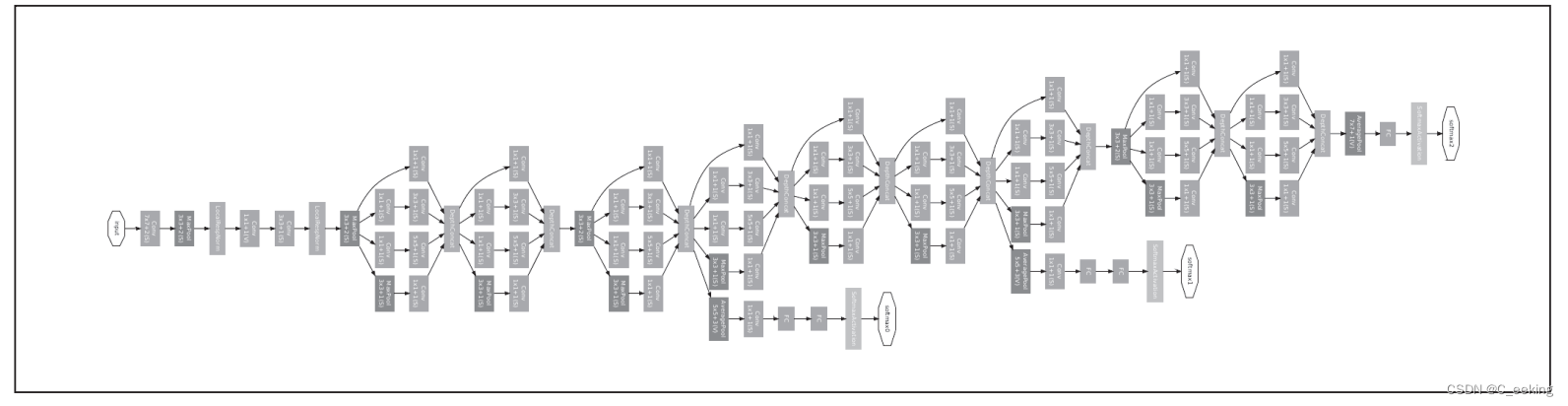
GoogLeNet在纵向上有深度,在横向上有点深度,它打破了传统的线性结构,将神经网络的结构拓展到了二维,这种宽度结构被称为Inception。
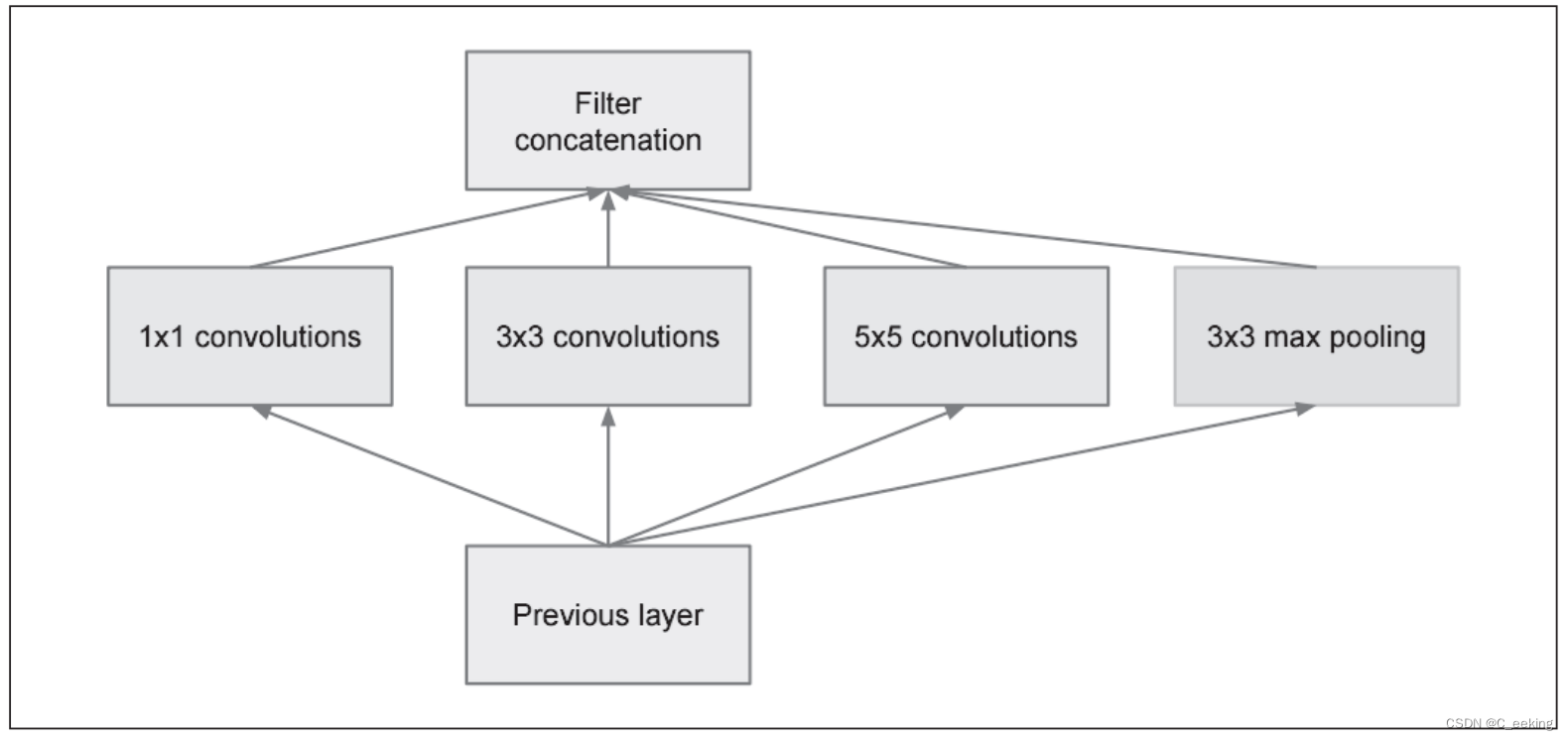
Inception使用多个大小不同的卷积核进行操作,最后将结果汇总,有点类似Dropout的思想,但是这里变的是卷积核,而不是神经元。
网络结构和Inception如下图:
ResNet
ResNet比它的前辈有着更深的结构,它考虑到,虽然加深层理论上会提高性能,但也会加大训练难度,因此使用了快捷结构,如下图:
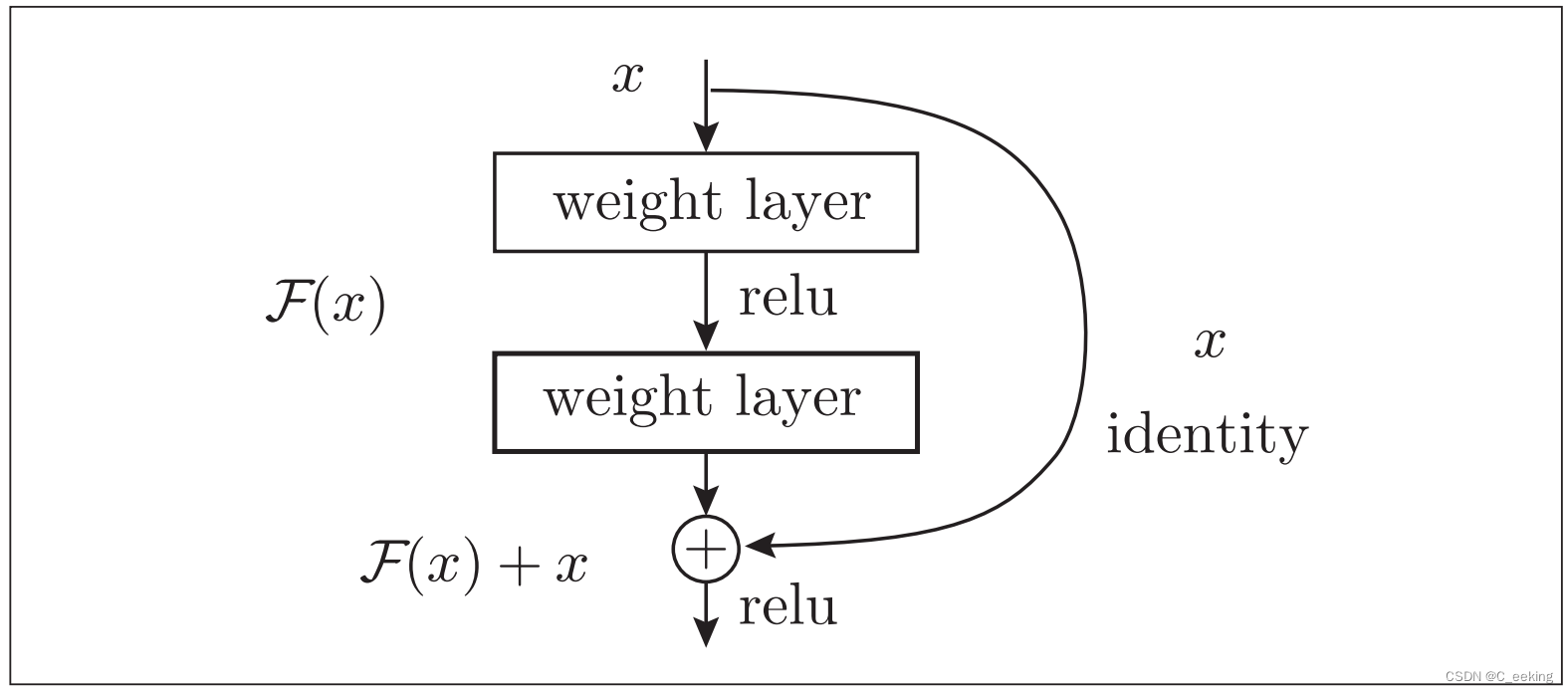
快捷结构跳过了卷积层,将输入合并到了输出,反向传播时信号可以无衰减的传递。
ResNet网络结构如下图:

高速学习
深度网络的结构和层次越来越复杂,为了更快的得到训练模型,这就需要减少学习的实现以提高效率。
迁移学习
在深度学习中,经常将ImageNet学习到的权重(或一部分)赋值给其他的深度网络,以新数据集作为对象进行再学习,这在数据集较少时很有效。
GPU
CPU虽然常用,但它并不是深度学习进行训练的最好选择,因为它并不擅长运算,相比之下GPU更适合进行深度学习的训练,以Yolov8为例,使用GPU训练5000张图片时,需要7到8个小时,而使用CPU则需要三天,GPU擅长大量的并行计算,CPU擅长连续的复杂计算。
分布式学习
虽然GPU可以减少单次训练的时间,但是深度学习的很多超参数需要不停的尝试,加起来的总时间依然不乐观,于是分布式学习应运而生(将深度学习过程拓展开来)。
分布式学习在多个GPU或机器上进行分布式运算,现在的大多数深度学习框架都集成了这一点(如TensorFlow)。
计算位缩减
常用的数据长度为64位和32位,但深度学习其实并需要这么高的精度,因为只要数据的偏差在允许的范围内,都不会影响最后的结果,这是神经网络的健壮性,根据以往结果,为了提高效率,可以使用16位的浮点数进行运算。
强化学习
强化学习针对的对象是计算机,让计算机进行自主学习。强化学习的基本逻辑是,代理根据环境选择行动,然后通过行动改变环境,两者相互影响和交互,根据环境变化,代理会受到反馈,如图:
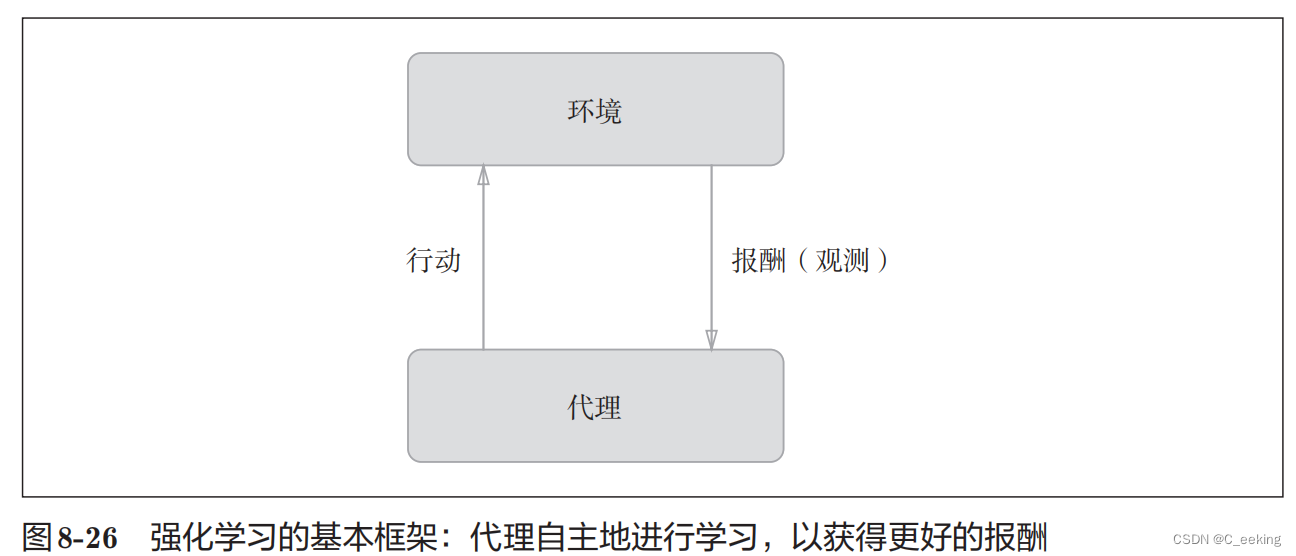
报酬是不确定的,只是有一个预测值。在使用了深度学习的强化学习方法里面,DQN很有名,它为了确定最合适的行动,需要确定一个被称为最优行动价值函数的函数,这个函数是通过深度学习得到的,大名鼎鼎的AlphaGo也是基于强化学习研究的。
总结
本章给出了一个复杂CNN的实现,并且介绍了许多优化方法以及经典网络,可以看到CNN的使用是非常广泛的,作为一个开创性的模型,CNN值得所有学习深度学习的人细细品味。
至此,深度学习入门的笔记已经全部结束。
参考文献
- 《深度学习入门——基于Python的理论与实现》