一、并查集的由来

考虑这样一个场景。

现有 $n$ 个元素，编号分别为 $1,2,\cdots,n$ （编号仅用来说明 $n$ 个元素互不相同）。初始时，我们给每个元素分配唯一的标识，称为 id，并规定如果两个元素的 id 相同，则它们属于同一集合。在这种定义下，初始时每个元素都单独属于一个集合。简便起见，令每个元素的 id 等于它自身的编号。

⚠️ 注意区分编号和 id 的含义，下文会经常提到这两个概念，不要混淆。

假设 $n\leq 10^5$ ，我们可以开一个 id 数组用来记录初始时每个元素所属的集合

#include <iostream>
#include <numeric>

using namespace std;

const int N = 1e5 + 10;

int id[N];

int main() {
    int n;
    cin >> n;
    iota(id + 1, id + n + 1, 1);
    for (int i = 1; i <= n; i++) cout << id[i] << ' ';  // 输出元素i所属的集合（即元素i的id）
    return 0;
}

给定元素 $i,j\;(1\leq i,j\leq n)$ ，如何判断两个元素是否属于同一集合呢？很简单，只需要 $O (1)$ 的时间：

cout << (id[i] == id[j] ? "Yes" : "No") << endl;

问题来了，如果我们想把元素 $i$ 所属的集合与元素 $j$ 所属的集合进行合并，该如何操作呢？根据 id 数组的定义，我们需要将其中一个集合中的所有元素的 id 赋值成另一个集合的 id，因此只能遍历：

for (int k = 1; k <= n; k++)
    if (id[k] == id[i] && id[k] != id[j])
        id[k] = id[j];

然而这种操作的时间复杂度将达到恐怖的 $O (n)$ ，在绝大多数情况下会TLE（例如当查询数量也为 $n$ 时，总时间复杂度为 $O(n^2)$ ）。

这个时候，并查集这种数据结构就派上用场了，它可以在近乎 $O (1)$ 的时间内完成上述两种操作。下面给出并查集的正式定义。

并查集（Union Find）也叫「不相交集合（Disjoint Set）」，顾名思义，它专门用于动态处理不相交集合的「合并」与「查询」问题。

并查集主要支持以下两种操作：

合并：合并两个元素所属集合；
查询：查询某个元素所属集合。这可以用于判断两个元素是否属于同一集合。

二、代表元法

代表元法的主要思想是：把每个集合看成一棵树（不一定是二叉树），树中的每一个节点都对应了一个元素，树的根节点称为该集合的代表元。对于树中的每个节点，我们不再存储它的 id，而是存储它父节点的编号。因此这里抛弃 id 数组，取而代之的是 parent 数组（以下简称 p 数组）。p 数组的定义是：p[i] 表示编号为 i 的节点的父节点的编号。特别地，定义根节点的父节点是其自身（即若 r 是根节点的编号，那么有 p[r] == r 成立）。

没有了 id，我们该如何区分每个集合呢？定义树的根节点的编号为整个树（集合）的 id，于是对于任一元素 x，我们可以「自底向上」追溯到根节点来判断它属于哪个集合：

while (p[x] != x) x = p[x];
cout << x << endl;  // 输出元素x所属集合的id（即根节点的编号）

2.1 初始化

本小节关心的问题是，p 数组如何初始化？

根据代表元法，最初每个元素都是一棵树，树中只有根节点，因此对于任一元素 $i$ （ $i$ 是编号），都有 $p [i] = i$ 成立。

使用 iota 函数初始化即可：

#include <iostream>
#include <numeric>

using namespace std;

const int N = 1e5 + 10;

int p[N];

int main() {
    int n;
    cin >> n;
    iota(p, p + n + 1, 0);  // 注意编号i的范围是1~n
    return 0;
}

2.2 查询

前面提到过，给定元素 x，我们可以使用如下代码来查询该元素所属集合

while (p[x] != x) x = p[x];

但是这种方法的时间复杂度为 $O (h)$ ，其中 $h$ 是树的高度。当树为链式结构时，每次查询的时间复杂度均为 $O (n)$ ，因此需要做进一步的优化。

优化方案有两种：「路径压缩」和「按秩合并」。后者的优化效果并不明显，故本文主要讲前者。

从元素 x 不断追溯到根节点会形成一条路径，如果在查询结束后，我们将该路径上的每个节点（除了根节点）都直接连接到根节点上，那么在后续的查询过程中，若查询的是该路径上的点，则时间复杂度将缩减至 $O (1)$ ，如下图所示：

路径压缩的实现十分简洁：

int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

find 函数返回元素 x 所属集合的 id，且在递归执行的过程中实现了路径压缩。这段代码的含义是，如果元素 x 不是根节点，那么就让元素 x 直接指向根节点，最后返回 x 的父节点的编号（即根节点的编号）。该函数是并查集中最为核心的部分，务必熟练掌握。

2.3 合并

合并两个集合相当于合并两棵树，我们只需要将其中一棵树的根节点指向另一棵树的根节点就可以了，如下图所示：

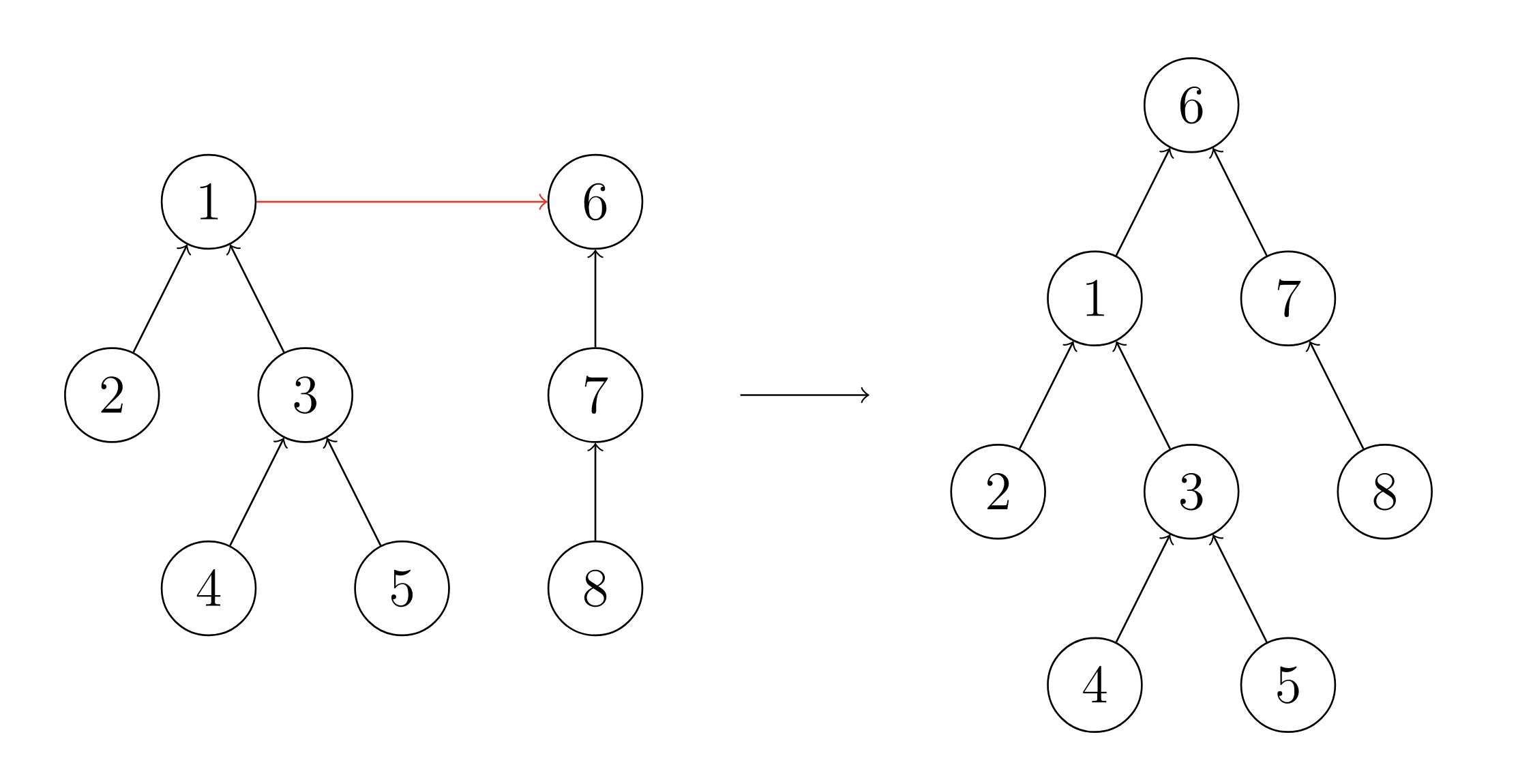
只需一行代码即可完成合并：

p[find(a)] = find(b);

2.4 设计理念

以下「三个不重要」概括了「代表元法」的设计理念：

谁作为根节点不重要：根节点与非根节点只是位置不同，并没有附加的含义；
树怎么形成的不重要：合并的时候任何一个集合的根节点指向另一个集合的根节点就可以；
树的形态不重要：理由同「谁作为根节点不重要」。

三、并查集的应用

3.1 合并集合

原题链接：AcWing 836. 合并集合

该题是并查集的模板题，思路就是本文的内容，因此不再赘述，直接给出AC代码：

#include <iostream>
#include <numeric>

using namespace std;

const int N = 1e5 + 10;

int p[N];

int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main() {
    ios::sync_with_stdio(false), cin.tie(nullptr);

    int n, m;
    cin >> n >> m;
    iota(p, p + n + 1, 0);

    while (m--) {
        char op;
        int a, b;
        cin >> op >> a >> b;
        if (op == 'M') p[find(a)] = find(b);
        else cout << (find(a) == find(b) ? "Yes" : "No") << endl;
    }

    return 0;
}

3.2 连通块中点的数量

原题链接：AcWing 837. 连通块中点的数量

不难看出，本题中的「连通块」就是集合，前两个操作我们已经见过，对于第三个操作，我们需要额外维护一个 cnt 数组，其中 cnt[i] 表示编号为 $i$ 的节点所属集合的点的数量。确切地说，我们只维护每个集合中根节点的 cnt，即只保证根节点的 cnt 是有意义的。

对于操作 Q1，只需判断 find(a) == find(b) 是否成立即可。

对于操作 Q2，因为只保证了根节点的 cnt 是有意义的，所以输出 cnt[find(a)] 而不是 cnt[a]。

对于操作 C，在合并元素 a 和元素 b 所属集合时，cnt 数组也需要更新。将 a 所属集合的根节点指向 b 所属集合的根节点的操作为：p[find(a)] = find(b)，此时 b 所属集合的大小要加上 a 所属集合的大小：cnt[find(b)] += cnt[find(a)]。需要注意的是，cnt 数组更新必须发生在集合合并之前，此外，如果 a 和 b 属于同一集合，则什么也不用做。

AC代码：

#include <iostream>
#include <numeric>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10;

int p[N], cnt[N];

int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main() {
    ios::sync_with_stdio(false), cin.tie(nullptr);

    int n, m;
    cin >> n >> m;
    iota(p, p + n + 1, 0);
    fill(cnt, cnt + n + 1, 1);  // 最初每个集合只有一个点

    while (m--) {
        string op;
        int a, b;
        cin >> op;
        if (op == "C") {
            cin >> a >> b;
            if (find(a) != find(b)) {
                // 以下两句的顺序不能调换
                cnt[find(b)] += cnt[find(a)];
                p[find(a)] = find(b);
            }
        } else if (op == "Q1") {
            cin >> a >> b;
            cout << (find(a) == find(b) ? "Yes" : "No") << endl;
        } else {
            cin >> a;
            cout << cnt[find(a)] << endl;
        }
    }

    return 0;
}

3.3 亲戚

原题链接：洛谷 P1551 亲戚

建立亲戚关系的过程相当于集合的合并，本题比较简单，直接给出AC代码：

#include <iostream>
#include <numeric>

using namespace std;

const int N = 5e3 + 10;

int p[N];

int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main() {
    ios::sync_with_stdio(false), cin.tie(nullptr);

    int n, m, q, a, b;
    cin >> n >> m >> q;  // 注意将原问题中的p改成q，防止与数组p冲突
    iota(p, p + n + 1, 0);

    while (m--) {
        cin >> a >> b;
        p[find(a)] = find(b);
    }

    while (q--) {
        cin >> a >> b;
        cout << (find(a) == find(b) ? "Yes" : "No") << endl;
    }

    return 0;
}

3.4 省份数量

原题链接：LeetCode 547. 省份数量

根据题意可知， $n$ 个城市的编号分别为 $0,1,\cdots,n-1$ 。如果 isConnected[i][j] = 1 则说明第 $i$ 个城市和第 $j$ 个城市属于同一集合，此时应当合并。又注意到 isConnected 一定是一个对称矩阵，因此只需要遍历上三角部分即可。

合并结束后，我们会得到一棵棵树（一个个省份），于是省份的数量就等于树的数量等于根节点的数量。

class Solution {
public:
    int p[200];

    int find(int x) {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    int findCircleNum(vector<vector<int>> &isConnected) {
        int n = isConnected.size();
        iota(p, p + n, 0);
        for (int i = 0; i < n; i++)
            for (int j = i + 1; j < n; j++)
                if (isConnected[i][j] == 1) p[find(i)] = find(j);
        int cnt = 0;
        for (int i = 0; i < n; i++)
            if (p[i] == i) cnt++;
        return cnt;
    }
};

References

[1] https://leetcode.cn/leetbook/read/disjoint-set/oviefi/
[2] https://oi-wiki.org/ds/dsu/
[3] https://www.acwing.com/activity/content/punch_the_clock/11/