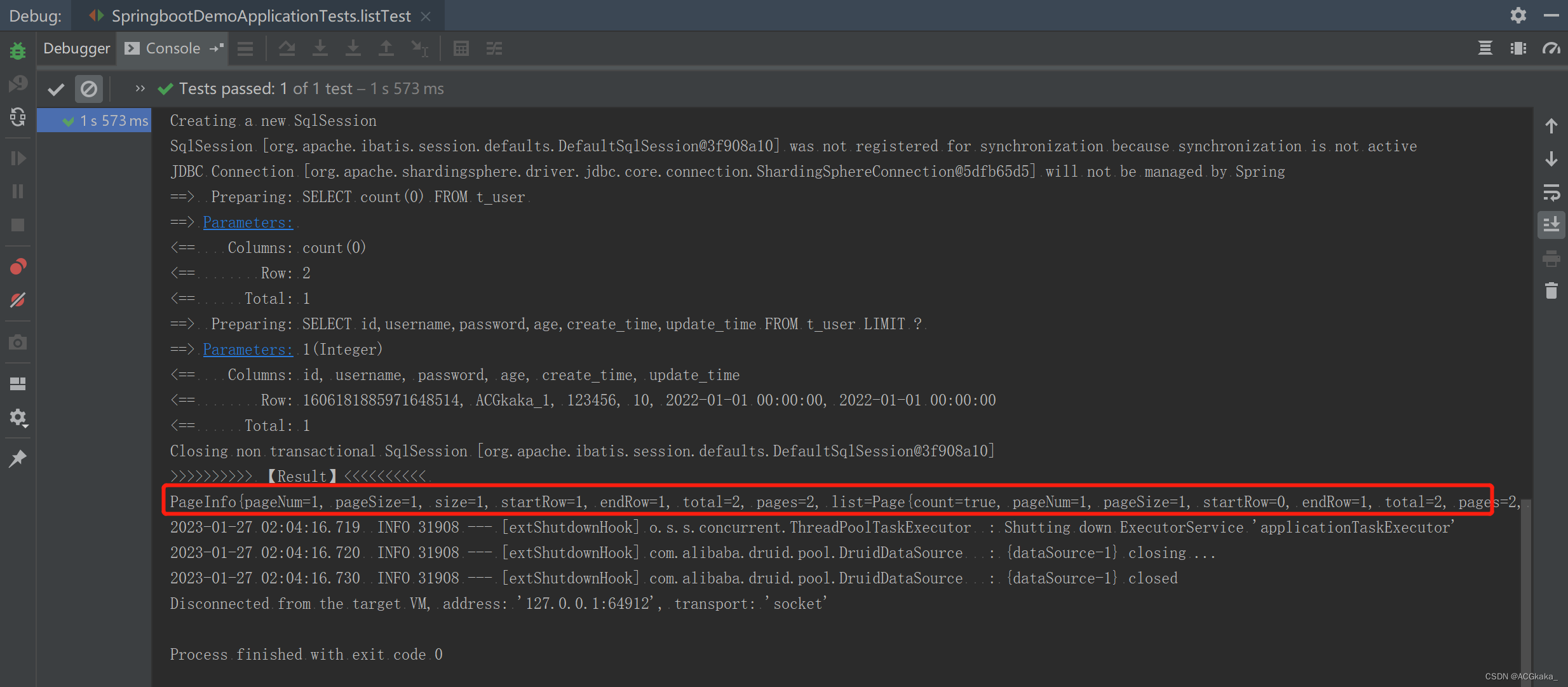
一、概念
1.1定义
应用场景：
1、最佳方案选取
2、评价类问题
3、指标体系的优选
步骤：
1、建立层次结构模型；
2、构造判断(成对比较)矩阵；
3、层次单排序及其一致性检验；
4、层次总排序及其一致性检验；
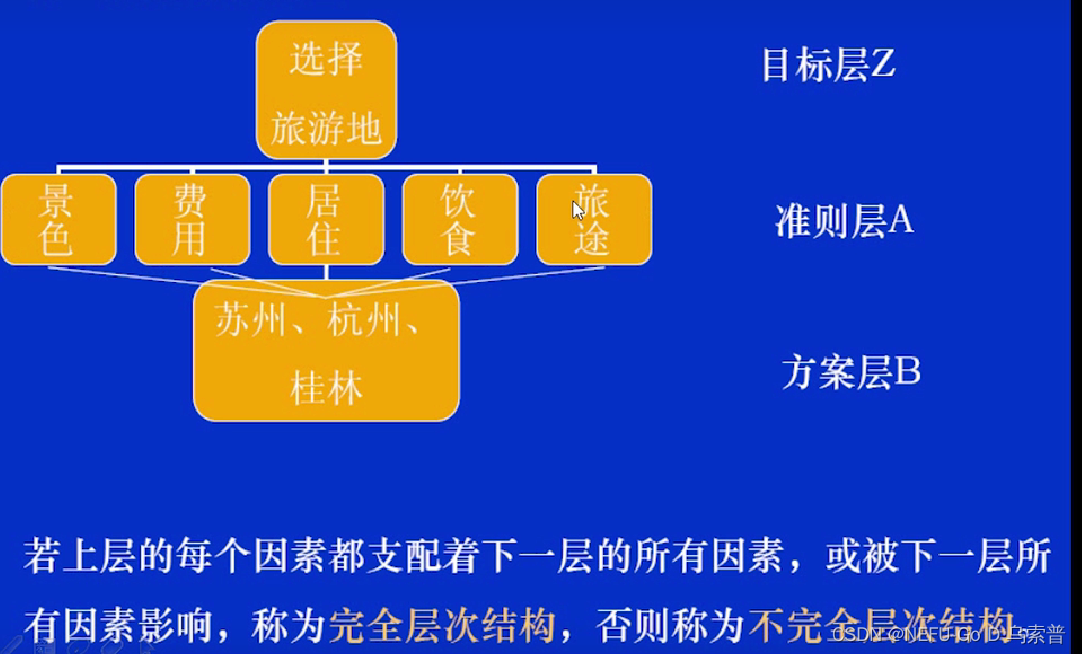
建立层次结构模型：
最高层(目标层)：决策的目的、要解决的问题；
中间层(准则层或指标层)：考虑的因素、决策的准则；
最低层(方案层)：决策时的备选方案
注意：在层次划分及因素选取时，我们要注意三点:
(1). 上层对下层有支配作用;
(2)同一.层因素不存在支配关系(相互独立) ;
(3)每层因素一般不要超过9个。
构造判断矩阵
注：采用两两比较，采用1-9标度方法
很显然，这是对称矩阵
层次单排序及一致性检验：
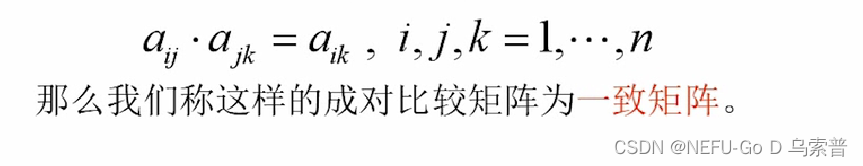
一致阵的性质：（转自知乎）
1、对称矩阵，主对角线都为1；
2、其转置也是一致阵；
3、各行成比例，则矩阵秩为1；
4、A的最大特征根(值)为 n，其余的n-1个特征根均等于0；
5、A的任一列(行)都是对应于特征根n的特征向量，AW=nW；
（这一块比较难懂，但不影响使用）
有点迷糊上例题
MATLAB实现
使用方法
（1）构造判断矩阵A
（2）将下文代码复制粘贴到Matlab中即可
例如：A=[1 3 5;0.33 1 3;0.2 0.33,1]
disp('请输入准则层判断矩阵A(n阶)');
A=input('A=');
[n,n]=size(A);
[V,D]=eig(A);%求得特征向量和特征值
%求出最大特征值和它所对应的特征向量
tempNum=D(1,1);
pos=1;
for h=1:n
if D(h,h)>tempNum
tempNum=D(h,h);
pos=h;
end
end
w=abs(V(:,pos));
w=w/sum(w);
t=D(pos,pos);
disp('准则层特征向量w=');disp(w);disp('准则层最大特征根t=');disp(t);
%以下是一致性检验
CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59 1.60 1.61 1.615 1.62 1.63];
CR=CI/RI(n);
if CR<0.10
disp('此矩阵的一致性可以接受!');
disp('CI=');disp(CI);
disp('CR=');disp(CR);
else disp('此矩阵的一致性验证失败，请重新进行评分!');
end
python实现
w=np.linalg.eig(a) #np.linalg.eig(matri)返回特征值和特征向量
t=np.argwhere(w[0]==a_max) #寻找最大特征值所在的行和列
import numpy as np
#计算特征向量和最大特征值
a=np.array([[1,1/2,1/5],[2,1,1/2],[5,2,1]]) #建立一个二维数组
w=np.linalg.eig(a) #np.linalg.eig(matri)返回特征值和特征向量
a_max=np.max(w[0])
t=np.argwhere(w[0]==a_max) #寻找最大特征值所在的行和列
RILIST=[0,0,0,0.52,0.89,1.12,1.26,1.36,1.41,1.46,1.49,1.52,1.54,1.56,1.58,1.59]
n=a.shape[0]
RI=RILIST[n]
CI=(a_max-n)/(n-1)
CR=CI/RI
print(CR)
print("矩阵一致性可接受") if CR<0.1 else print("矩阵一致性不可接受")
ans=w[1][::-1,t[0]]
SUM=sum(ans)
for i in range(ans.shape[0]):
ans[i]/=SUM
为了结果的稳健性，我们也常常使用算术平均值法和几何平均值法求权重
'''
算术平均值法
'''
import numpy as np
a=np.array([[1,1/2,1/4],[2,1,1/2],[4,2,1]])
b=np.sum(a,axis=1)
for i in range(a.shape[0]):
for j in range(a.shape[1]):
a[j][i]/=b [j]
print(np.average(a,axis=0))
'''
几何平均值法
'''
import numpy as np
a=np.array([[1,1/2,1/4],[2,1,1/2],[4,2,1]])
b=np.power(np.prod(a,axis=0),1/a.shape[0]) #累乘
b=b/np.sum(b)
print(b)
