0、背景技术概述
永磁直流电机(PMDC)、永磁同步电机(PMSM)、无刷直流电机(BLDC)以及混合式两相步进电机在小功率应用场景中多采用集成芯片驱动(如二合一、三合一驱动芯片)的原因主要包括以下几个方面:
小型化与高集成度:
- 小功率电机应用往往对体积、重量和空间布局有较高要求。集成芯片驱动将控制电路(如驱动器、控制器、保护电路等)高度集成在一个小型封装中,大大减少了外部元器件数量和电路板面积,有利于实现电机驱动系统的紧凑设计和轻量化。
简化设计与降低成本:
- 集成芯片驱动集成了电机控制所需的大部分功能,如PWM生成、电流采样、过流保护、故障检测等,省去了设计人员自行搭建复杂驱动电路的繁琐过程,降低了设计难度和工程成本。同时,批量生产的集成芯片相比分立元件具有更好的成本效益,有助于降低整体系统成本。
高效率与良好性能:
- 集成芯片通常采用优化的电路设计和先进的工艺制造,具有较低的内部损耗和较高的工作频率,能够提供高效的电机驱动能力。此外,集成芯片通常包含高级控制算法(如FOC、PID等),能够实现精确的速度控制、位置控制或转矩控制,提高电机的整体性能和动态响应。
易于使用与快速开发:
- 集成芯片驱动通常提供标准化的接口(如UART、SPI、GPIO等)和丰富的配置选项,便于与微控制器或主控系统进行通信和参数设置。开发人员只需按照芯片手册进行简单的硬件连接和软件编程,即可快速实现电机的驱动控制,大大缩短了产品研发周期。
可靠性与防护功能:
- 集成芯片内部集成了多种保护机制,如过流保护、过温保护、欠压保护等,能够在电机运行异常或外部环境恶劣时及时切断驱动信号,保护电机和驱动电路不受损坏,提高系统的整体可靠性。此外,集成芯片通常具有良好的电磁兼容性(EMC)设计,有助于满足相关法规和应用标准。
综上所述,集成芯片驱动凭借其小型化、高集成度、简化设计、高效率、易用性、良好性能以及可靠性等优势,非常适合应用于小功率电机(如永磁直流电机、永磁同步电机、无刷直流电机、混合式两相步进电机)的驱动控制,能够满足此类应用场景对空间节省、成本效益、性能优化以及快速开发的需求。二合一和三合一等集成度更高的驱动芯片进一步整合了电源管理、通信接口等功能,更加适合对体积、成本和开发周期有严格要求的小功率电机应用。
因最近需在数模混合仿真环境中进行各类电机的建模,所以先把相关的数学公式进行梳理。
以下的各个电机模型仅考虑ABC或AB坐标下的数学模型,DQ坐标系下的动态模型暂未列出。
1、无刷直流电机
无刷直流电机反电势为梯形波,定、转子互感为非正弦波,电机模型在进行 dq 轴变换时较为困难,容易引入计算误差。因此无刷直流电机更适合采用三相变量数学模型。
电机驱动系统模型做如下假设(注意前提假设条件,以下电机均涉及相关假设条件):
(1)忽略齿槽效应,定子绕组集中分布;
(2)忽略电机磁性饱和、漏感、涡流损耗和磁滞损耗;
(3)不计电枢反应,气隙磁场分布近似认为是平顶宽度为 120º 的梯形波;
(4)逆变电路中的功率器件和续流二极管具有理想开关特性。
(5)永磁体磁导率近似等同于空气磁导率,针对表面粘贴式无刷直流电机,不计转子位置变化引起的电感变化,忽略电流引起的电感饱和。电机三相绕组对称,没有电感变化,不存在转子磁阻。
无刷直流电流的反电势为梯形波,所以需要对梯形波进行建模:

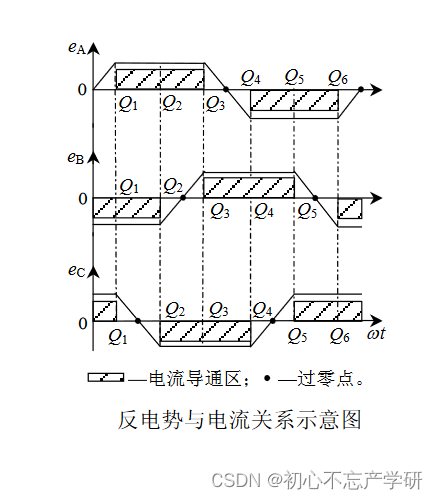
而电机电压方程可适用于常见的所有的交流电机:

运动方程同样适用于常见的所有电机:

2、永磁直流电机
永磁直流电机的数学模型较为简单,直接借用论文的公式:

3、永磁同步电机
永磁同步电机其除了反电势是正弦波之外,其他的方程与无刷直流电机一致:

4、两相步进电机
两相步进电机相当于一个单相的低速永磁同步电机,具体公式推导可参考论文:基于STM32的两相混合式步进电机闭环控制系统的研究。

5、附录
集成芯片驱动电机(尤其是那些内部集成了电机控制算法的芯片),旨在简化电机控制系统的设计,提高性能并降低成本。这类芯片通常整合了微处理器、数字信号处理器(DSP)、电源管理模块、驱动电路以及多种传感器接口,以便于直接处理复杂的电机控制算法,如磁场定向控制(FOC)。针对这些集成芯片驱动技术,其面临的技术难点主要包括以下几个方面:
高精度、实时性的算法实现:
- **FOC算法复杂度**:FOC要求精确地控制电机定子磁场与转子磁场之间的角度关系,涉及到坐标变换、电流控制、磁场估计、速度观测等多个环节。将这些算法高效且准确地在芯片内部硬件化或通过软件在微处理器上实时执行,是对芯片计算能力、内存资源和指令周期效率的挑战。
集成度与散热管理:
- **高度集成**:将多种功能模块集成到单一芯片中,需要优化布局布线、减少互连延迟,同时确保各模块间的协同工作,这对芯片设计提出了极高要求。尤其是在有限的硅片面积内集成高压驱动、低噪声模拟前端、高速数字逻辑等,需要先进的混合信号设计技术。
- **热管理**:电机驱动芯片在工作时会产生大量热量,特别是在大功率应用中。高效的散热设计、封装技术和热模型建立对于防止过热、保证长期稳定性和可靠性至关重要。如何在紧凑的空间内实现有效的散热途径是一大难点。
适应宽范围工作条件:
- **宽电压范围适应**:电机驱动芯片需能在各种电源条件下稳定工作,包括电压波动、瞬态响应等。设计需考虑宽输入电压范围的稳压电路,以及在不同电压下的效率优化。
- **动态性能与鲁棒性**:芯片应具备快速响应负载变化的能力,同时在电机参数变化(如电机阻抗随温度变化)、电机故障(如短路、断路)等异常情况下保持稳定运行,需要有强大的故障检测与保护机制。
EMC兼容性与抗干扰能力:
- **电磁兼容性(EMC)**:电机驱动环境往往存在严重的电磁干扰,集成芯片必须符合严格的EMC标准,包括辐射发射、传导发射、抗扰度测试等。这要求芯片内部具有良好的滤波、接地、屏蔽设计,以及高效的抗干扰算法。
软件与硬件协同设计:
- **硬件加速器与软件算法配合**:对于部分复杂的计算任务,可能需要专门的硬件加速器(如向量处理单元、数学协处理器等)来提高计算效率。如何设计这些加速器并与软件算法无缝对接,以充分利用硬件优势,是一个技术难点。
- **编程接口与工具链支持**:为了方便用户开发和调试电机控制系统,需要提供易于使用的编程接口、开发工具、固件库以及仿真环境。构建完整的生态系统支持也是集成芯片成功的关键因素。
标准化与定制化平衡:
- **市场适应性**:电机驱动芯片需要满足不同行业、不同应用的需求,既要遵循国际或行业标准(如汽车行业的ISO 26262功能安全标准),又要能灵活适应特定客户或市场的特殊要求。如何在标准化产品基础上提供足够的定制化选项,是芯片厂商面临的挑战。
综上所述,集成芯片驱动电机技术难点涉及算法复杂度、集成度与散热、工作条件适应性、EMC兼容性、软硬件协同设计以及标准化与定制化平衡等多个方面。解决这些难点需要芯片设计者具备深厚的电机控制理论知识、先进的集成电路设计技术以及对目标应用领域的深入理解。










![[图解]建模相关的基础知识-06](https://img-blog.csdnimg.cn/direct/01ca8a30c0c7465484781733292497e5.png)


