最小相位系统

1、传递函数

一个线性系统的响应。

比如一个RC低通滤波器：

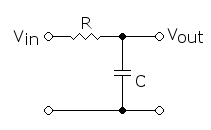
交流分量在电容的充放电中被滤除掉，通过设置电容器的电容值，以及电阻值，能够控制这种滤除能力，这个参数为RC。

电容的电抗为$1/jwC$，因此容易的写出其频率响应，其中 V i n = ∑ k = 1 L A k ℜ { exp ⁡ ( j ϕ k ) exp ⁡ ( j w t ) } V_{in} = \sum_{k=1}^{L}A_k\Re\{\exp(j\phi_k)\exp(jwt)\} Vin​=∑k=1L​Ak​ℜ{exp(jϕk​)exp(jwt)}：
$$V_{out}=\frac{1/jwC}{R+1/jwC}{V}_{in}=\frac{1}{1+jwRC}{V}_{in}$$
将这个系数提出来：
$$H(w)=\frac{1}{1+jwRC}$$
这是一个变量为角频率的复变函数。为了便于在二维空间展示，对其取模、取相角，分别得到幅频响应和相频响应。求逆傅立叶变换得到$h(t)$​，冲激函数响应。

此时的$H(w)$是一种传递函数（transfer function）。

以上是简单情况，仅当输入信号存在傅立叶变换的时候才成立，傅立叶变换要求输入信号绝对可积。对于更一般的情况，对频率进行推广。傅立叶变换的核函数是$e^{jwt}$，将纯虚数推广到复数，就能够对幅度进行调控，即$e^{st}=e^{(a+jb)t}=e^{at}{e}^{jbt}$。至于衰减还是增加，取决于$a$的正负。

得到：
$$H(s)=\frac{1}{1+sRC}$$
当s取纯虚数的时候，等于频率响应。

为了便于分析，将$H(s)$画在一个复平面上，横轴为实轴，纵轴为虚轴。

这个系统是一个因果系统，没有输入的时候不会有输出。因此其时域响应是一个右边信号，因此其收敛域为 R O C = { s ∣ ∣ s ∣ > − R C } ROC = \{s\mid |s|> -RC\} ROC={s∣∣s∣>−RC}。

包含虚轴，那么该系统稳定。有理+极点在左半平面，因此系统因果。

2、最小相位

比较相位大小，首先要保证幅频响应相同，或者说幅度增益相同，否则没有意义。

结论：系统首先要求因果+稳定

1. 拉普拉斯变换：零极点都在左半复平面
2. z变换：零极点都在单位圆内

则是最小相位系统

首先系统要求稳定，即有界输入对应有界输出，其充要条件是ROC包含虚轴。

其次系统要求因果，即$h(t)=0,\forall t<0$，暂时没有好的充要条件，但又一些有意义的结论：

1. 必要条件：ROC是某个右半复平面。（$h(t)$至少要求是右边信号，起点还不确定，所以仅仅是个必要条件）
2. 充分条件：传递函数是有理的，并且ROC为最右侧极点的右半复平面。

那么，下面的讨论中，假设传递函数可以用有理函数表示。（这意味着其时域响应可以用复指数函数表示）
$$H(s)=\frac{N(s)}{D(s)}\text{\hspace{1em}(2-1)}$$

---

接下来再说什么情况下两个系统的幅度增益是相同的。
$$|H_1(s)|=\frac{|N_1(s)|}{|D_1(s)|}=\frac{|N_2(s)|}{|D_2(s)|}=|H_2(s)|\text{\hspace{1em}(2-2)}$$
从上面公式（2-2）可以看出，幅度相同，意味着分子分母的幅度都相同。

根据有理传递函数的假设，其分子分母都可以用多项式表示，再由代数基本定理，该多项式可以写成连乘的形式。

先讨论分母，其中A是一个常数，$a_i,i=1,2,...,N$：
$$D(s)=A{\Pi }_{i=1}^N(1-a_i{s}^{-1})=A(1-a_1{s}^{-1})(1-a_2{s}^{-1})\cdots (1-a_N{s}^{-1})\text{\hspace{1em}(2-3)}$$
如果要求系统因果稳定，那么 ℜ { a i } < 0 \Re\{a_i\}<0 ℜ{ai​}<0，且ROC为右半平面。

因此必有$D_1(s)=D_2(s)$​，否则必有一个不满足因果稳定的条件。

再讨论分子，其中B是一个常数，$b_i,i=1,2,...,M$：
$$N(s)=B{\Pi }_{i=1}^M(1-b_i{s}^{-i})=B(1-b_1{s}^{-1})(1-b_2{s}^{-1})\cdots (1-b_M{s}^{-1})\text{\hspace{1em}(2-4)}$$
系统因果稳定跟分子没有关系，因此$b_i\in C$，为任意复数。

因此，两个因果稳定的系统，幅度增益相同，相位响应不同，只能从分子入手，分母不能动。

---

对任意一项$(1-b_i{s}^{-1})$，其中$s=\sigma +jw,b_i=x+jy$。取相角：
$$\begin{gathered} \varphi =\measuredangle (1-b_i{s}^{-1})=\arg (1-\frac{x+jy}{\sigma +jw})=\arg (\frac{\sigma -x+j(w-y)}{\sigma +jw})=\arg (K{e}^{{\varphi }_1-{\varphi }_2}) \\ K=\frac{\sqrt{(\sigma -x{)}^2+(w-y{)}^2}}{\sqrt{{\sigma }^2+w^2}} \\ \varphi ={\varphi }_1-{\varphi }_2=\arctan 2(\frac{w-y}{\sigma -x})-\arctan (\frac{w}{\sigma }) \end{gathered}$$

讨论相频响应，需要令$\sigma =0$，频率$w$从0开始递增，通常使用波特图来描述，横坐标用类似于np.linspace(1e-2,1e2,1000)的语句来描述。

因此${\varphi }_2=\pi /2$，${\varphi }_1=\arctan 2(\frac{w-y}{-x})$，需要注意$\arctan 2$的输出范围是$[-\pi ,\pi )$。因此当$-x>0$为常数，$w-y>0$的时候，返回的是一个一象限的锐角，因此${\varphi }_1$从$-\pi /2$递增到0。反过来将从$\pi /2$递减到0

可以用python代码来描述这个过程：

import numpy as np
import matplotlib.pylab as plt
# (1-bs^-1)
sigma = 0
Npoints = 1000
w = np.linspace(1e-1,100,Npoints)
s = sigma+1j*w

b = -5+1j*0

y1 = np.angle((1-b/s), deg=True)
y2 = np.angle((1+b.conjugate()/s), deg=True)

x1 = np.abs(1-b/s)
x2 = np.abs(1+b.conjugate()/s)
plt.semilogx(w,y1,'ro')
plt.semilogx(w,y2,'b*')
plt.legend(["negtive poles","positive poles"])
plt.show()

上述推导属实令人费解，主要原因是我们采用了负幂来描述这个系统。实际上，在控制工程当中，使用正幂来描述连续时间系统会更加常见。

如果是正幂，那么分子中的一项为$(s-b_i)$，令s的实部为0，即$s=jw$，那么
$$\begin{gathered} \measuredangle (s-b_i)=arctan2(\frac{w-y}{-x}) \\ |(s-b_i)|=\sqrt{x^2+(w-y{)}^2}\text{\hspace{1em}(2-5)} \end{gathered}$$
显然，要使得幅频响应不变，那么$b_i$的虚部不能动，实部的正负可以变。

	$(w-y)>0$	$(w-y)<0$
实部为正（位于正半平面）	正钝角	负钝角
实部为负（位于负半平面）	正锐角	负锐角

所以，当实部为负，即零点在负半平面，随着频率的变化，相位变化相比于零点在正半平面更慢。也就是说相位变化小，即群时延小，阶跃响应建立更快，冲激响应能量更向0时刻集中。需要注意，最小相位系统，其相位延迟不一定是最小，但是相位变化一定是最小。比如一个最小相位系统的相位延迟了45度，另外一个相同幅频响应的系统相位延迟可能只有30度。

总结

Tip1:

关于最小相位系统有一些等价条件：

1. 群时延最小的系统
2. 冲激响应能量最靠近0时刻的系统
3. 阶跃响应建立最快的系统
4. 有理传递函数的情况下，零极点都在复平面的左半平面的系统
5. 有理传递函数的情况下，对于离散时间系统，零极点都在单位圆内的系统
6. 有理传递函数的情况下，系统和逆系统都是因果稳定的系统

Tip2:

最大相位系统：零点都在右半平面。因此这种系统因果稳定，但是其逆系统则不可能同时因果稳定。

Tip3:

一个零极点系统可以表示成最小相位系统和全通系统的乘积。

比如：
$$H(s)=\frac{s-1}{(s+3)(s+2)}=\frac{s-1}{(s+3)(s+2)}\times \frac{s-1}{s+1}$$

$$H(z)=\frac{1-(2e^{j\pi /3})z^{-1}}{(1-3z^{-1})(5-z^{-1})}=\frac{z^{-1}-2e^{-j\pi /3}}{(z^{-1}-3)(5-z^{-1})}\times \frac{1-(2e^{j\pi /3})z^{-1}}{z^{-1}-2e^{-j\pi /3}}\times \frac{z^{-1}-3}{1-3z^{-1}}$$

Tip4:

已知幅频响应，那么其最小相位系统的相频响应响应是唯一的。