文章目录
- 题目描述
- 代码
题目描述
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
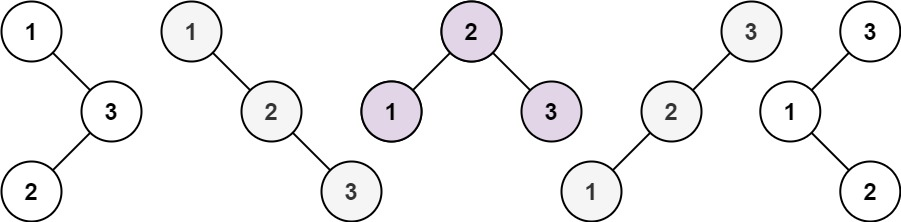
输入:n = 3
输出:5
示例 2:
输入:n = 1
输出:1
提示:
1 <= n <= 19
代码
import java.lang.annotation.Retention;
class Solution {
public int numTrees(int n) {
int[] dp = new int[n+1];
dp[0]=1;
dp[1]=1;
/*以三个点为例子,大致可以分为三种类型:
1、以1为根节点,左子树0个节点,右子树2个节点,总共两种树的形态
2、以2为根节点,左右子树各1个节点,总共1种树的形态
3、以3为根节点,左子树2个节点,右子树0个节点,总共2种树的形态
所以dp[3]也就是n=3的时候二叉搜索树的形态的个数是这三种情况之和:2+1+2
对于n=i的时候来讲,左子树有j个节点,右子树就只能有i-j-1个节点,根据数学中组合排列的内容,形态总数应该是左子树的形态数乘以右子树的形态数,即dp[j]*dp[i-j-1]
最终,n=i的时候的形态总数是选不同节点作为根节点所能够形成的树的形态个数之和,即dp[i] = dp[i]+dp[j]*dp[i-j-1];
*/
for (int i = 2; i <=n ; i++) {
for (int j = 0; j <i ; j++) {//这里选择j从0开始的意思是j代表左子树上节点的数量,左子树上最开始一个节点没有全都在右子树上
dp[i] = dp[i]+dp[j]*dp[i-j-1];
}
}
return dp[n];
}
}