一、编程题
第1题:求和
【题目描述】
输入一个正整数 N(N < 100),输出 1 到 N(包含 1 和 N)之间所有奇数的和。
【输入描述】
输入一个正整数 N(N < 100)
【输出描述】
输出 1 到 N 之间的所有奇数的和
【输入样例】
3
【输出样例】
4
答案:
参考代码一:
#include <iostream>
using namespace std;
int main() {
int n;
cin >> n;
int sum = 0;
for (int i = 1; i <= n; i++) {
if (i % 2 == 1) {
sum += i;
}
}
cout << sum << endl;
return 0;
}
参考代码二:
#include <bits/stdc++.h>
using namespace std;
int n;
int main() {
cin >> n;
int sum = 0;
for (int i = 1; i <= n; i += 2)
sum += i;
cout << sum;
return 0;
}
本题属于简单题,考察累加器和循环的使用。定义累加器 sum 并初始化为 0,循环枚举i从1到 n,判断i如果为奇数,则累加 sum+=ì。循环结束后输出 sum。对循环理解较好的同学,也可以去掉 ǐ 判断,将 i++改为i+= 2,直接累加,也可达到奇数求和的效果。
第2题:求平方
【题目描述】
平方是一种运算,比如:a 的平方表示 a × a。
例如:2 的平方为 4(也就是 2*2 的积)
例如:4 的平方为 16(也就是 4*4 的积)
输入一个正整数 N(N < 30),输出 1 到 N(包含 1 和 N)之间所有正整数的平方,且所输出的平方数之间以英文逗号隔开。
【输入描述】
输入一个正整数 N(N < 30)
【输出描述】
输出所有正整数的平方数,以英文逗号隔开
【输入样例】
3
【输出样例】
1,4,9
答案:
参考代码一:
#include <iostream>
using namespace std;
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; i++) {
cout << i * i;
if (i != n) {
cout << ",";
}
}
return 0;
}
参考代码二:
#include <bits/stdc++.h>
using namespace std;
int n;
int main() {
cin >> n;
cout << "1";
for (int i = 2; i <= n; i++)
cout << ',' << i * i;
return 0;
}
本题属于简单题,考察循环的使用。大部分失分的同学主要错在输出格式上。题目中要求输出时用英文逗号隔开,不能加空格或者使用中文逗号,并且最后一个平方数后面不能有英文逗号,因此在循环输出时,判断循环变量i,如果不是输出最后一个数,则输出英文逗号””,否则不输出。
第3题:数位递增数
【题目描述】
一个正整数如果任何一个数位小于等于右边相邻的数位,则称为一个数位递增数。
例如:
1135 是一个数位递增数
1024 不是一个数位递增数
输入一个正整数 n(11<n<10001),输出 11 到 n(包含11和n)中有多少个数位递增数。
例如:输入 15,11 到 15 之间的数位递增数有:11、12、13、14、15。一共有 5 个。
【输入描述】
输入一个正整数 n(11<n<10001)
【输出描述】
输出 11 到 n 中有多少个数位递增数
【输入样例】
15
【输出样例】
5
答案:
参考代码一:
#include <iostream>
using namespace std;
int main() {
int n;
cin >> n;
int cnt = 0;
for (int i = 11; i <= n; i++) {
int a = i / 10000 % 10; // 万位
int b = i / 1000 % 10; // 千位
int c = i / 100 % 10; // 百位
int d = i / 10 % 10; // 十位
int e = i % 10; // 个位
if (a <= b && b <= c && c <= d && d <= e) {
cnt++;
}
}
cout << cnt << endl;
return 0;
}
参考代码二:
#include <bits/stdc++.h>
using namespace std;
int n;
int main() {
cin >> n;
int sum = 0;
for (int i = 11; i <= n; i++) {
string s;
stringstream ss;
ss << i;
ss >> s;
int f = 0;
for (int j = 1; j <= s.size() - 1; j++)
if (s[j] < s[j - 1]) {
f = 1;
break;
}
if (!f)
sum++;
}
cout << sum;
return 0;
}
本题与之前课上所做的水仙花数、四叶玫瑰数类似,考察循环枚举与数位分离的技巧。
题目中的数据范围为 11~10001,即最少为2位,最多为5位。由题意可知,一个数位递增数,在高位补0后,不会改变数的大小且仍为数位递增数。不妨在高位补 0,将所有的数当做五位数处理。例如,11、12 是数位递增数,处理时看做 00011、00012,仍为数位递增数。补齐五位后,使用数位分离的技巧,依次取出万位 a、千位 b、百位 c、十位 d、个位 e,判断是否高位数字<= 低位数字,如果是数位递增数,则计数器 cnt++,循环结束后输出 cnt,程序结束.
第4题:最短距离
【题目描述】
有一个居民小区的楼房全是一样的,并且按矩阵样式排列。其楼房的编号为 1,2,3……,当排满一行时,从下一行相邻的楼往反方向排号。
例如:小区为 3 行 6 列,矩阵排列方式:
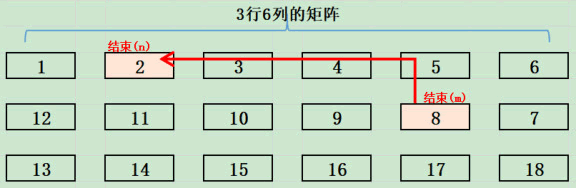
要求:已知小区楼房有 w 列及两个楼房楼号 m 和 n,求从 m 号楼到 n 号楼之间的最短路线经过几个楼(不能斜线方向移动)。
例如上图:当 w=6,m=8,n=2,从 8 号楼到 2 号楼最短的路线经过 5,4,3,2 四个楼(9,10,11,2 也经过四个楼),故最短路线为 4(注:不考虑路线只考虑最短路线经过几个楼)。
输入三个正整数 w(1<w<21),m(1<m<10001),n(1<n<10001),且 m 不等于n。三个正整数之间以一个空格隔开,输出m 到n的最短路线经过几个楼。
【输入描述】
在一行输入三个正整数 w,m,n,三个正整数之间以一个空格隔开
【输出描述】
输出 m 到 n 的最短路线经过几个楼
【输入样例】
6 8 2
【输出样例】
4
答案:
参考代码一:
#include <cmath>
#include <iostream>
using namespace std;
int main() {
int w, m, n;
cin >> w >> m >> n;
int x1, y1, x2, y2;
x1 = (m - 1) / w + 1;
y1 = (m - 1) % w + 1;
if (x1 % 2 == 0) {
y1 = w + 1 - y1;
}
x2 = (n - 1) / w + 1;
y2 = (n - 1) % w + 1;
if (x2 % 2 == 0) {
y2 = w + 1 - y2;
}
int ans = abs(x1 - x2) + abs(y1 - y2);
cout << ans << endl;
return 0;
}
参考代码二:
#include <bits/stdc++.h>
using namespace std;
int n, m, w, a[1011][1011], s1, t1, s2, t2;
int main() {
cin >> w >> n >> m;
int x = 1, y = 1, f = 0;
if (n > m)
swap(n, m);
for (int i = 1; i <= m; i++) {
a[x][y] = i;
if (i == n)
s1 = x, t1 = y;
if (i == m)
s2 = x, t2 = y;
if (f == 0)
y++;
else
y--;
if (y > w) {
x++;
y = w;
f = 1;
}
if (y < 1) {
x++;
y = 1;
f = 0;
}
}
cout << abs(s2 - s1) + abs(t2 - t1);
return 0;
}
本题重点考察题目分析和理解。我们需要计算出 m、n 号楼在第几行第几列,行、列的差相加,得到最终的结果。
例如,w=6,m=8,n=2,可以算得8号楼所在行x1=(m-1)/w+1=(8-1)16+1=2,2号楼所在行x2=(n-1)/w+1=(2-1)16+1=1:
所在列的情况比较复杂,涉及反向的问题,其中奇数行的列号从左往右依次增大,偶数行的列号从左往右依次减小,我们可以先按照从左往右依次增大的情况,算出y1=(m-1)%w+1=(8-1)%6+1=2,y2=(n-1)%w+1=(2-1)%6+1=2:
其中,2号楼在奇数行,y2=2即为所在列,8号楼在偶数行,方向相反,y1=w+1-y1=6+1-2=5,8号楼在第5列。
经过的楼数为 abs(x1-x2)+abs(y1-y2)=abs(2-1)+ abs(5-2)= 4.
将如上过程编写为程序,输出即可。
第5题:组合
【题目描述】
输入两个正整数 n 和 m(20 >= m >= n > 0),n 代表正整数的个数,要求 n 个正整数相加的和为 m,输出满足这个条件的正整数组合有多少。
例如:当 n=4,m=8 时,满足条件的有 5 组(也就是:5+1+1+1=8,4+2+1+1=8,3+3+1+1=8,3+2+2+1=8,2+2+2+2=8,每组组合都由 4 个正整数组成且 4 个正整数的和等于 8)
【输入描述】
分行输入 n 和 m(20>=m>=n>0)
【输出描述】
输出满足这个条件的正整数组合有多少
【输入样例】
4
8
【输出样例】
5
答案:
参考代码一:
#include <iostream>
using namespace std;
int n, m, sum = 0, ans = 0;
int a[25];
void dfs(int p) {
if (p > n) {
if (sum == m) {
ans++;
}
return;
}
for (int i = a[p - 1]; i <= m - sum; i++) {
sum += i;
a[p] = i;
dfs(p + 1);
sum -= i;
a[p] = 0;
}
}
int main() {
cin >> n >> m;
a[0] = 1;
dfs(1);
cout << ans << endl;
return 0;
}
参考代码二:
#include <bits/stdc++.h>
using namespace std;
int n, m, a[110], ans;
void dfs(int dps, int sum) {
if (sum > m)
return;
if (dps > n) {
if (sum == m)
ans++;
} else {
for (int i = 1; i <= m; i++) {
if (i >= a[dps - 1]) {
a[dps] = i;
dfs(dps + 1, sum + i);
a[dps] = 0;
}
}
}
return;
}
int main() {
cin >> n >> m;
dfs(1, 0);
cout << ans;
return 0;
}
做法1使用递归回溯法,设数组 a[25],a[p] 表示式子中的第 p 个加数。
设初始值 a[0]= 1,依次递归枚举 a[1]~ a[n],为了避免重复枚举,a[p]的枚举范围为 a[p-1]~(m- sum)。
计算 a[1] ~ a[n] 总和 sum,如果 sum == m,则个数 ans++。
递归结束,输出符合条件的个数 ans。