目录
一、理论
概念:
线性可分:
支持向量:
间隔:
目标:
软间隔:
梯度下降法:
别的方法:
拉格朗日函数:
SMO算法:
核函数:
二、代码
说明:
三、结果:
优缺点分析:
遇到的问题:
一、理论
svm的目的是找到一个最优的划分超平面或者决策边界,从而实现对数据的有效分割或者拟合。
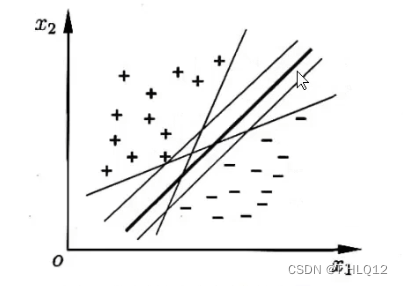
超平面:
在二维情况下,上图的线就是超平面,而若特征有3维,则超平面就是一个平面,而高维情况很多,就统一叫作超平面。
所以当有了一个数据集后,主要的问题就是如何找出这个最优的超平面。
概念:
线性可分:
现在先假设一个数据集是线性可分的。
因为超平面都可以用一个线性方程表示,其中:w是超平面的法向量。x是数据点的特征向量。b是偏置。
有了这个概念,线性可分就可以定义为:
当标签为正类(y=1)时,,
当标签为负类(y=-1)时,。
将这两个式子合起来,简写为:,使得式子统一。
支持向量:
由数学知识得到,假设一个平面为Ax+By+Cz+D=0, 那么将这个平面乘以一个数后,平面还是同一个平面,所以可以通过控制乘的这个数,使得,化简一下变为:
。
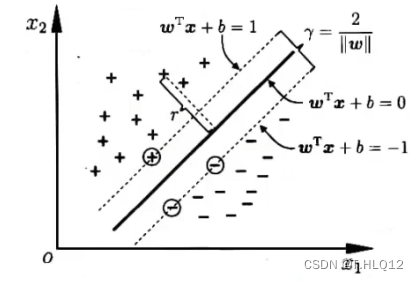
通过这样的缩放变换,当一个样本点使得,这个样本点就是距离这个超平面最近的点,我们把这些点称作支持向量。
虚线上的点就是支持向量
间隔:
在样本空间中,任意点到超平面的距离为:
例如在三位空间中,点到平面距离公式为:
在支持向量中,这项是为1的,所以两个虚线之间的距离为:
,这一项被称之为间隔
目标:
有了以上概念,我们的目标是:
希望最大化间隔,并且超平面满足约束条件
而最大化间隔,可以等价为最小化
,又因为
始终为正值,但是带根号,所以简化为找到
的最小值(1/2的系数是为了方便求导)。
所以优化目标为:
软间隔:
当然以上条件都是在数据集线性可分的基础之上,才能这么去想的,而实际上,很少有数据集可以完美的符合线性可分的条件,所以要引入软间隔。
引入软间隔后,约束条件从,变成了
,其中
叫做松弛变量。
有了松弛变量后,就允许了一部分点可以被错误的分类。当然,我们希望松弛变量也是越小越好。
具体点说就是:
当
时,代表该样本点是正确分类的。
当
时,代表该样本点分类虽然时正确的,但是是在自己标签的分离间隔和超平面之间的。
当
时,代表该样本点在超平面上,无法正确分类。
当
时,代表该样本点被错误分类了。
所以目标函数就变为:
,其中C是认为给出的正则化参数,用于控制
的大小。
把这个式子写成损失函数,就变成了以下形式,我们最小化损失函数即可。
,其中
对w求偏导,
当时,
,所以梯度为
当时,
,所以梯度为
梯度下降法:
若使用梯度下降法的SVM,权重更新式子为:
当时,
当时,
别的方法:
拉格朗日函数:
线性不可分的支持向量机的拉格朗日函数可以写为:
原始问题:
因为满足KKT条件(不去深究),所以可以将这个原始问题转化为对偶问题:
,意思是先对
求极小值,在对
求极大值。
为了让L得到极小值,接下来分别求偏导,并且令偏导数=0。
对w求偏导得到:
,
对b求偏导得到:
,
对求偏导得到:
,
将上述3个结果代入原式,得到这个式子:
,并且满足:
,
在上述条件下,解出,将其代入w和b中,就可以解出w和b了。
SMO算法:
解出上面的就是SMO算法优化的地方。
SMO 算法通过不断选择两个变量进行优化,固定其他变量,然后在选定的两个变量上优化目标函数,从而实现对目标函数的最大化。这个过程中,SMO 算法会不断地更新拉格朗日乘子 α,直到达到收敛条件,最终求出α。
理论过程对本人来说太难了,写不出来,望老师见谅。
核函数:
核函数的作用是将输入空间中的数据映射到一个高维特征空间,从而产生了新的特征矩阵,使得原始数据在新的特征空间中变得线性可分或更容易进行线性划分。这样做的目的是为了解决原始特征空间中线性不可分的问题。
有:线性核函数(Linear Kernel),多项式核函数(Polynomial Kernel),高斯核函数(Gaussian Kernel 或 RBF Kernel),其中高斯核函数是最常用的。
二、代码
梯度下降法:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# 加载鸢尾花数据集
iris = load_iris()
X = iris.data[:, :2] # 只使用两个特征
y = iris.target
# 将标签转换为二元分类问题(假设类别 0 作为正例,其他类别作为负例)
y = np.where(y == 0, 1, -1)
# 将数据集分割为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 特征缩放
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# 初始化模型参数
np.random.seed(42)
w = np.random.randn(X_train.shape[1]) # 权重
b = 0 # 偏置项
lr = 0.01 # 学习率
epochs = 100 # 迭代次数
lmd = 0.1
# 定义损失函数(hinge loss)
def hinge_loss(X, y, w, b):
loss = 1 - y * (np.dot(X, w) + b)
return np.maximum(0, loss)
# 训练 SVM 模型
cnt = 0
for epoch in range(epochs):
for i, x_i in enumerate(X_train):
if y_train[i] * (np.dot(x_i, w) + b) >= 1: # 判断是否分类正确
dw = 2 * lmd * w
else:
dw = 2 * lmd * w - np.dot(y_train[i], x_i) # 对于错误分类的样本,更新权重和偏置项
db = -y_train[i]
w -= lr * dw
b -= lr * db
cnt+=1
if cnt%100 == 0:
print(repr('更新了第') + repr(cnt) + repr('次') + repr('W:') + repr(w) + repr(' b:') + repr(b))
# 绘制决策边界
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=plt.cm.Paired)
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
# 创建网格以绘制决策边界
xx, yy = np.meshgrid(np.linspace(xlim[0], xlim[1], 50),
np.linspace(ylim[0], ylim[1], 50))
Z = np.dot(np.c_[xx.ravel(), yy.ravel()], w) + b
Z = np.sign(Z)
Z = Z.reshape(xx.shape)
# 绘制决策边界
plt.contour(xx, yy, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'], interpolation='nearest')
plt.xlabel('x1')
plt.ylabel('x2')
plt.title('result')
plt.show()
y_pred_train = np.sign(np.dot(X_train, w) + b)
y_pred_test = np.sign(np.dot(X_test, w) + b)
accuracy_train = np.mean(y_pred_train == y_train)
accuracy_test = np.mean(y_pred_test == y_test)
print("训练集准确率:", accuracy_train)
print("测试集准确率:", accuracy_test)
说明:
if y_train[i] * (np.dot(x_i, w) + b) >= 1:
dw = 2 * lmd * w
else:
dw = 2 * lmd * w - np.dot(y_train[i], x_i)
db = -y_train[i]
w -= lr * dw
b -= lr * db最关键的部分就是这里了,但是这里在上面理论部分的梯度下降法里头说明了,dw是L对w求偏导,db同理,lr是学习率,这个条件的意义是:当在当前超平面下,分割出来的当前这个样本点如果是正确的,并且处于间隔外,在惩罚中就不需要加入松弛参数变出的那一项。
三、结果:
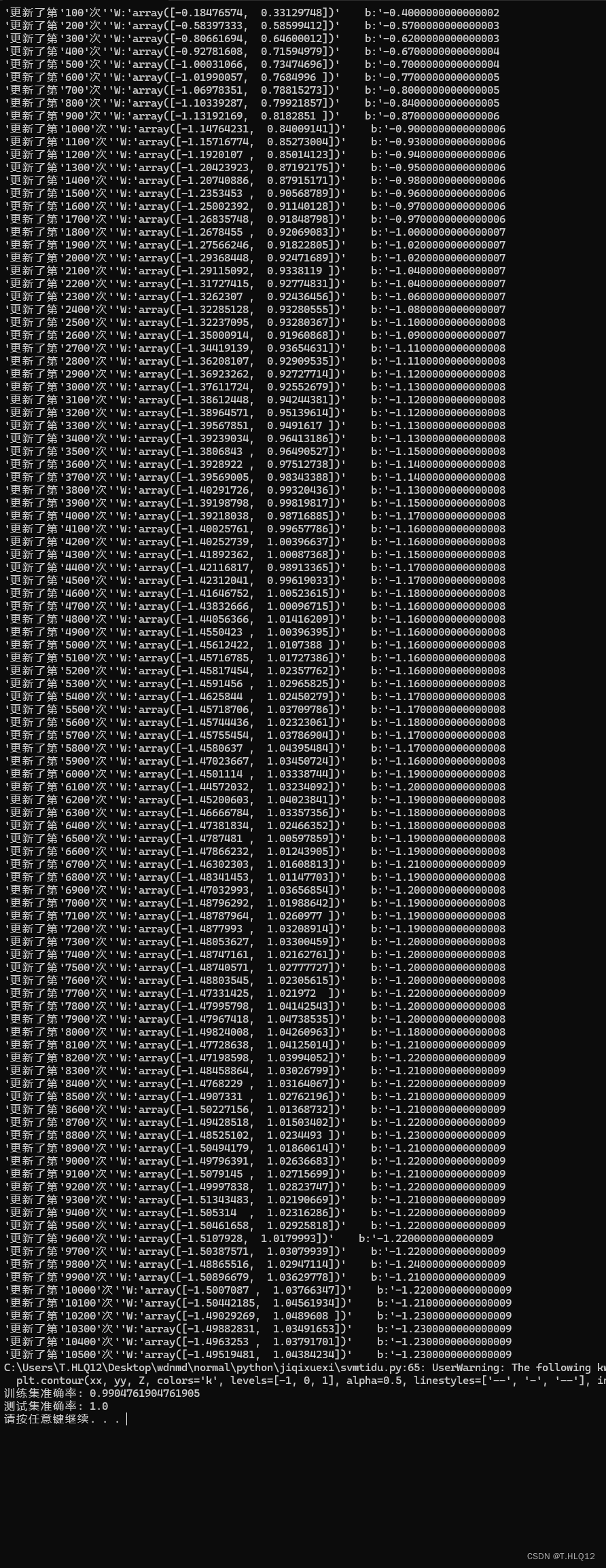
可以看到,在更新次数为9000左右的时候,参数就稳定下来了。
训练结果如下图:
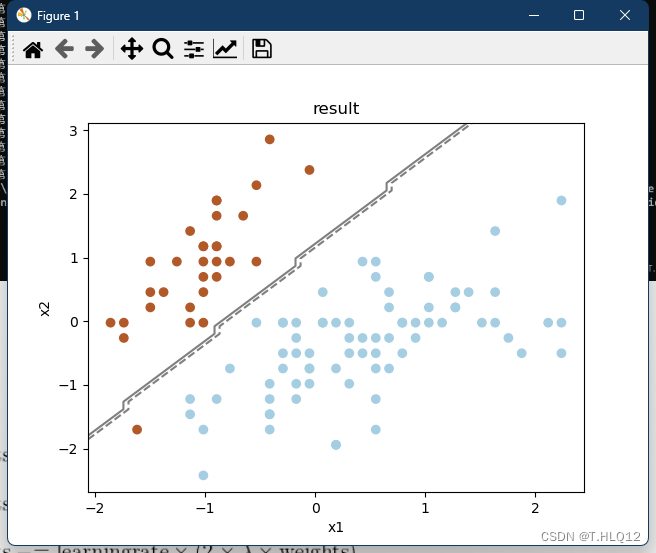

可以看到,有一个点虽然被错误分类了,但关系到总体,情况还是很好的。
优缺点分析:
梯度下降SVM:
优点:
- 全局最优解:梯度下降算法可以收敛到全局最优解(如果学习率合适,并且损失函数是凸函数),从而得到最佳的分类超平面。
- 易于实现:梯度下降算法的实现相对简单,只需计算损失函数关于模型参数的梯度,并根据梯度方向更新参数即可。
- 扩展性强:梯度下降算法可以轻松地扩展到大规模数据集和高维特征空间。
缺点:
- 学习率选择:梯度下降算法的性能高度依赖于学习率的选择。学习率太小会导致收敛速度慢,学习率太大可能会导致震荡或无法收敛。
- 局部最优解:在非凸损失函数的情况下,梯度下降算法可能会陷入局部最优解,而无法找到全局最优解。
- 对初始值敏感:梯度下降算法的性能受初始参数值的影响,不同的初始值可能会导致不同的收敛结果。
遇到的问题:
一开始把梯度下降法和SMO算法混起来了,主要是对梯度下降的损失函数和W的更新式子不知道怎么得出的,然后先去学了一遍拉格朗日函数,在看SMO理论的时候,感觉很难,不太像是梯度下降,回头多看了看最开始得出的目标函数,发现将松弛参数用超平面代入,再对W求偏导就可以得出W的更新式子了,梯度下降的问题就解决了。
关于SMO,理不清楚原理,还是不写了。。(上次实验课腾讯会议里头的代码应该是梯度下降法)
参考的视频:
视频1
视频2
视频3