MPC控制算法简化版
模型预测控制(Model Predictive Control,MPC)是一种先进的控制策略,广泛应用于人形机器人的运动控制。具体实现过程中,还需结合机器人的实际动力学模型和更多的物理约束条件。以下是一个人形机器人应用MPC算法的简要示例:
示例:使用MPC控制人形机器人行走
1. 系统建模
首先,需要建立人形机器人的动力学模型。这包括机器人的关节角度、角速度、关节力矩等状态变量,以及这些状态变量之间的动力学关系。
2. 定义控制目标
定义机器人的控制目标,例如在保持平衡的同时,让机器人以一定的速度向前行走。
3. 构建MPC优化问题
MPC的核心是解决一个优化问题,以预测未来一段时间内的系统行为,并计算出最优的控制输入。具体步骤如下:
- 1、预测模型:利用动力学模型预测未来时刻机器人的状态。
- 2、滚动优化:在每个控制周期内,解决以下优化问题:
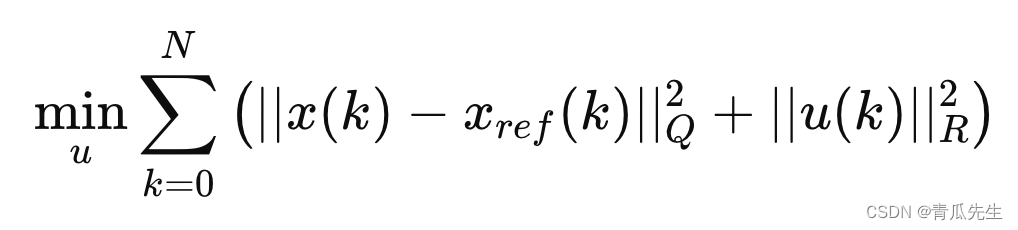
其中,x(k) 是第 k 时刻的状态向量,x𝑟𝑒𝑓(k) 是参考状态向量,u(k) 是控制输入,Q和R是权重矩阵,N 是预测时域长度。 - 3、约束条件:加入系统的物理约束,如关节角度、关节力矩的限制,以及避免与障碍物碰撞的约束。
4. 实时控制
在每个控制周期,进行以下步骤:
- 1、状态测量:测量当前机器人的状态 x(t)。
- 2、优化求解:利用当前状态作为初始条件,求解MPC优化问题,得到最优的控制输入序列 u∗(t),u∗(t+1),…,u∗(t+N)。
- 3、施加控制:施加第一个控制输入 u∗(t) 给机器人。
- 4、滚动窗口:更新状态并重复上述过程。
5. 仿真与验证
通过仿真验证MPC算法的有效性,确保机器人能够按照预定的轨迹行走,并能在面对外部扰动时保持稳定。
代码示例
以下是一个简化的MPC控制人形机器人步态的Python代码示例,使用常见的MPC库如CasADi进行实现:
import casadi as ca
import numpy as np
# 定义系统动力学模型
def robot_dynamics(x, u):
# 简化的动力学模型
x_next = x + u
return x_next
# MPC参数
N = 10 # 预测时域
Q = np.eye(2)
R = np.eye(1)
# 初始状态
x0 = np.array([0, 0])
# 状态和控制变量
x = ca.SX.sym('x', 2)
u = ca.SX.sym('u', 1)
# 优化变量
X = ca.SX.sym('X', 2, N+1)
U = ca.SX.sym('U', 1, N)
# 初始状态约束
constr = [X[:, 0] == x0]
# 目标函数
obj = 0
for k in range(N):
x_next = robot_dynamics(X[:, k], U[:, k])
constr += [X[:, k+1] == x_next]
obj += ca.mtimes([(X[:, k] - x0).T, Q, (X[:, k] - x0)]) + ca.mtimes([U[:, k].T, R, U[:, k]])
# 优化器
nlp = {'x': ca.vertcat(ca.reshape(X, -1, 1), ca.reshape(U, -1, 1)),
'f': obj,
'g': ca.vertcat(*constr)}
solver = ca.nlpsol('solver', 'ipopt', nlp)
# 初始猜测
x_guess = np.zeros((2, N+1))
u_guess = np.zeros((1, N))
sol = solver(x0=ca.vertcat(ca.reshape(x_guess, -1, 1), ca.reshape(u_guess, -1, 1)),
lbg=0, ubg=0)
# 提取最优控制输入
optimal_u = np.array(sol['x'][-N:]).flatten()
print("Optimal control input: ", optimal_u)