注册wildcard(虚拟卡)
注册号账号后先进行充值,充值后选择CHATGPT一键升级按照他的流程来即可
Wildcard网址:Wildcard跳转注册
填写邀请码充值时少两美金合计14¥
邀请码:OL3QXTRH
CHATGPT升级plus(已有账号前提下)
news2026/2/12 15:58:00
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1802291.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
Adobe Illustrator 矢量图设计软件下载安装,Illustrator 轻松创建各种矢量图形
Adobe Illustrator,它不仅仅是一个简单的图形编辑工具,更是一个拥有丰富功能和强大性能的设计利器。 在这款软件中,用户可以通过各种精心设计的工具,轻松创建和编辑基于矢量路径的图形文件。这些矢量图形不仅具有高度的可编辑性&a…
Codeforces Round 951 (Div. 2)
A - Guess the Maximum
直接暴力枚举 a i , a i 1 a_i,a_{i1} ai,ai1找最小的最大值 答案即为最小的最大值-1
code: #include<bits/stdc.h>
#define endl \n
#define fast() ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr)
#define F first
#…
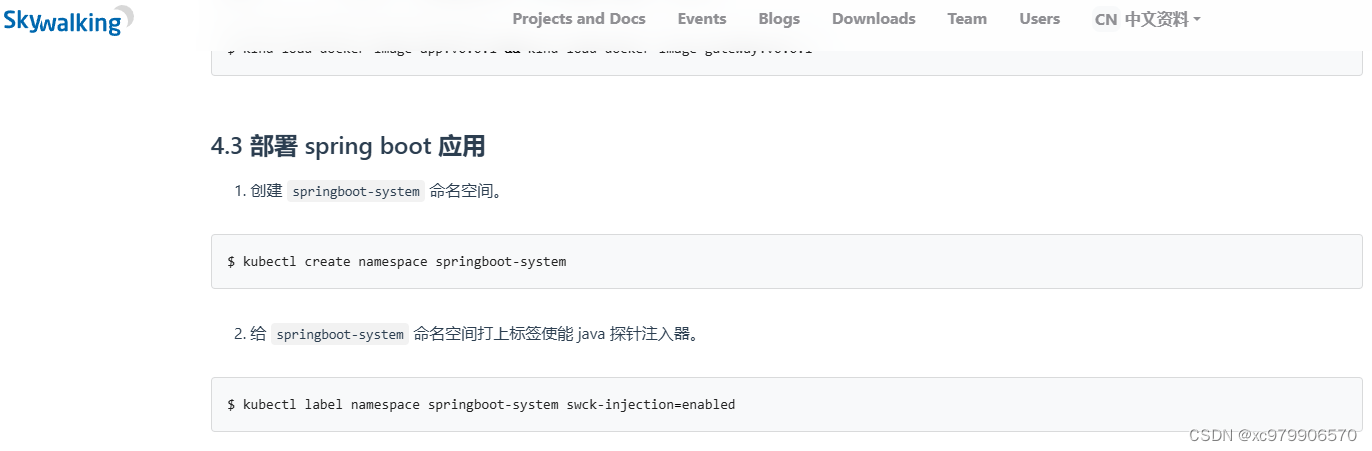
skywalking学习
文章目录 前言一、skywalking单体安装部署1. 下载skywalking2. 部署oap和oap-ui服务3. 测试skywalking监控springboot应用 二、搭建swck(skywalking集群)1.安装k8s2.下载swck3.设置pod自动注入java agent 三、skywalking监控python四、skywalking监控cpp总结参考 前言
本文主要…
RTKLIB之RTKPLOT画图工具
开源工具RTKLIB在业内如雷贯耳,其中的RTKPLOT最近正在学习,发现其功能之强大,前所未见,打开了新的思路。
使用思博伦GSS7000卫星导航模拟器,PosApp软件仿真一个载具位置
1,RTKPLOT支持DUT 串口直接输出的NMEA数据并…
HCL模拟器下做M-LAG测试(以及和华为配置对比)-二层架构
1.简单二层架构
1.1 拓扑图 1.2 配置
1.2.1 Leaf1配置 system-mac必须配置,否则会有一个node处于unknown状态,即使配置主节点的mac,主节点也需要配置system-mac为自己的mac ## M-LAG配置[Leaf1] m-lag system-mac 0001-0001-0001 # 手动设…
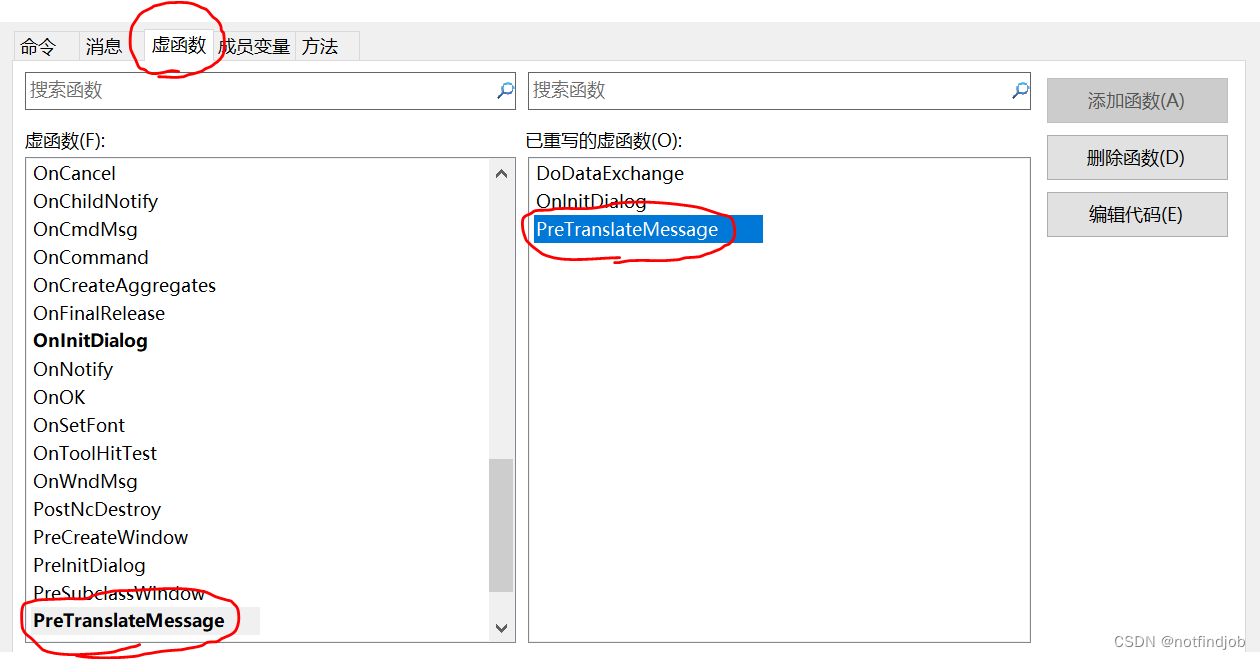
MFC 教程-回车时窗口退出问题
【问题描述】
MFC窗口默认时,按回车窗口会退出
【原因分析】
默认调用OnOK()
【解决办法】
重写虚函PreTranslateMessage BOOL CTESTMFCDlg::PreTranslateMessage(MSG* pMsg)
{// TODO: 在此添加专用代码和/或调用基类// 修改回车键的操作反应 if (pMsg->…
物理安全防护如何创新强化信息安全体系?
物理安全防护是信息安全体系的重要组成部分,它通过保护实体设施、设备和介质等,防止未授权访问、破坏、盗窃等行为,从而为信息系统提供基础的安全保障。要创新强化信息安全体系中的物理安全防护,可以从以下几个方面着手࿱…
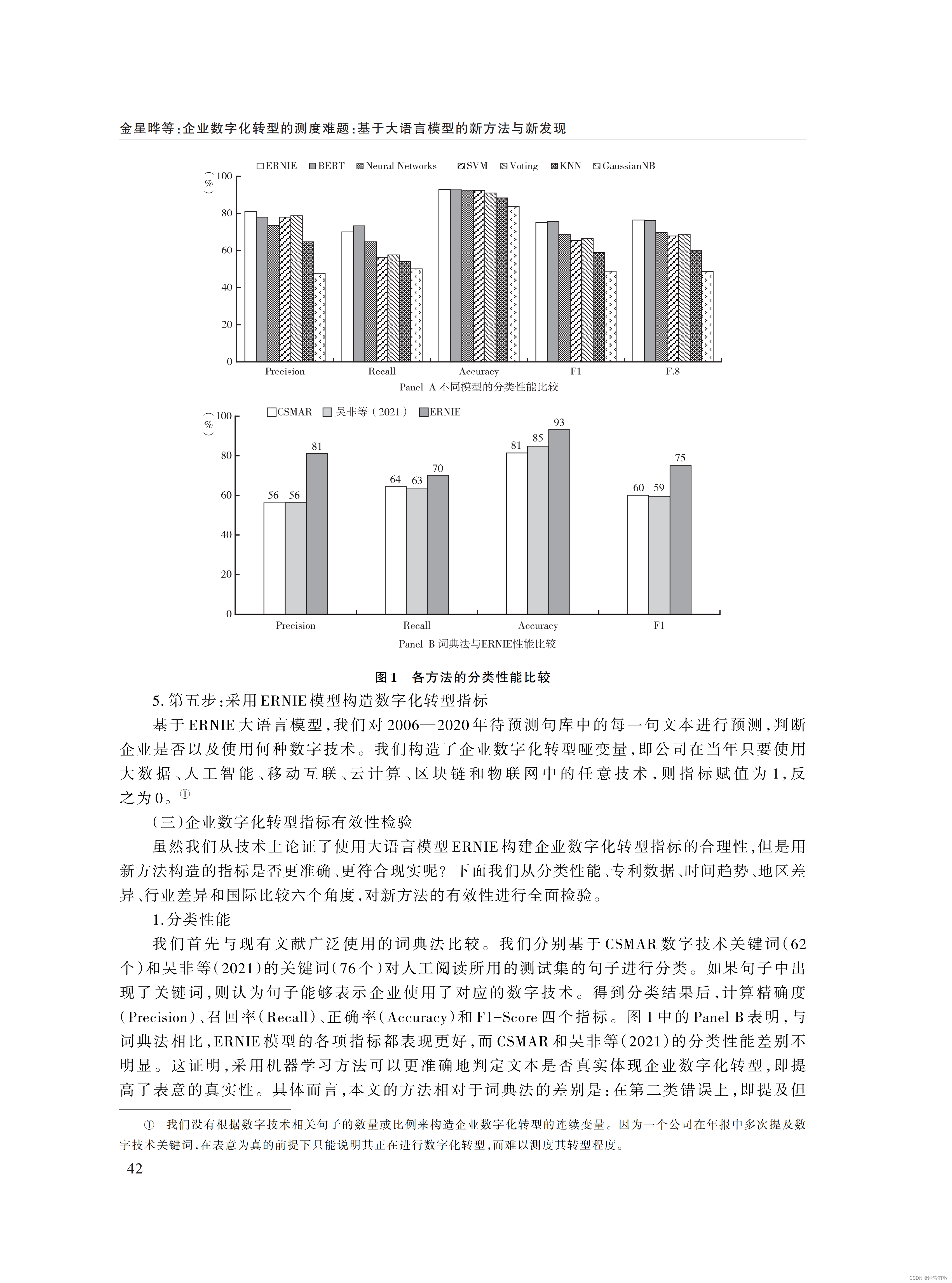
企业数字化转型的测度难题:基于大语言模型的新方法与新发现
《经济研究》新文章《企业数字化转型的测度难题:基于大语言模型的新方法与新发现》运用机器学习和大语言模型构造一套新的企业数字化转型指标。理论分析和数据交叉验证均表明,构建的指标相对已有方法更准确:
1.第一步:选择“管理…
Redis常用命令——List篇
提到List,我们第一时间想到的就是链表。但是在Redis中,List更像是一种双端队列,例如C中的deque。它可以快速高效的对头部和尾部进行插入和删除操作。本片文章主要对List列表的相关命令进行详解,希望本篇文章会对你有所帮助。 文章…
js--hasOwnProperty()讲解与使用
@TOC
前言 hasOwnProperty(propertyName)方法 是用来检测属性是否为对象的自有属性 object.hasOwnProperty(propertyName) // true/false 讲解 hasOwnProperty() 方法是 Object 的原型方法(也称实例方法),它定义在 Object.prototype 对象之上,所有 Object 的实例对象都会继…
高考志愿选专业,如何分析自己的兴趣爱好?
之所以在选择专业的时候比较迷茫,就是对自己不够了解,没有分析过自己的兴趣爱好,所以也不知道如何选择适合自己的专业,但是他们又不得不做出更深入的了解,因为专业的选择将关系到未来的职业道路和生活方向。
对于绝大…
java 大型企业MES生产管理系统源码:MES系统与柔性化产线控制系统的关系、作用
MES定义为“位于上层的计划管理系统与底层的工业控制之间的面向车间层的管理信息系统”,它为操作人员/管理人员提供计划的执行、跟踪以及所有资源(人、设备、物料、客户需求等)的当前状态。
MES系统与柔性化产线控制系统的关系
MES(制造执行系统)是一种…
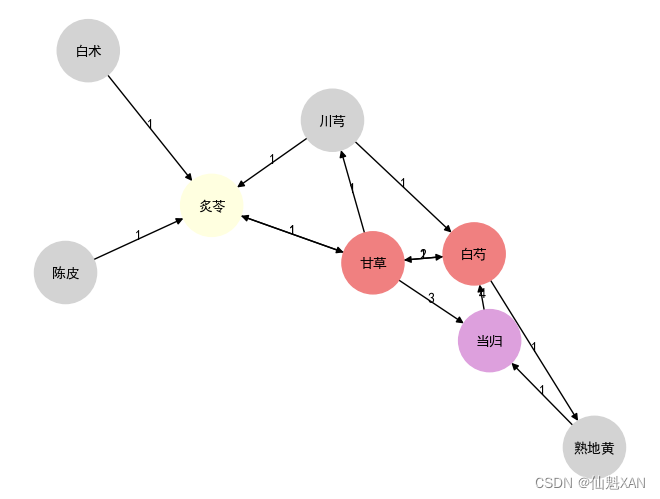
Python 机器学习 基础 之 【实战案例】中药数据分析项目实战
Python 机器学习 基础 之 【实战案例】中药数据分析项目实战 目录
Python 机器学习 基础 之 【实战案例】中药数据分析项目实战
一、简单介绍
二、中药数据分析项目实战
三、数据处理与分析实战
1、数据读取
2、中药材数据集的数据处理与分析
2.1数据清洗
2.2、 提取别…
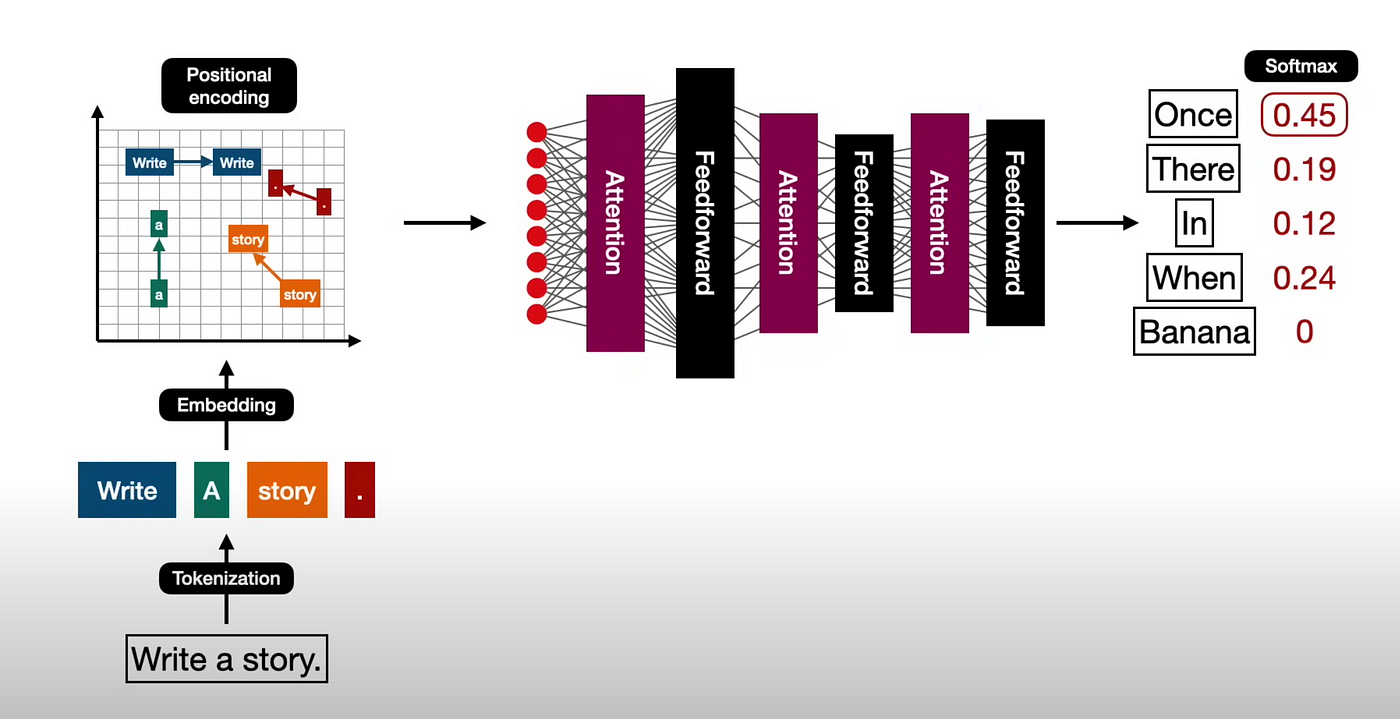
什么是大型语言模型 ?
引言 在本文[1]中,我们将从高层次概述大型语言模型 (LLM) 的具体含义。 背景 2023年11月,我偶然间听闻了OpenAI的开发者大会,这个大会展示了人工智能领域的革命性进展,让我深深着迷。怀着对这一领域的浓厚兴趣,我加入了…
计算机网络--计算机网络概念
计算机网络--计算机网络概念
计算机网络--物理层
计算机网络--数据链路层
计算机网络--网络层
计算机网络--传输层
计算机网络--应用层
0.计算机网络简介 0.2 计算机网络的功能简介
数据通信(连通性)资源共享: 软件硬件数据
分布式处理 多台计算机各自承担同…
每日一题——Python实现PAT甲级1015 Reversible Primes(举一反三+思想解读+逐步优化)
一个认为一切根源都是“自己不够强”的INTJ
个人主页:用哲学编程-CSDN博客专栏:每日一题——举一反三Python编程学习Python内置函数
Python-3.12.0文档解读
目录
我的写法
is_prime函数分析:
decimal_to_base函数分析:
主循…
Segment Anything
参考:【图像分割】Segment Anything(Meta AI)论文解读-CSDN博客
背景
提示分割任务:在给定任何分割提示下返回一个有效的分割掩码目标:开发一个可提示的图像分割的基础模型,在一个广泛的数据集上预训练&a…
【网络安全的神秘世界】在win11搭建pikachu靶场
🌝博客主页:泥菩萨 💖专栏:Linux探索之旅 | 网络安全的神秘世界 | 专接本 下载pikachu压缩包
https://github.com/zhuifengshaonianhanlu/pikachu 下载好的pikachu放在phpstudy_pro/www目录下 创建pikachu数据库 打开phpstudy软件…
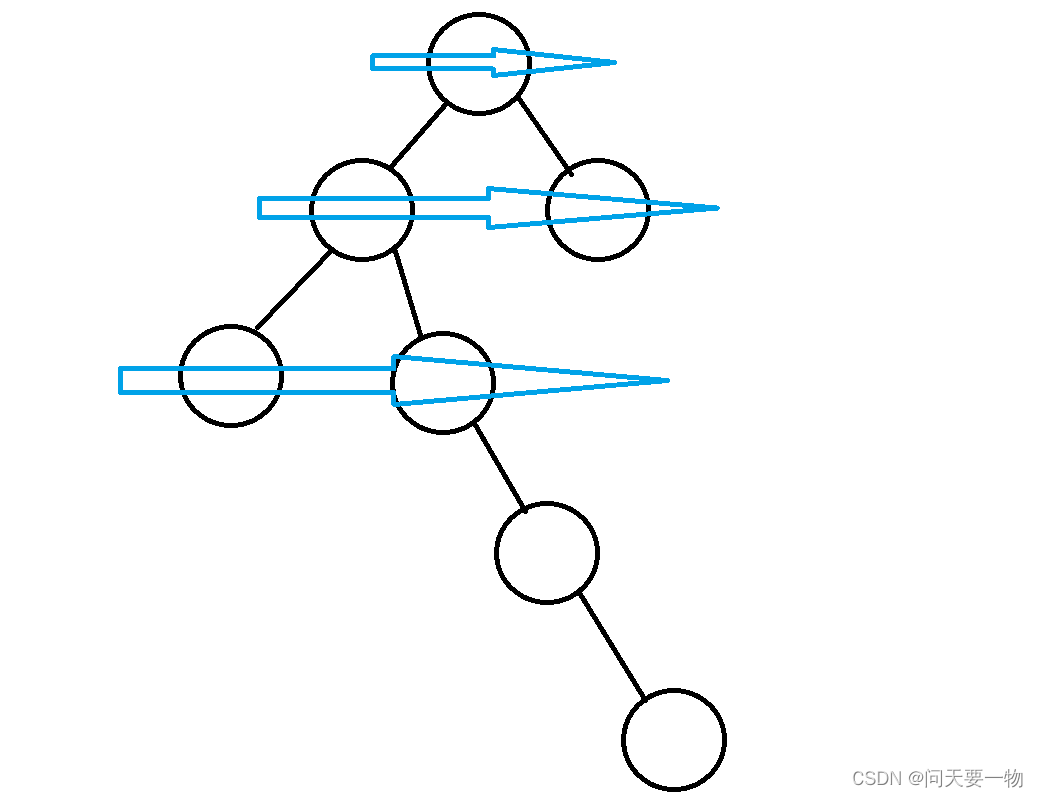
数据结构--二叉树(二)
链式二叉树 链式二叉树是链式树集合中的一种,该树的每个根节点最多只有两个孩子节点,我们一般用左右孩子来称呼,在初学链式二叉树时,由于大家对链式二叉树的结构掌握还不够深入,为了降低本章的学习难度及成本ÿ…