FA-GAN: Fused attentive generative adversarial networks for MRI image super-resolution

（FA-GAN：融合注意生成对抗网络的MRI图像超分辨率）

高分辨率磁共振图像可以提供细粒度的解剖信息，但是获取这样的数据需要长的扫描时间。本文提出了一种融合衰减生成对抗网络（FA-GAN）框架，用于从低分辨率磁共振图像生成超分辨率磁共振图像，该框架可以有效地减少扫描时间，但需要高分辨率磁共振图像。在FA-GAN的框架下，提出了一种局部融合特征块，该特征块由使用不同卷积核的不同三通道网络组成，用于提取不同尺度下的图像特征。设计了全局特征融合模块，包括通道注意模块、自注意模块和融合操作，用于增强MR图像的重要特征。此外，为了使鉴别器网络稳定，还引入了谱归一化处理。利用40组3D磁共振图像（每组图像包含256个切片）对网络进行训练，并利用10组图像对所提方法进行测试。实验结果表明，与现有的重构方法相比，提出的FA-GAN方法生成的超分辨磁共振图像的PSNR和SSIM值均有所提高。

介绍

图像超分辨率指的是从低分辨率图像重建高分辨率图像。高分辨率意味着图像中的像素更密集并且可以显示更灵活的细节。这些细节在实际应用中非常有用，例如卫星成像、医学成像等，它们可以更好地识别目标并在高分辨率图像中发现重要特征。高分辨率（HR）MRI图像可提供精细的解剖信息，有助于临床诊断和准确决策。但它不仅需要昂贵的设备，而且需要较长的扫描时间，给图像数据采集带来了挑战。因此，进一步的应用受限于缓慢的数据采集和成像速度。超分辨率（SR）是从单个或一组低分辨率（LR）图像生成高分辨率（HR）图像的技术，其可以提高图像细节的可见性或恢复图像细节。在不改变硬件或扫描组件的情况下，SR方法可以显著提高MRI的空间分辨率。通常，在MRI中实现图像SR的方法有三种：基于插值、基于构造和基于机器学习。基于内插的SR技术假设LR图像中的区域可以通过使用多项式或具有先验平滑度的内插函数而扩展到对应区域。基于插值的超分辨率重建算法具有算法简单、实时性高的优点;其缺点是过于简单，不能充分利用MR图像的先验信息。特别是基于单幅MR图像的超分辨率重建算法存在明显的缺点。
引入基于重构的SR方法来解决包含两项的优化问题：保真度项，其惩罚退化的SR图像和观察到的LR图像之间的差异;以及正则化项，其促进稀疏性和恢复SR信号的固有特性。当输入数据变得太稀疏或模型变得甚至稍微不准确时，这些技术的性能变得次优，特别是在高频区域。这些缺点降低了基于重建的SR方法对大放大倍数的效果，其对于小于4的小放大倍数可能工作良好。
机器学习技术，特别是基于深度学习（DL）的SR方法，由于其在自然图像的SR中的最新性能，最近吸引了相当大的关注。最新的算法依赖于数据驱动的深度学习模型来重构精确超分辨率所需的细节。基于深度学习的方法旨在直接从训练样本自动学习输入和输出之间的关系。与此同时，深度学习在CT/PET图像重建中也发挥了至关重要的作用，如从正弦图域重建PET图像。
随着深度学习技术的发展，Goodfellow等人提出的生成式对抗网络（Generative Adversarial Network，GAN）在图像变换和超分辨率成像方面表现出良好的性能。Sanchez等人提出了用于生成脑超分辨率图像的标准超分辨率GAN（SRGAN）框架。大多数基于GAN的图像生成模型是使用卷积层来构造的。卷积处理局部邻域中的信息，然而，仅使用卷积层在建立图像中的远程依赖性方面是低效的。
使用小的卷积核很难学习图像之间的依赖性。然而，卷积核的大小太大，这将降低模型的性能。此外，增加卷积核的大小也可以扩大感受野，但不可避免地增加了模型的复杂性。Zhang等人提出了自我注意生成对抗网络（SAGAN），该网络具有注意力驱动的、用于图像生成任务的长范围依赖性建模。在先前关于重构问题的工作中，基于深度学习的方法具有两个主要问题。首先，它们同等地对待每个通道式特征，但是对于重建任务的贡献根据不同的特征图而不同。其次，卷积层中的感受野可能导致丢失来自原始图像的上下文信息，尤其是那些包含诸如边缘和纹理之类的有价值的详细信息的高频分量。为此，本文设计了通道注意模块来过滤无用特征，增强有用特征。因此，浅层中的模型参数大多数是与给定任务相关的更新。据我们所知，这是第一个将通道式注意力用于MRI重建问题的工作。结合MR重建和图像超分辨率的思想，一些研究人员致力于从低分辨率欠采样K空间数据直接恢复HR图像。
本文提出了一种融合注意生成对抗网络（FAGAN），用于从低分辨率MR图像生成超分辨率MR图像。

贡献

1）提出了局部融合特征块，该特征块由不同的三通道网络和不同的卷积核组成，用于提取不同尺度下的图像特征，以提高SR图像的重建性能;
2）设计了全局特征融合模块，包括通道注意模块、自注意模块和融合操作，增强了MRI图像的重要特征，使超分辨率图像更真实、更接近原始图像;
3）将谱归一化（SN）引入到鉴别器网络中，不仅平滑和加速了深度神经网络的训练过程，而且提高了模型的泛化性能。

方法

提出的神经网络模型设计为首先学习图像，然后将LR图像逆映射到参考HR图像。该模型仅以LR图像作为输入来生成SR图像。操作可定义为

SR network with GAN

网络输出通过一系列上采样阶段，其中每个阶段将输入图像大小加倍。输出通过卷积级以获得分辨的图像。取决于期望的缩放，可以改变上采样级的数目。对抗性min-max问题定义为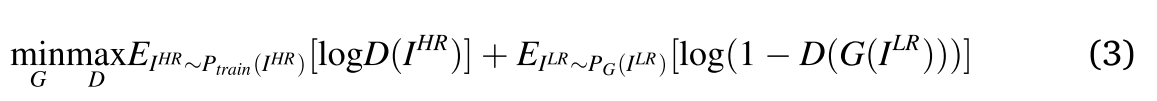
拟议FA-GAN网络的框架如图1所示。整个模型以下采样后的低分辨率磁共振图像为输入，通过LFFB模型提取特征，再经过卷积和上采样生成放大图像。最后，GFFB模块融合细节特征以生成超分辨率磁共振图像。在训练过程中，HR参考将用于指导模型参数的优化。此外，在鉴别器网络中引入了谱归一化（SN），以稳定GAN的训练。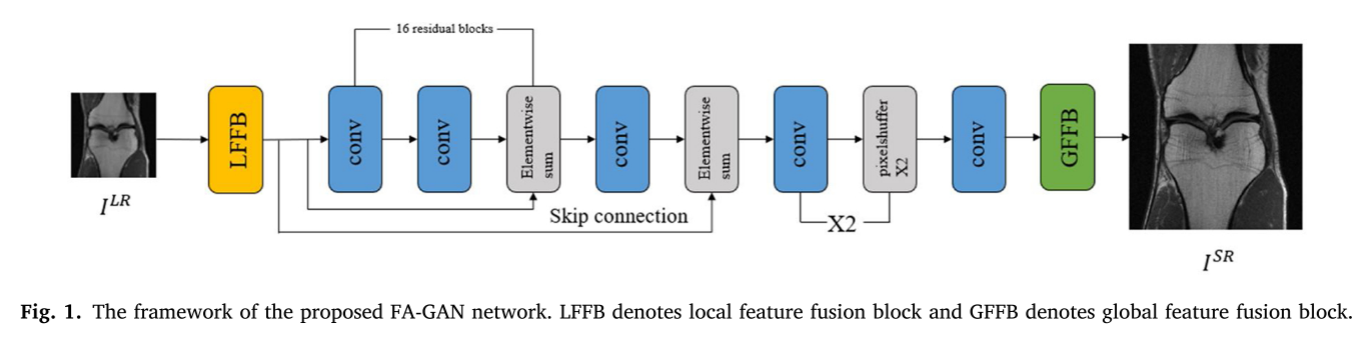

Local fusion feature block (LFFB)

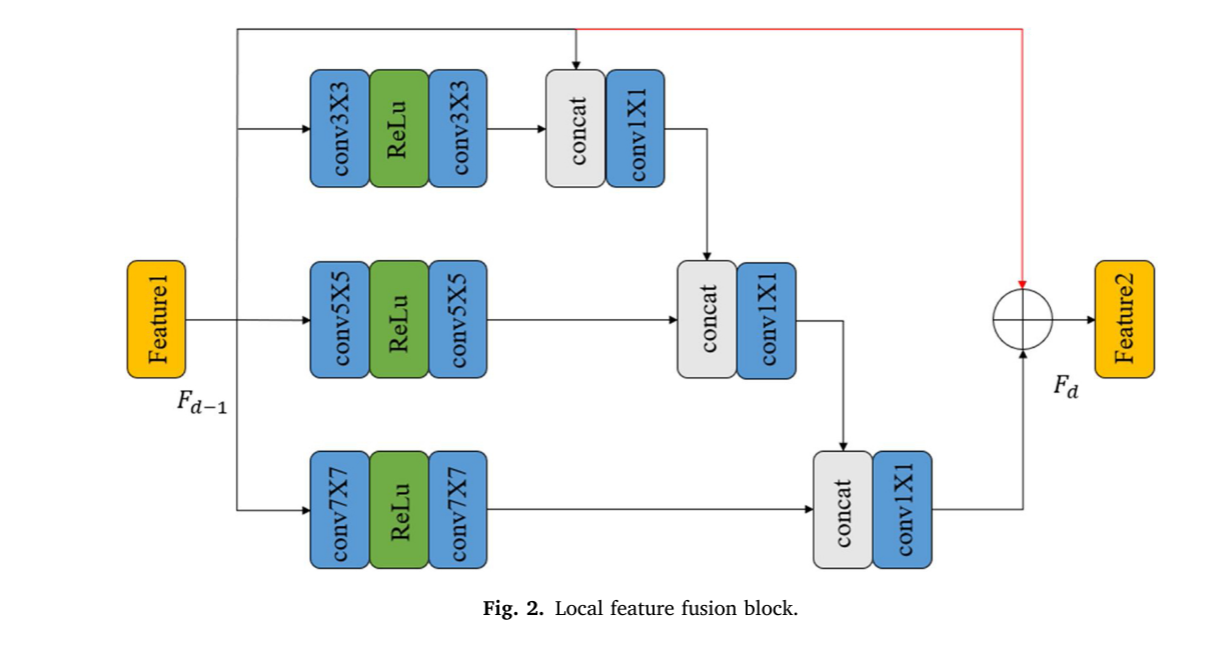
与Fu等人先前的实验不同，局部融合特征块由不同的三遍网络使用不同的卷积核组成，如图2所示。这样，这些支路之间的信息流可以相互共享，这使得我们的网络可以在不同的尺度上提取图像特征。操作可定义为

其中Cs × s表示S尺度特征提取器。提出的S尺度特征提取器由三层核大小为s × s的卷积层和一层ReLU中间激活层组成。F [∙]的运算意味着级联和1 × 1卷积，主要是为了快速融合特征，减少计算负担。

Global feature fusion block (GFFB)

全局特征融合模块包括信道关注模块、自关注模块和融合运算三部分。通过这些模块，可以增强MRI图像的重要特征，使超分辨率图像更加逼真，更接近原始图像（图3）。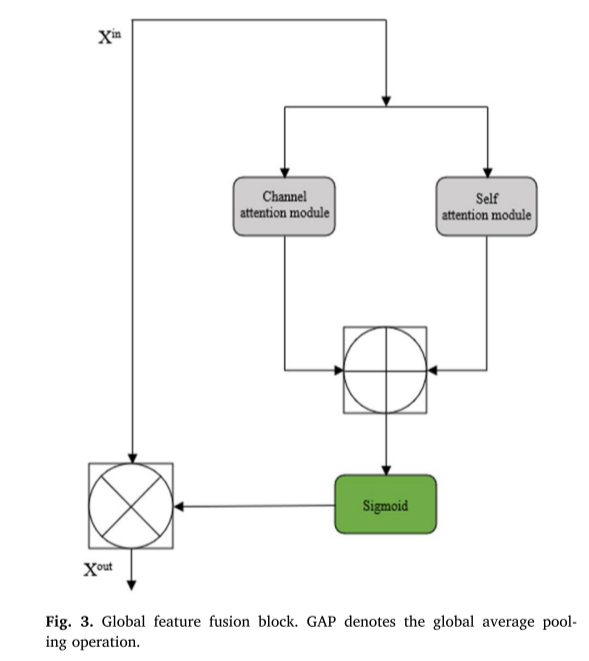

(1) Channel-Attention Module

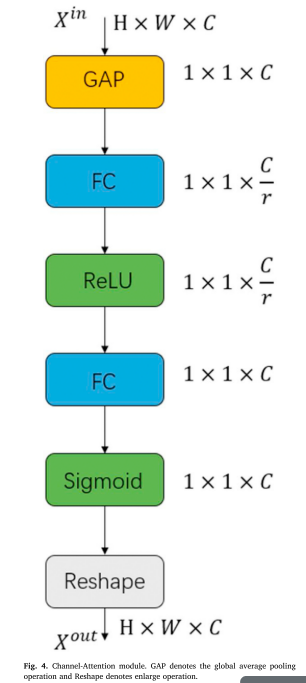
本文介绍了一种轻量级的信道注意机制，它允许通过一个一维向量从全局信息中选择性地强调有用特征和抑制无用特征。如图4所示，首先使用全局平均池来提取空间维度H*W上的全局信息。然后，接着是具有缩减率r的维度缩减层、ReLu激活、维度增加层和Sigmoid激活，以生成SR图像。实现两个维度可计算的层的完全连接层。最后输出的校准是通过重新调节输入功能。二维可计算层由全连通层实现。通过重新缩放输入特征来获取重新校准的最终输出。

(2) Self-Attention Module

自注意模块的作用是用自注意特征图代替传统的卷积特征图。
卷积运算后，卷积特征图经过1 × 1卷积结构的三个分支f(x)，g(x)，h(x)，特征图的大小不变。g(x)改变通道数，h(x)的输出保持通道数不变。H和W表示要素地图的长度和宽度，C表示通道数。将f(x)的输出转置后，乘以g(x)的输出矩阵，经过softmax归一化，得到[H * W，H * W]注意力图。将注意力图与h(x)的输出相乘得到[H*W，C]特征图，再用1 × 1卷积将输出整形为[H，W，C]得到此时的特征图。自注意模块的结构如图5所示。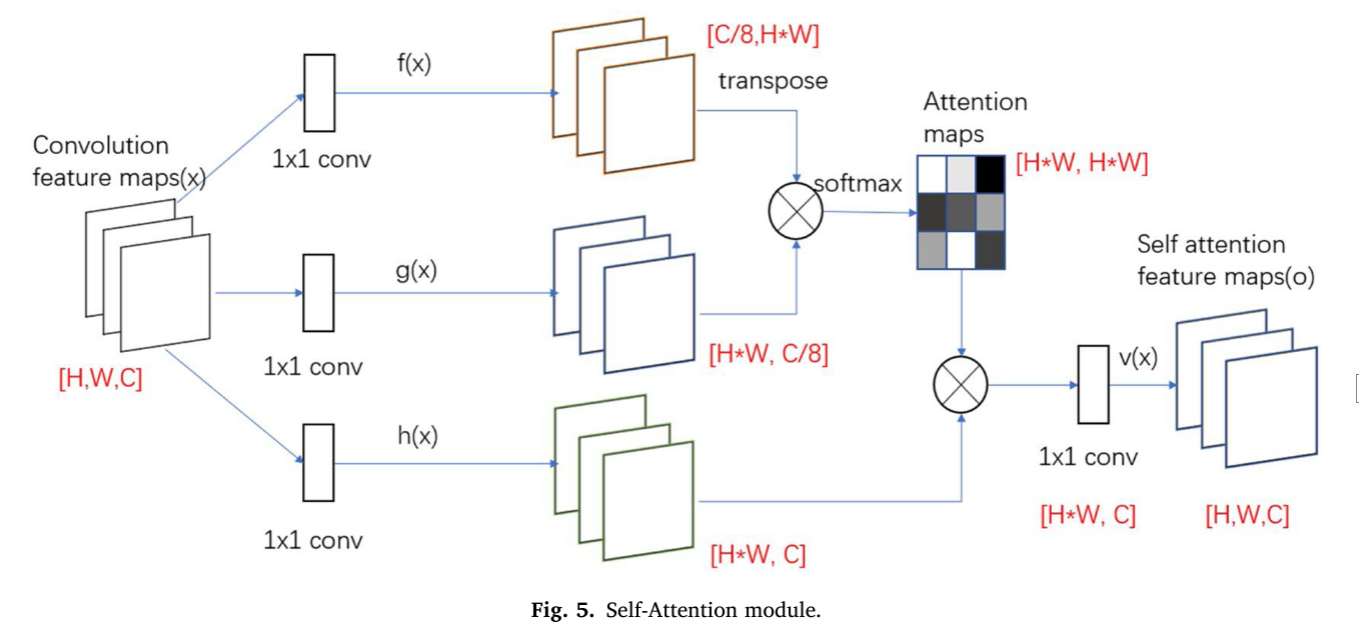

其中${\beta }^{j,i}$表示合成第$j^{th}$个区域时模型关注第$i^{th}$个位置的程度。这里，C是通道数，N是来自前一隐藏层的特征的特征位置数。
注意层的输出是o，并且可以表示为：

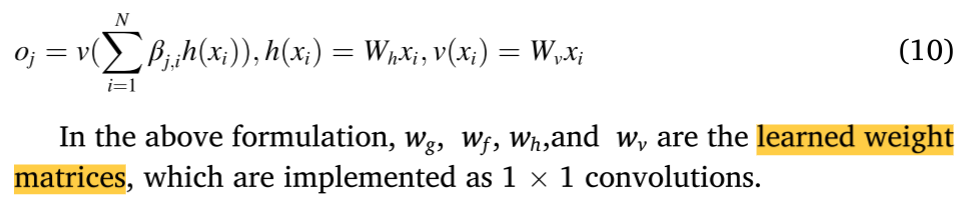
此外，我们进一步将注意层的输出乘以一个尺度参数，并加回输入特征图。因此，最终输出由下式给出：

其中γ是可学习的标量，初始化为0。引入可学习γ可以使网络首先依赖于局部邻域的信息，然后逐渐学习为非局部信息分配更多的权重。

(3) Fusion Operation**

A. Direct Connection
直接连接函数可以通过直接将两项相加来实现，如下所示：

其中i是特征的索引。R代表通道关注的输出，Y代表自我关注的输出。α和β均设置为0.5作为预设值。
B. Weighted Connection.
与直接连接相比，加权连接引入了R和Y之间的竞争。此外，该方法易于扩展为softmax形式，具有更强的鲁棒性，对平凡特征不敏感，α和β均取0.5作为预设值。为了避免引入额外的参数，我们使用R和Y计算权重。加权连接函数表示为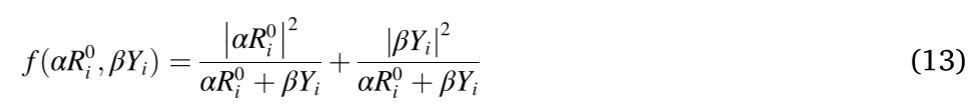

(4) Loss Function

损失函数用于估计由模型生成或拟合的值与真实的值之间的差异，即重建的MRI与原始MRI之间的差异。损失函数越小，模型越强。为了提高模型重建的质量，我们提出使用感知损失、像素损失和对抗损失作为发生器的组合损失函数。感知损失模仿人类视觉差异，而像素损失是图像域中像素之间的差异。
本文采用与人的感知更相关的VGG特征之间的欧几里德距离作为内容损失，如下所示：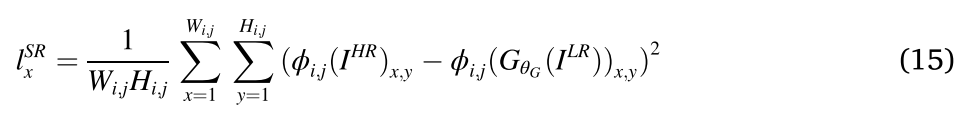
Φ_i,j指示所提取的特征是第i个最大池化层之前的第j个卷积层。W_i,j、H_i,j表示要素图层的维度。
对抗损失函数是由发生器产生的样本的平均鉴别器概率值。公式如下：