【资源限制】

内存限制：256.0MB   C/C++时间限制：1.0s   Java时间限制：3.0s   Python时间限制：5.0s

【问题描述】
        小蓝办了一个画展，在一个画廊左右两边陈列了他自己的作品。为了使画展更有意思，小蓝没有等距陈列自己的作品，而是按照更有艺术感的方式陈列。

        在画廊的左边陈列了 L 幅作品，在画廊的右边陈列了 R 幅作品，左边的作品距离画廊的起点依次为 u_1, u_2, · · · , u_L，右边的作品距离画廊起点依次为 v_1, v_2, · · · ,v_R。

        每周，小蓝要整理一遍自己的每一幅作品。整理一幅作品的时间是固定的，但是要带着沉重的工具。从一幅作品到另一幅作品之间的距离为直线段的长度。

        小蓝从画廊的起点的正中央（左右两边的中点）出发，整理好每一幅画，最终到达画廊的终点的正中央。已知画廊的宽为 w。

        请问小蓝最少带着工具走多长的距离？

【输入格式】
        输入的第一行包含四个整数 L,R,d,w，表示画廊左边和右边的作品数量，以及画廊的长度和宽度。

        第二行包含 L 个正整数 u_1, u_2, · · · , u_L，表示画廊左边的作品的位置。

        第三行包含 R 个正整数 v_1, v_2, · · · , v_R，表示画廊右边的作品的位置。

【输出格式】
输出一个实数，四舍五入保留两位小数，表示小蓝最少带着工具走的距离。

【样例输入】

3 3 10 2
1 3 8
2 4 6

【样例输出】

14.71
【样例说明】

        小蓝从起点开始，首先到达左边第一幅作品（走动距离√2)，然后到达左边第二幅作品（走动距离2)，然后到达右边第一幅作品〈走动距离√5>，然后到达右边第二幅和第三幅作品〈走动距离2和2)，然后到达左边第三幅作品(走动距离2v2)，最后到达画廊终点（走动距离 √5)。

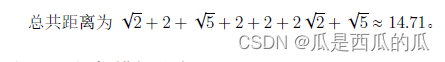
【思路与分析】

        先说结论，该题本质上就是一道动态规划的题目。首先需要定义一个三维数组，记录每次的状态。

dp[i][j]表示处理完左边第1幅画和右边第j幅画所走的最小路程，但是我们无法知道“现在”到底在左边还是在右边，所以我们还需要增加一维数组代表“现在”所处的状态，0在左，1在右。

动态规划最重要的就是要写出状态转移方程。

        例如现在我们要到达左边，有两种可能性：初始状态在左、初始状态在右。那么我们的状态转移方程为：

dp[i][j][0]=Math.min(dp[i][j][0],Math.min(dp[i-1][j][0]+left[i]-left[i-1], dp[i-1][j][1]+js(left[i],right[j],l)));

【代码：官方题解】

import java.util.*;
 
public class Main{
 
    public static double getDistance(int[] point1, int[] point2) {
        int x_diff = point1[0] - point2[0];
        int y_diff = point1[1] - point2[1];
 
        return Math.sqrt(x_diff * x_diff + y_diff * y_diff);
    }
 
    public static void main(String[] args) {
        final double INF = 1e9;
        Scanner sc = new Scanner(System.in);
        String[] firstLine = sc.nextLine().split(" ");
        int n = Integer.parseInt(firstLine[0]);
        int D = Integer.parseInt(firstLine[1]);
 
        int[][] points = new int[n][2];
 
        for (int i = 0; i < n; i++) {
            String[] line = sc.nextLine().split(" ");
            int x = Integer.parseInt(line[0]);
            int y = Integer.parseInt(line[1]);
            points[i][0] = x;
            points[i][1] = y;
        }
 
        double[][] distances = new double[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                double distance = getDistance(points[i], points[j]);
                if (distance > D) {
                    distances[i][j] = INF;
                    distances[j][i] = INF;
                } else {
                    distances[i][j] = distance;
                    distances[j][i] = distance;
                }
            }
        }
 
        for (int k = 0; k < n; k++) {
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    distances[i][j] = Math.min(distances[i][j], distances[i][k] + distances[k][j]);
                }
            }
        }
 
        double[][] f = new double[1 << n][n];
        for (int i = 0; i < 1 << n; i++) {
            for (int j = 0; j < n; j++) {
                f[i][j] = INF;
            }
        }
        f[1][0] = 0;
 
        for (int i = 0; i < (1 << n); i++) {
            for (int j = 0; j < n; j++) {
                if ((i >> j & 1) != 0) {        // i的比特位 里面包含 j
                    for (int k = 0; k < n; k++) {
                        if ((((i - (1 << j)) >> k) & 1) != 0) {     //  i 的比特位去掉 j 后包含k
                            f[i][j] = Math.min(f[i][j], f[i - (1 << j)][k] + distances[k][j]);
                        }
                    }
                }
            }
        }
 
        double ans = INF;
        for (int i = 0; i < n; i++) {
            ans = Math.min(ans, f[(1 << n) - 1][i] + distances[i][0]);
        }
 
        System.out.println(String.format("%.2f", ans));
 
    }
}

【代码】

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.Arrays;
 
public class Main {
 
	public static void main(String[] args) throws IOException {
		StreamTokenizer x=new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
		PrintWriter out=new PrintWriter(System.out);
		x.nextToken();
		int n=(int)x.nval;
		x.nextToken();
		int m=(int)x.nval;
		x.nextToken();
		int k=(int)x.nval;
		x.nextToken();
		int l=(int)x.nval;
		int INF = 0x3f3f3f3f;
		int left[]=new int[n+1];
		int right[]=new int[m+1];
		for(int i=1;i<=n;i++) {
			x.nextToken();
			left[i]=(int)x.nval;
		}
		for(int i=1;i<=m;i++) {
			x.nextToken();
			right[i]=(int)x.nval;
		}
		double dp[][][]=new double[n+1][m+1][2];
		double pd=(double)l/2;
		double a=js(0,left[1],pd);
		double b=js(0,right[1],pd);
		for(int i=0;i<=n;i++)//初始化，全部置为最大
			for(int j=0;j<=m;j++)
				Arrays.fill(dp[i][j], INF);
		dp[1][0][0]=a;
		dp[0][1][1]=b;
		/*for(int i=1;i<=n;i++) {
			dp[i][0][0]=a+left[i]-left[1];
			dp[i][0][1]=INF;
		}
		for(int i=1;i<=m;i++) {
			dp[0][i][0]=INF;
			dp[0][i][1]=b+right[i]-right[1];
		}*/
		for(int i=0;i<=n;i++) {
			for(int j=0;j<=m;j++) {
				if(i!=0)dp[i][j][0]=Math.min(dp[i][j][0],Math.min(dp[i-1][j][0]+left[i]-left[i-1], dp[i-1][j][1]+js(left[i],right[j],l)));
				if(j!=0)dp[i][j][1]=Math.min(dp[i][j][1],Math.min(dp[i][j-1][0]+js(left[i],right[j],l), dp[i][j-1][1]+right[j]-right[j-1]));
			}
		}
		out.printf("%.2f\n", Math.min(dp[n][m][0]+js(k,left[n],pd), dp[n][m][1]+js(k,right[m],pd)));//最后还要到达画廊中间别忘了
		out.flush();
	}
	public static double js(double a,double b,double h) {
		a=Math.abs(a-b);
		return Math.sqrt(a*a+h*h);
	}
}