题目

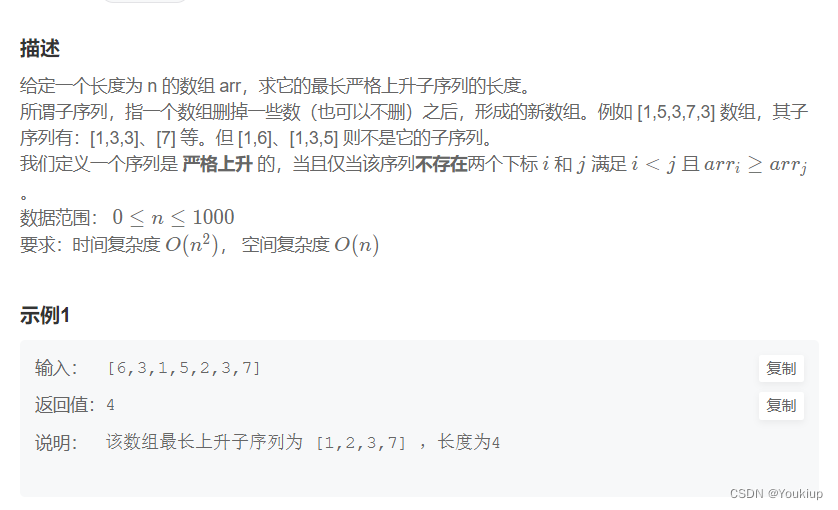
BM71 最长上升子序列(一)

分析

dp[i] 考虑到下标i，其组成的最长上升子序列长度

可以用动态规划的原因： 到i的结果可以由到j （j<i) 的结果推出，只需要判断下标j对应的数字是否比下标i 对应的字母小即可

注意：要特判数组为空的情况

状态转移：dp[i] = max(dp[j] + 1,dp[i])

代码

class Solution:
    def LIS(self , arr: List[int]) -> int:
        # write code here
        n = len(arr)
        # 特判数组为空的情况 0<=n
        if n == 0:
            return 0
        # dp[i] 考虑到下表为i的数组，其最长上升子序列长度，初始化为1，至少有一个字母
        dp = [1 for i in range(n)]
        # 考虑到下标为i
        for i in range(n):
            # 考虑i前面的升序元素
            for j in range(i):
                if arr[j]<arr[i]:
                    dp[i] = max(dp[j] + 1,dp[i])
        return max(dp)