栈

栈的概述

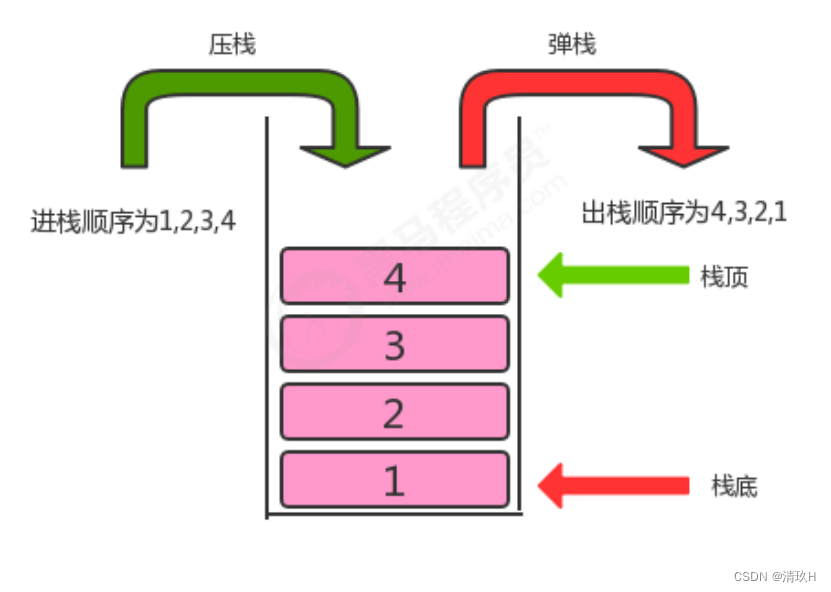
栈是一种基于先进后出(FILO)的数据结构，是一种只能在一端进行插入和删除操作的特殊线性表。它按照先进后出
的原则存储数据，先进入的数据被压入栈底，最后的数据在栈顶，需要读数据的时候从栈顶开始弹出数据（最后一
个数据被第一个读出来）。
我们称数据进入到栈的动作为压栈，数据从栈中出去的动作为弹栈。

在这里插入图片描述

栈的实现

栈API设计

在这里插入图片描述

栈代码实现

import java.util.Iterator

public class Stack<T> implements Iterable<T> {
	//记录首结点
	private Node head;
	//栈中元素的个数
	private int N;

	public Stack() {
		head = new Node(null, null);
		N = 0;
	}

	//判断当前元素个数是否为0
	public boolean isEmpty() {
		return N == 0;
	}

	//把t元素压入栈
	public void push(T t) {
		Node oldNext = head.next;
		head.next = node;
		//个数+1
		N++;
	}

	//弹出栈顶元素
	public T pop() {
		Node oldNext = head.next;

		if(oldNext == null) {
			return null;
		}
		//删除首个元素
		head.next = head.next.next;
		//个数-1
		N--;
		return oldNext.item;
	}

	//获取栈中元素的个数
	public int size() {
		return N;
	}

	@Override
	public Iterator<T> iterator() {
		return new SIterator();
	}
	
	private class SIterator implements Iterator<T> {
		private Node n = head;
		@Override
		public boolean hasNext() {
			return n.next!=null;
		}
		@Override
		public T next() {
			Node node = n.next;
			n = n.next;
			return node.item;
		}
	}
	
	private class Node{
		public T item;
		public Node next;
		public Node(T item, Node next) {
			this.item = item;
			this.next = next;
		}
	}
}

栈的应用

栈在系统中的应用

编译器在词法分析的过程中处理括号、花括号等这个符号的逻辑，就是使用了栈这种数据结构。

递归的实现是栈：每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中，然后递归返回的时候，从栈顶弹出上一次递归的各项参数，所以这就是递归为什么可以返回上一层位置的原因。

所以栈在计算机领域中应用是非常广泛的。

括号匹配问题

括号匹配是使用栈解决的经典问题。对应于力扣上的题目有效的括号

建议要写代码之前要分析好有哪几种不匹配的情况，如果不动手之前分析好，写出的代码也会有很多问题。

先来分析一下这里有三种不匹配的情况，

第一种情况，字符串里左方向的括号多余了，所以不匹配。
第二种情况，括号没有多余，但是括号的类型没有匹配上。
第三种情况，字符串里右方向的括号多余了，所以不匹配。
这里还有一些技巧，在匹配左括号的时候，右括号先入栈，就只需要比较当前元素和栈顶相不相等就可以了，比左括号先入栈代码实现要简单的多了！

字符串去重问题

对应于力扣上的题目删除字符串中的所有相邻重复项

思路就是可以把字符串顺序放到一个栈中，然后如果相同的话栈就弹出，这样最后栈里剩下的元素都是相邻不相同的元素了

逆波兰表达式问题

逆波兰表达式求值问题是我们计算机中经常遇到的一类问题，要研究明白这个问题，首先我们得搞清楚什么是逆波兰表达式？要搞清楚逆波兰表达式，我们得从中缀表达式说起。

中缀表达式

中缀表达式就是我们平常生活中使用的表达式，例如：1+3*2,2-(1+3)等等，中缀表达式的特点是：二元运算符总是置于两个操作数中间。

中缀表达式是人们最喜欢的表达式方式，因为简单，易懂。但是对于计算机来说就不是这样了，因为中缀表达式的运算顺序不具有规律性。不同的运算符具有不同的优先级，如果计算机执行中缀表达式，需要解析表达式语义，做大量的优先级相关操作。

逆波兰表达式(后缀表达式)

后缀表达式的特点：运算符总是放在跟它相关的操作数之后

在这里插入图片描述
关于中缀表达式转后缀表达式的实现以及后缀表达式计算结果的具体实现：栈的应用-四则运算表达式求值

题目的代码实现请查看20. 有效的括号、1047. 删除字符串中的所有相邻重复项、150. 逆波兰表达式求值

队列

队列的概述

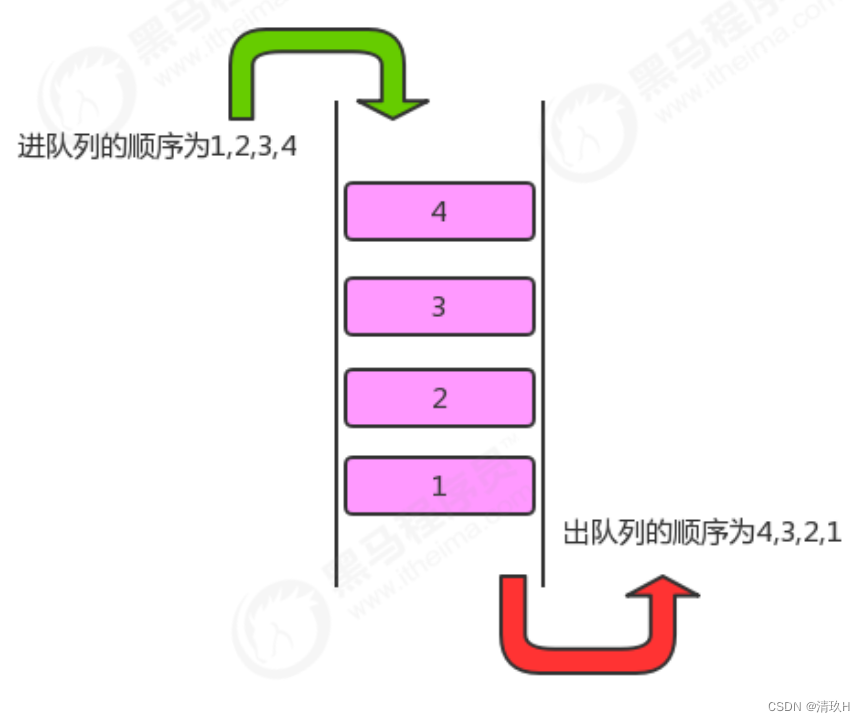
队列是一种基于先进先出(FIFO)的数据结构，是一种只能在一端进行插入,在另一端进行删除操作的特殊线性表，它按照先进先出的原则存储数据，先进入的数据，在读取数据时先读被读出来。

在这里插入图片描述

队列的实现

队列的API设计

在这里插入图片描述

队列代码实现

import java.util.Iterator;

public class Queue<T> implements Iterable<T>{
	//记录首结点
	private Node head;
	//记录最后一个结点
	private Node last;
	//记录队列中元素的个数
	private int N;
	public Queue() {
		head = new Node(null,null);
		last=null;
		N=0;
	}
	//判断队列是否为空
	public boolean isEmpty(){
		return N==0;
	}
	//返回队列中元素的个数
	public int size(){
		return N;
	}
	//向队列中插入元素t
	public void enqueue(T t){
		if (last==null){
			last = new Node(t,null);
			head.next=last;
		}else{
			Node oldLast = last;
			last = new Node(t,null);
			oldLast.next=last;
		}
		//个数+1
		N++;
	}
	//从队列中拿出一个元素
	public T dequeue(){
		if (isEmpty()){
			return null;
		}
		Node oldFirst = head.next;
		head.next = oldFirst.next;
		N--;
		if (isEmpty()){
			last=null;
		}
		return oldFirst.item;
	}
	
	@Override
	public Iterator<T> iterator() {
		return new QIterator();
	}
	
	private class QIterator implements Iterator<T>{
		private Node n = head;
		@Override
		public boolean hasNext() {
			return n.next!=null;
		}
		@Override
		public T next() {
			Node node = n.next;
			n = n.next;
			return node.item;
		}
	}
	
	private class Node{
		public T item;
		public Node next;
		public Node(T item, Node next) {
			this.item = item;
			this.next = next;
		}
	}
}

队列的经典题目

滑动窗口最大值问题

对应的是力扣中的题目滑动窗口最大值

主要思想是队列没有必要维护窗口里的所有元素，只需要维护有可能成为窗口里最大值的元素就可以了，同时保证队列里的元素数值是由大到小的。

那么这个维护元素单调递减的队列就叫做单调队列，即单调递减或单调递增的队列。java中没有直接支持单调队列，需要我们自己来一个单调队列

而且不要以为实现的单调队列就是对窗口里面的数进行排序，如果排序的话，那和优先级队列又有什么区别了呢。

设计单调队列的时候，pop，和push操作要保持如下规则：

pop(value)：如果窗口移除的元素value等于单调队列的出口元素，那么队列弹出元素，否则不用任何操作
push(value)：如果push的元素value大于入口元素的数值，那么就将队列出口的元素弹出，直到push元素的数值小于等于队列入口元素的数值为止
保持如上规则，每次窗口移动的时候，只要问que.front()就可以返回当前窗口的最大值。

首先要明确的是，题解中单调队列里的pop和push接口，仅适用于本题。

单调队列不是一成不变的，而是不同场景不同写法，总之要保证队列里单调递减或递增的原则，所以叫做单调队列。