欢迎浏览高耳机的博客

希望我们彼此都有更好的收获

感谢三连支持！

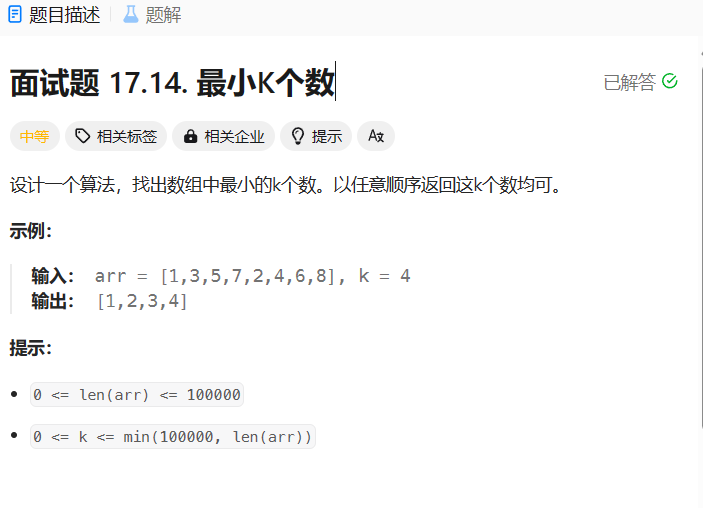
首先我们会想到，通过建立小根堆，使堆顶元素为数组中的最小元素；

然后使堆顶元素出堆，循环K次；

 public int[] smallestK2(int[] arr, int k){
        int[] tmp = new int[k];
        if(k == 0){
            return tmp;
        }
        PriorityQueue<Integer> minHeap = new PriorityQueue();
        for (int i = 0; i < arr.length; i++) {
            minHeap.push(arr[i]);
//O(n * logn)
        }
        for (int i = 0; i < k; i++) {
            tmp[i] = minHeap.pollHeap();
//O(k * logn)
        }
        return tmp;
    }

但该解法只是PriorityQueue的简单使用，并不是topK最好的做法；

这个算法的时间复杂度可以分为几个部分来看：

1. 将数组元素插入优先队列（最小堆）的时间复杂度为 O(n * log(n))，其中 n 为数组的长度 arr.length。
2. 从优先队列中弹出 k 个最小元素的时间复杂度为 O(k * log(n))，因为每次弹出最小元素的操作的时间复杂度是 O(log(n))。

因此，总的时间复杂度为 O(n * log(n) + k * log(n))。如果 k 远小于 n，那么算法的时间复杂度可以近似为 O(n * log(n))。并不是最理想的方法；

---

我们可以先将数组前K个元素建立大根堆（没错，是大根堆！），再接着遍历剩下N-K个元素；

如果当前堆顶的元素大于遍历的数组元素，则说明堆顶元素不是前K个最小元素之一；

此时将堆顶元素出堆，遍历到的数组元素入堆，最终堆中就是要求的前K个最小元素；

class IntCmp implements Comparator<Integer> {

    @Override
    public int compare(Integer o1, Integer o2) {
        return o2.compareTo(o1);
    }
//此接口将默认的建立小根堆改为建立大根堆；
}

public class PriorityQueue {

    public int[] smallestK1(int[] arr, int k) {
        int[] tmp = new int[k];
        if(k == 0){
            return tmp;
        }
        PriorityQueue<Integer> minHeap = new PriorityQueue<>(new IntCmp());
        //1.把前k个元素放进堆中;
        for (int i = 0; i < k; i++) {
            minHeap.push(arr[i]);
        }
        //2.遍历剩下N - K个元素;
        for (int i = k; i < arr.length; i++) {
            int val = minHeap.peekHeap();
            if(val > arr[i]){
                minHeap.pollHeap();
                minHeap.push(arr[i]);
            }
        }
        //3.将遍历好的大堆放入数组，此时数组都是为最小元素;
        for (int i = 0; i < k; i++) {
            tmp[i] = minHeap.pollHeap();
        }
        return tmp;
    }

这个算法的实践复杂度可以通过对每个步骤的操作进行分析得出：

1. 将前 k 个元素放入最小堆中的操作需要 O(k * log(k)) 的时间，因为每次插入元素的时间复杂度为 O(log(k))。
2. 遍历剩下的 N - K 个元素并进行堆的调整，最坏情况下需要遍历 N - K 个元素，并在每个元素需要更新堆时执行插入和弹出操作，每个操作的时间复杂度均为 O(log(k))。因此，遍历和调整的总时间复杂度为 O((N - K) * log(k))。
3. 最后将堆中的元素放入数组中的操作需要 O(k * log(k)) 的时间。

因此，整个算法的时间复杂度为 O((N - K) * log(k) + k * log(k))，其中 N 为数组的长度 arr.length，k 为要求的最小元素个数。如果 k 远小于 n，那么算法的时间复杂度可以近似为 O((N-K) * log(K))。较前一种方法来看更为理想。

---

希望这篇博客能为你理解java编程思想提供一些帮助。

如有不足之处请多多指出。

我是高耳机。