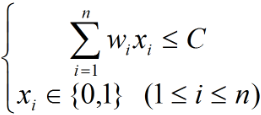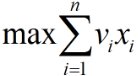目录
一、前言
二、DP概念
1、最少硬币问题
2、DP的两个特征
三、0/1背包(最经典的DP问题)
1、小明的背包1(lanqiaoOJ题号1174)
2、空间优化:滚动数组
1)交替滚动
2)自我滚动
一、前言
本文讲解了DP的基础概念和一道DP(01背包)例题,介绍了滚动数组的优化。
二、DP概念
1、最少硬币问题
【回顾贪心解法】
硬币面值1、2、5。支付13元,要求硬币数量最少。
贪心:1)5元硬币,2个
2)2元硬币,1个
3)1元硬币,1个
硬币面值 1、2、4、5、6。支付9元。
贪心:1)6元硬币,1个
2)2元硬币,1个
3)1元硬币,1个。
错误!
答案是:5元硬币+4元硬币=2个
硬币问题的正解是动态规划。
type = [1, 5, 10, 25, 50] #5种面值
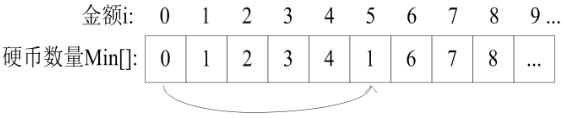
定义数组 Min[] 记录最少硬币数量:
对输入的某个金额 i,Min[i] 是最少的硬币数量。
第一步:只考虑1元面值的硬币金额
i=1元时,等价于:
(i=i-1=0) 元需要的硬币数量+1个1元硬币
把 Min[] 叫做 “状态”
把 Min[] 的变化叫做 “状态转移”
继续,所有金额仍然都只用1元硬币
i=2元时,等价于:(i=i-1=1)元需要的硬币数量,加上1个1元硬币。
i=3元时…..
i=4元时.....
在1元硬币的计算结果基础上,再考虑加上5元硬币的情况。从i=5开始就行了:
i=5元时,等价于:
1) i=i-5=0 元需要的硬币数量,加上1个5元硬币。Min[5]=1。
2)原来的 Min[5]=5。
取 (1)、(2) 的最小值,所以 Min[5]=1。
i=6元时,等价于:
1)i=i-5=1 元需要的硬币数量,加上1个5元硬币。Min[6]=2
2)原来的 Min[6]=6
取 (1) (2) 的最小值,所以 Min[6]=2
i=7元时,…
i=8元时,…
用1元和5元硬币,结果:
递推关系:(状态转移方程)
Min[i] = min(Min[i], Min[i-5]+1)
继续处理其它面值硬币。
def solve(s):
Min=[int(1e12)]*(s+1) #初始化为无穷大
Min[0]=0
for j in range(cnt): #5种硬币
for i in range(money[j],s+1):
Min[i]=min(Min[i],Min[i-money[j]]+1)
print(Min[s])
cnt=5 #5种面值
money=[1,5,10,25,50] #面值可换
s=int(input())
solve(s)
注意:我们习惯把状态命名为 dp[],即上面代码的 Min 改为 dp。
2、DP的两个特征
1)重叠子问题。子问题是原大问题的小版本,计算步骤完全一样;计算大问题的时候,需要多次重复计算小问题。
一个子问题的多次计算,耗费了大量时间。用DP处理重叠子问题,每个子问题只需要计算一次,从而避免了重复计算,这就是DP效率高的原因。
2)最优子结构。首先,大问题的最优解包含小问题的最优解;其次,可以通过小问题的最优解推导出大问题的最优解。
补充:
1)记忆化
- 如果各个子问题不是独立的,如果能够保存已经解决的子问题的答案,在需要的时候再找出已求得的答案,可以避免大量的重复计算。
- 基本思路:用一个表记录所有已解决的子问题的答案,不管该问题以后是否被用到,只要它被计算过,就将其结果填入表中。
- 这就是记忆化。
2)求解过程
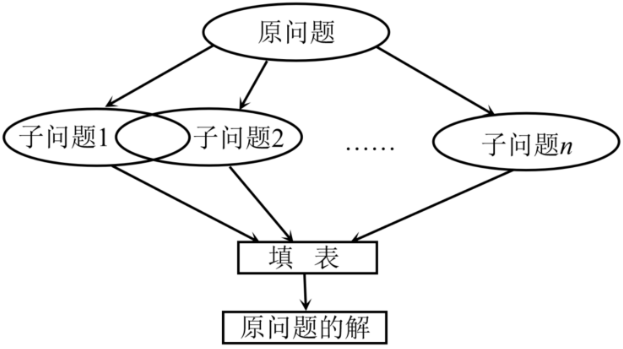
三、0/1背包(最经典的DP问题)
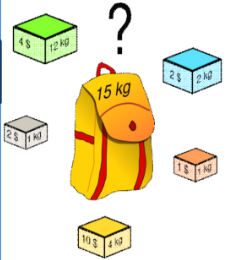
- 给定 n 种物品和一个背包,物品 i 的重量是 wi,其价值为 vi,背包的容量为 C。
- 背包问题:选择装入背包的物品,使得装入背包中物品的总价值最大
- 如果在选择装入背包的物品时,对每种物品 i 只有两种选择:装入背包或不装入背包,称为0/1背包问题。
- 设 xi 表示物品 i 装入背包的情况:
xi=0,表示物品 i 没有被装入背包
xi=1,表示物品 i 被装入背包
- 约束条件:
- 目标函数:
【举例子】
例:有 5 个物品,重量分别是 {2, 2, 6, 5, 4},价值分别为 {6, 3, 5, 4, 6},背包的容量为10。
定义一个 (n+1)×(C+1) 的二维表 dp[][]
表示把前 i 个物品装入容量为 j 的背包中获得的最大价值。

填表:按只放第 1 个物品、只放前 2 个、只放前 3 个 …...一直到放完,这样的顺序考虑。(从小问题扩展到大问题)
1、只装第1个物品。(横向是递增的背包容量)
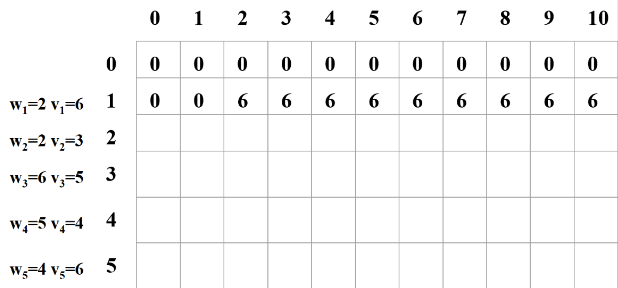
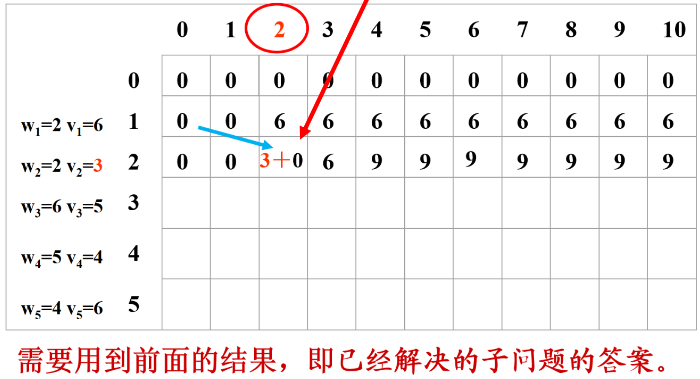
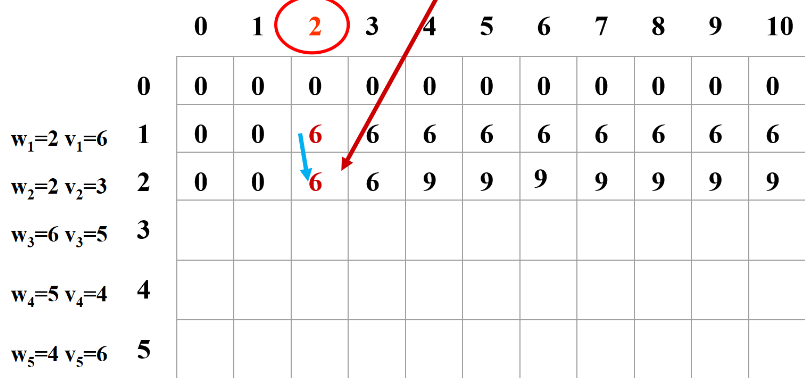
2、只装前2个物品。
如果第 2 个物品重量比背包容量大,那么不能装第2个物品,情况和只装第 1 个一样。
如果第 2 个物品重量小于背包容量,那么:
1)如果把物品 2 装进去 (重量是2),那么相当于只把 1 装到 (容量-2) 的背包中。
2)如果不装 2, 那么相当于只把 1 装到背包中。
一一取(1)和(2)的最大值。
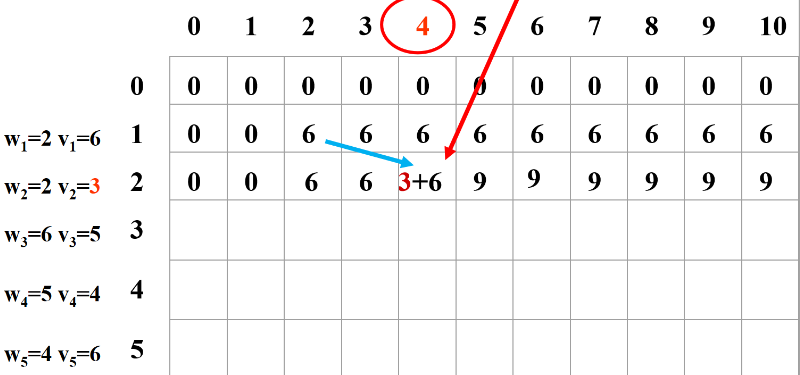
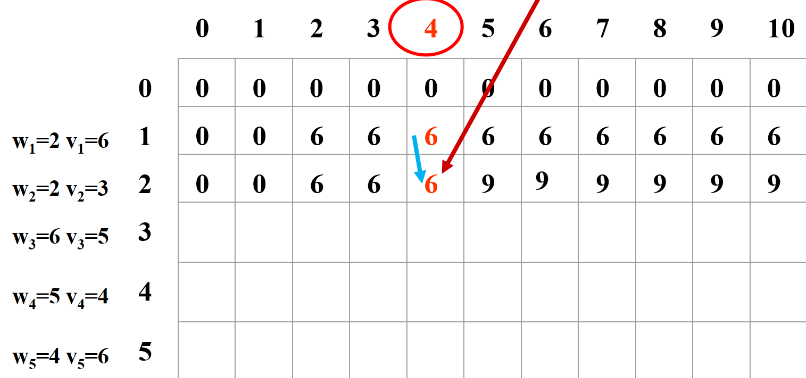
接着继续更新表格。
1)如果把物品 2 装进去 (重量是2),那么相当于只把 1 装到 (容量-2) 的背包中。
2)如果不装 2, 那么相当于只把 1 装到背包中。
一一取(1)和(2)的最大值。
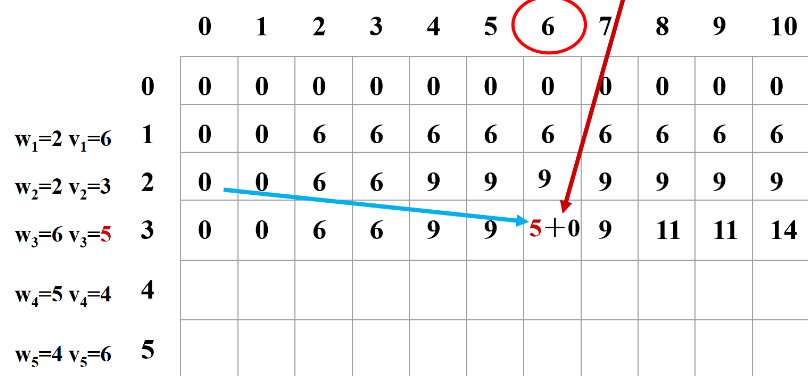
3、只装前3个物品。
如果第 3 个物品重量比背包大,那么不能装第 3 个物品,情况和只装第1、2个一样。
如果第 3 个物品重量小于背包容量,那么:
1)如果把物品 3 装进去(重量是6),那么相当于只把 1、2 装到 (容量-6) 的背包中。
2)如果不装 3,那么相当于只把 1、2 装到背包中。——取(1)和(2)的最大值。
按这样的规律一行行填表,直到结束。现在回头考虑,装了哪些物品。
看最后一列,15>14,说明装了物品 5,否则价值不会变化。
DP复杂度?可以先自己想一想。
1、小明的背包1(lanqiaoOJ题号1174)
【题目描述】
小明有一个容量为 C 的背包。这天他去商场购物,商场一共有 N 件物品,第 i 件物品的体积为 ci,价值为 wi。小明想知道在购买的物品总体积不超过 C 的情况下所能获得的最大价值为多少,请你帮他算算。
【输入描述】
输入第 1 行包含两个正整数 N, C,表示商场物品的数量和小明的背包容量。第 2~N+1 行包含 2 个正整数 c, w,表示物品的体积和价值。1<=N<=10^2,1<=C<=10^3,1<=wi,ci<=10^3。
【输出描述】
输出一行整数表示小明所能获得的最大价值。
- DP状态:定义二维数组dp[][],大小为 N×C。
- dp[i][j]:把前 i 个物品 (从第1个到第i个) 装入容量为 j 的背包中获得的最大价值。
- 把每个 dp[i][j] 看成一个背包:背包容量为 j,装 1~i 这些物品。最后得到的 dp[N][C] 就是问题的答案:把 N个物品装进容量 C 的背包的最大价值。
【下面的分析是精髓⭐⭐⭐⭐⭐】
递推计算到 dp[i][j],分 2 种情况:
1)第 i 个物品的体积比容量 j 还大,不能装进容量 j 的背包。那么直接继承前 i-1 个物品装进容量 j 的背包的情况即可:dp[i][j] = dp[i-1][j]。
2)第 i 个物品的体积比容量 j 小,能装进背包。又可以分为 2 种情况:装或者不装第 i 个。
①装第 i 个。从前 i-1 个物品的情况下推广而来,前 i-1 个物品是 dp[i-1][j]。第 i 个物品装进背包后,背包容量减少 c[i],价值增加 w[i]。有:dp[i][j] = dp[i-1][j-c[i]] + w[i]。
②不装第 i 个。那么:dp[i][j] = dp[i-1][j]。
取①和②的最大值,状态转移方程:
dp[i][j] = max(dp[i-1][j], dp[i-1][j-c[i]] +w[i])
def solve(n,C):
for i in range(1,n+1):
for j in range(0,C+1):
if c[i]>j:
dp[i][j]=dp[i-1][j]
else:
dp[i][j]=max(dp[i-1][j],dp[i-1][j-c[i]]+w[i])
return dp[n][C]
N=3011
dp=[[0]*N for i in range(N)]
w=[0]*N
c=[0]*N
n,C=map(int,input().split())
for i in range(1,n+1):
c[i],w[i]=map(int,input().split())
print(solve(n,C))2、空间优化:滚动数组
把 dp[][] 优化成一维的 dp[],以节省空间。
dp[i][] 是从上面一行 dp[i-1] 算出来的,第 i 行只跟第 i-1 行有关系,跟更前面的行没有关系:
dp[i][i] = max(dp[i - 1][i], dp[i -1][i - c[i]] + w[i])
优化:只需要两行 dp[0][]、dp[1][],用新的一行覆盖原来的一行,交替滚动。
经过优化,空间复杂度从 O(N×C) 减少为 O(C)。
1)交替滚动
定义dp[2][i]:用 dp[0][] 和 dp[1][] 交替滚动。
优点:逻辑清晰、编码不易出错,建议初学者采用这个方法。
now 始终指向正在计算的最新的一行,old 指向已计算过的旧的一行。
对照原递推代码, now 相当于 i,old 相当于 i-1。
def solve(n,C):
old=1
now=0
for i in range(1,n+1):
old,now=now,old
for j in range(0,C+1):
if c[i]>j:
dp[now][j]=dp[old][j]
else:
dp[now][j]=max(dp[old][j],dp[old][j-c[i]]+w[i])
return dp[now][C]
N=3011
dp=[[0]*N for i in range(2)]
w=[0]*N
c=[0]*N
n,C=map(int,input().split())
for i in range(1,n+1):
c[i],w[i]=map(int,input().split())
print(solve(n,C))
2)自我滚动
继续精简:用一个一维的 dp[] 就够了,自己滚动自己。
def solve(n,C):
for i in range(1,n+1):
for j in range(C,c[i]-1,-1):
dp[j]=max(dp[j],dp[j-c[i]]+w[i])
return dp[C]
N=3011
dp=[0]*N
w=[0]*N
c=[0]*N
n,C=map(int,input().split())
for i in range(1,n+1):
c[i],w[i]=map(int,input().split())
print(solve(n,C))
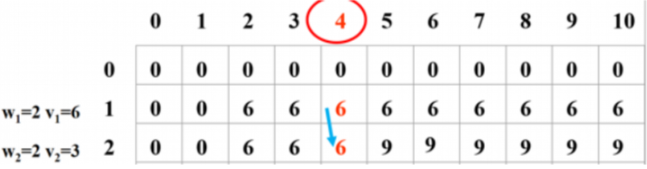
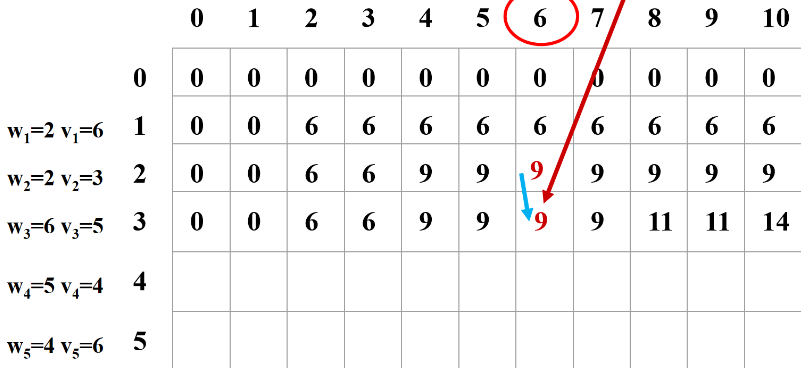
注意:j 从小往大循环是错误的
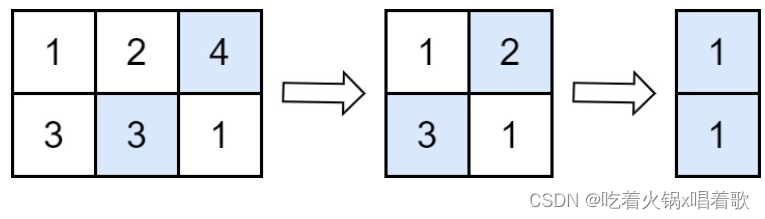
例如 i = 2 时,左图的 dp[5] 经计算得到 dp[5] = 9,把 dp[5] 更新为 9。
右图中继续往后计算,当计算 dp[8] 时,得 dp[8] = dp[5]' + 3 = 9+3 = 12,这个答案是错的。
错误的产生是滚动数组重复使用同一个空间引起的。

而从大到小是对的。

以上,DP初入门
祝好