目录
1.判断题
1-1
1-2
1-3
1-4
2.选择题
2-1
2-2
2-3
3.多选题
3-1
4.填空题
4-1
4-2
4-3
4-4
4-5
5.主观题
5-1
5-2
5-3
5-4
1.判断题
1-1
ϕ⊆{ϕ} (对)
1-2
{a,b}∈{a,b,c,{a,b}} (对)
1-3
{a,b}∈{a,b,c,{{a,b}}} (错)
1-4
若f : A→B既是满射又是单射的,则称f : A→B是双射函数。所以f : R→R,f(x)=2x+1是双射函数。(对)
2.选择题
2-1
下列说法错误的是( D )。
A.
对于A上的任何关系R1和R2都有R10=R20=R。
B.
设A,B,C是任意集合,若A≈B,B≈C,则A≈C。
C.
任何公式都能等值地化成{¬,→,∧}中的公式,即{¬,→,∧}是联结词完备集。
D.
任何图 (无向或有向) 中,奇度顶点的个数可以是偶数也可以是奇数。
2-2
∩{{1},{1,2},{1,2,3}}的值为( B )。
A. {1,2,3}
B. {1}
C. ϕ
D. 1,2,3
2-3
集合A=1,2,3,A的关系R=<1,1>,<1,2>,<2,1>,<3,2>,
下列选项中,( A )是R的自反闭包s(R)。A.
<1,1>,<1,2>,<2,1>,<3,2>,<2,2>,<3,3>
B.
<1,1>,<1,2>,<2,1>,<3,2>,<2,2>,<2,3>,<3,3>
C.
<1,1>,<1,2>,<2,1>,<3,2>,<2,2>,<2,2>,<3,1>
D.
<1,1>,<1,2>,<2,1>,<3,2>,<2,3>
3.多选题
3-1
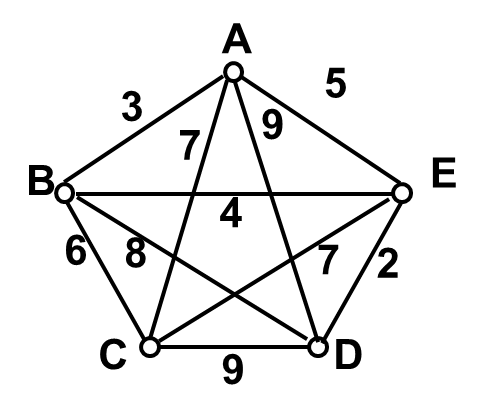
如图所示,下列选项中,说法正确的是( ABCD )。
A. (a)有欧拉回路,是欧拉图,且(a)有哈密顿回路,是哈密顿图
B. (c)有哈密顿回路,是哈密顿图
C. (e)中既没有欧拉回路也没有欧拉通路,但(e)是半哈密顿图
D. (d)是欧拉图,也是哈密顿图
E. (f)是半欧拉图,也是半哈密顿图
4.填空题
4-1
如下图,求出该赋权图的最小生成树,则其W(T)的值为( 15 )
4-2
设R={<1,2>,<1,3>,<2,2>,<2,4>,<3,2>},则
(1)R↾ϕ = ( A ),R[ϕ] = ( A )(从下列A,B选项中选择一项,仅填选项标号,即大写英文字母)。
A. ϕ B. {ϕ}
(2)R↾{2,3} = { < 2 ,2 > , < 2 , 4 > , < 3 , 2 > }
4-3
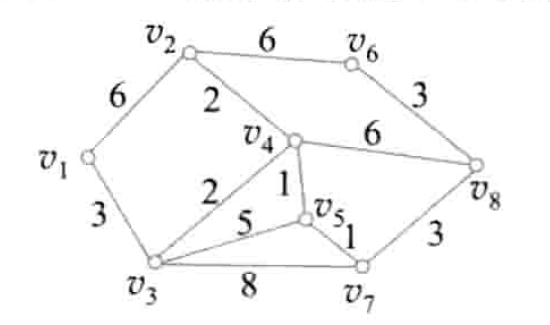
下图为学校各楼的大致分布图,各边权重为楼之间的距离,v1表示宿舍,v2表示2号教学楼,v3表示3号教学楼,v4表示4号教学楼,v5表示图书馆,v6表示体育馆,v7表示医务室,v8表示食堂。
假设一名学生需要在校内各楼栋之间穿梭,需要寻找一条最短的路径,请回答下列问题:
(1)上图中v1到v2的最短路径为:v1,v2 ,距离为 6
(2)上图中v1到v3的最短路径为:v1,v3,v4 ,距离为 3(经过多个点需要以“小写字母v与顶点序号”组合的形式标出,多个顶点之间用英文逗号隔开,参照(1)中的路径填写方式,下同)
(3)上图中v1到v4的最短路径为:v1,v3,v4 ,距离为 5
(4)上图中v1到v5的最短路径为:v1,v3,v4,v5 ,距离为 6
(5)上图中v1到v6的最短路径为:v1,v2,v6 ,距离为 12
(6)上图中v1到v7的最短路径为:v1,v3,v4,v5,v7 ,距离为 7
(7)上图中v1到v8的最短路径为:v1,v3,v4,v5,v7,v8 ,距离为 10
4-4
在自然推理系统P中构造下面推理的证明.
2是素数或合数. 若2是素数,则3 是无理数. 若 3 是无理数,则4不是素数. 所以,如果4是素数,则2是合数.
解:
( 1 )设简单命题
p:2是素数
q:2是合数
r:3 是无理数
s:4是素数( 2 ) 推理的形式结构
前提:p∨q,p→r,r→¬s , 结论:s → q(仅填“p”, “q”, “r”, “s”)( 3 )证明
(仅填“前提引入”、“结论引入”、“置换规则”、“假言推理”、“附加规则”、“化简规则”、“拒取式”、“假言三段论”、“析取三段论”、“构造性二难”、“破坏性二难”、“合取引入”、“结论否定引入”、“附加前提引入”)
例 前提引入①s 附加前提引入
②p → r 前提引入
③r → ¬s 前提引入
④p → ¬s ②③ 假言三段论
⑤¬p ①④ 拒取式
⑥p∨q 前提引入
⑦q ⑤⑥ 析取三段论
4-5
设无向图中有6条边,3度与5度顶点各1个,其余都是2度顶点,那么,该图共有 4 个顶点。(仅填阿拉伯数字)
5.主观题
5-1
设A={0,1,2,3},R为R={ <0,0>,<0,3>,<2,0>,<2,1>,<2,3>,<3,2>}画出R的关系图及关系矩阵MR。
5-2
求出公式(p→q)↔r的主析取范式和主合取范式。
5-3
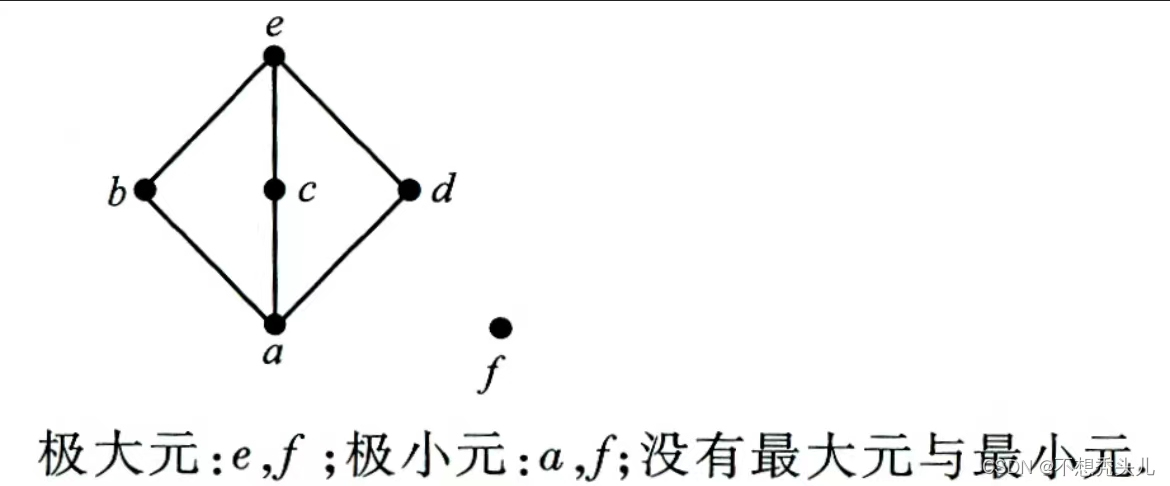
设偏序集<A,R≼>,A=a,b,c,d,e,f,R≼=<a,d>,<a,c>,<a,b>,<a,e>,<b,e>,<c,e>,<d,e>∪IA。请画出该偏序集的哈斯图,并找出A的极大元、极小元、最大元、最小元。
5-4
对24名会外语的科技人员进行掌握外语情况的调查. 其统计结果如下:
会英、日、德和法语的人分别为13,5,10和9人,其中同时会英语和日语的有2人,会英、德和法语中任两种语言的都是4人. 已知会日语的人既不懂法语也不懂德语。
请画出文氏图,分别求只会一种语言 (英、德、法、日) 的人数和会三种语言的人数。


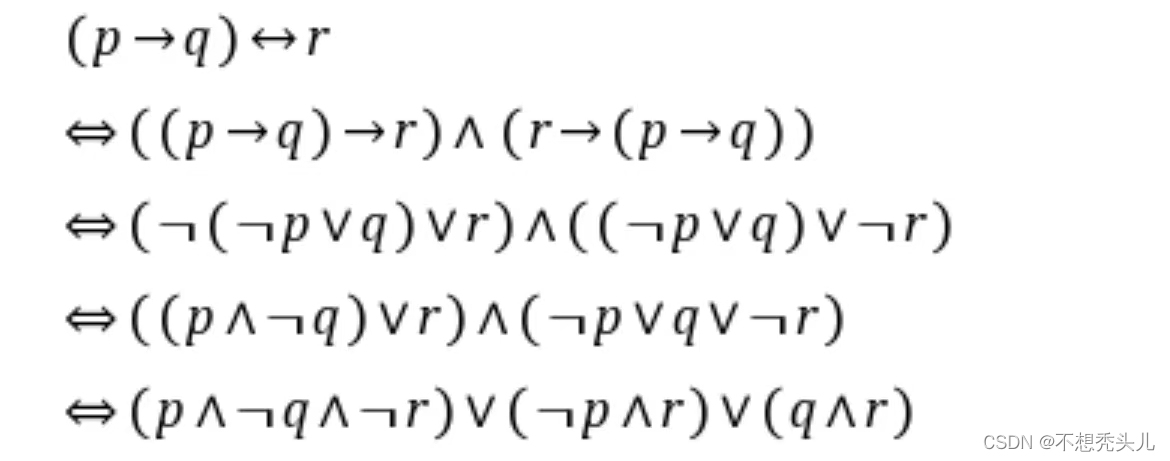


![达梦 执行查询语句时报[-544]:Out of sort buf space](https://img-blog.csdnimg.cn/direct/6b9245c03bab4fd28dc799841c9614eb.png)