💞💞 前言

hello hello~ ，这里是大耳朵土土垚~💖💖 ，欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹

💥个人主页：大耳朵土土垚的博客
💥 所属专栏：数据结构
这里将会不定期更新有关数据结构的内容，希望大家多多点赞关注收藏💖💖

1.建堆的方法

给你一个顺序表或数组（一串数据），通常来说建堆有两种方法一种堆向上调整算法，一种堆向下调整算法建堆也就是筛选法建堆。

筛选法建堆是一种快速建堆的方法，它是在堆排序算法中使用的。这种方法的基本思想是通过不断筛选节点，如果建大堆就将大的节点向上筛选，小的节点向下筛选，小堆就反之，最终得到一个有序的堆。

下面将以将数组int arr[] = {1,8,9,5,3,2}建成一个小堆为例介绍两种方法建堆

2.堆向上调整算法建堆及时间复杂度

✨堆向上调整算法

//向上调整算法
void AdjustUp( int* arr,int child)
{
	//找到双亲节点
	int parent = (child - 1) / 2;
	//向上调整
	while (child > 0)
	{
	//如果父节点大于子节点就交换
		if (arr[parent] > arr[child])
		{
			Swap(&arr[parent], &arr[child]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
			break;

	}
}

因为我们建的是小堆所以父节点肯定是要小于子节点的，所以当遇到父节点大于孩子节点就交换，相应的如果建的是大堆那么父节点小于孩子节点就交换

✨使用堆向上调整算法建堆

堆向上调整算法调整的是最后一个元素，前面的元素必须是一个堆，所以我们在使用堆向上调整算法时可以从一串数的第二个元素开始调整，它前面只有一个元素（一个元素就可以看成一个堆），调整完之后前面两个元素就是一个堆了，再从第三个元素开始调整，依此类推直到最后一个元素

图解如下：
int arr[] = {1,8,9,5,3,2}可以表示为：

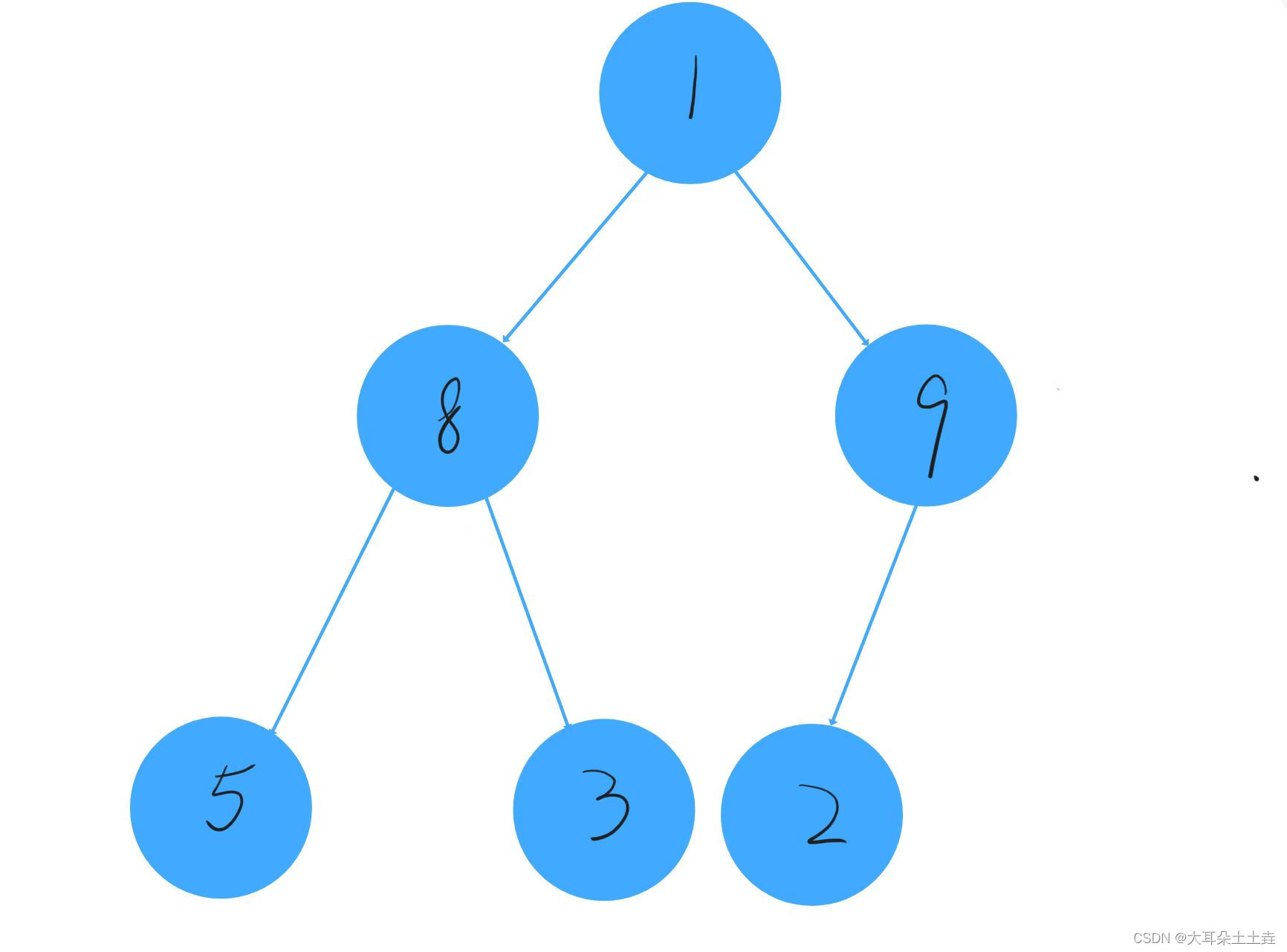
①第一个数据1可以看成一个堆，从第二个节点8开始向上调整，发现1<8，不需要交换：

②前面两个数据1和8已经构成小堆，从第三个元素开始向上调整，发现1<9不需要交换：

③前面三个数据已经构成小堆，从第四个数据5开始向上调整，发现5<8交换,交换后1<5，不需要交换：

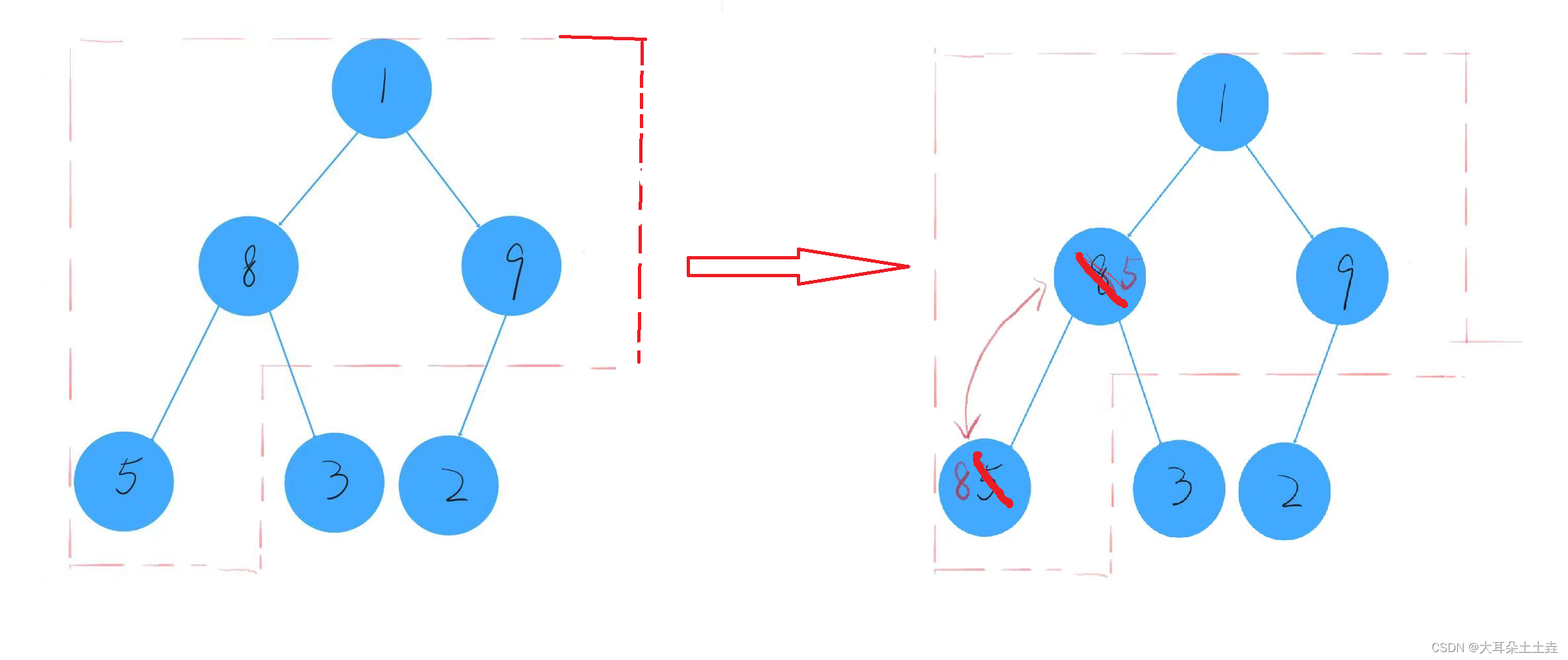
④前面四个数据构成小堆，从第五个数据3开始向上调整建堆，发现3<5交换，1>3不交换：

⑤前面五个数据构成小堆，从第六个数据2开始往上调整建堆，发现2<9交换，1<2不交换：

建好堆之后入下图：

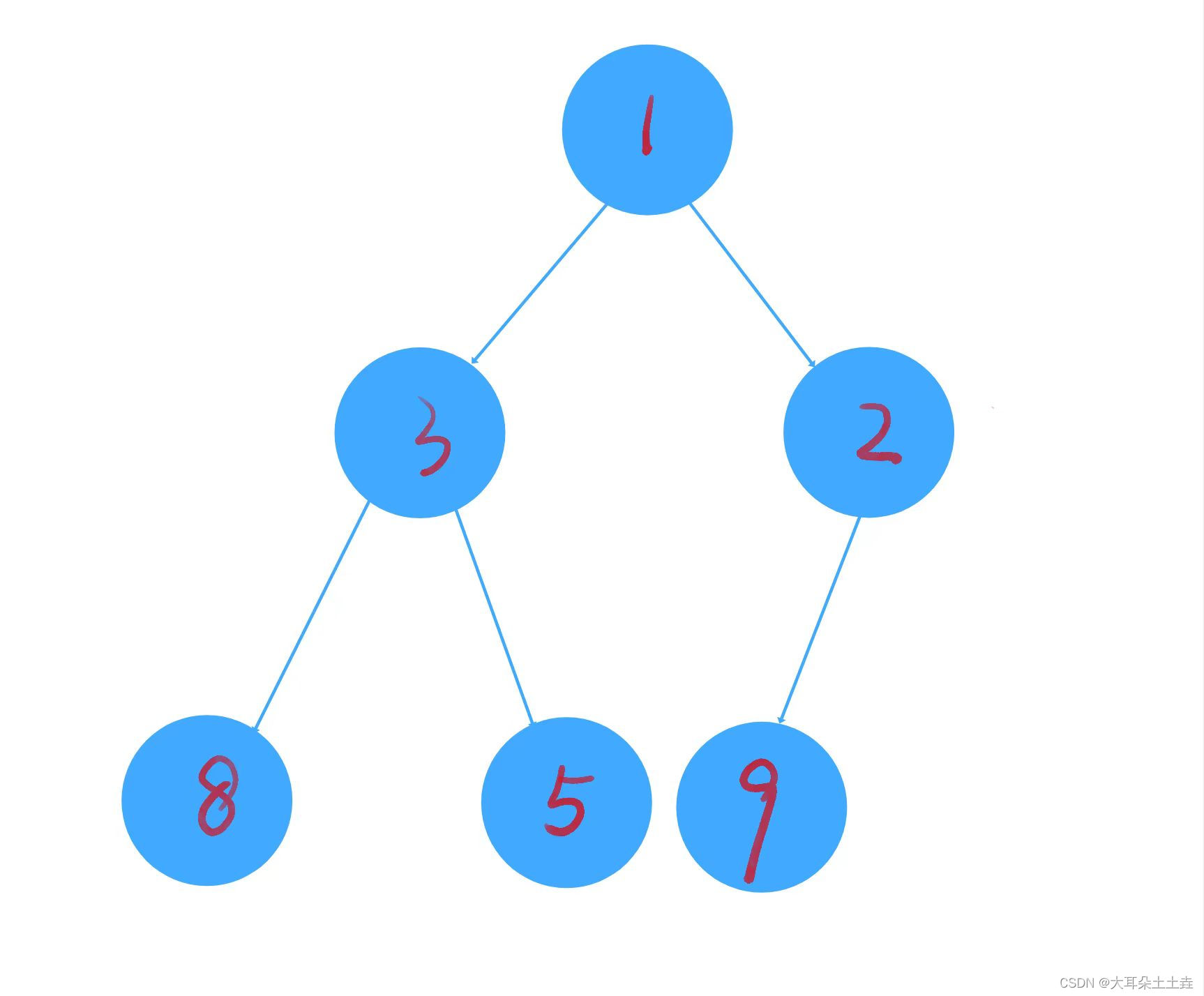
代码如下:

int main()
{
	int arr[] = { 1,8,9,5,3,2};
	//使用堆向上调整算法建堆，需要从第二个节点开始依次往上调整
	for (int i = 1; i < sizeof(arr)/sizeof(int); i++)
	{
		AdjustUp(arr, i);
	}
	//打印数组
	for (int i = 0; i < sizeof(arr)/sizeof(int); i++)
	{
		cout << arr[i] << " ";
	}
	return 0;
}

结果如下：

✨时间复杂度计算

由上图可知，堆向上调整法建堆的时间复杂度是NlogN

logN是以2为底的

3.筛选法建堆及时间复杂度

筛选法建堆需要利用我们的向下调整算法：

✨堆向下调整算法

//堆向下调整算法
void AdjustDown(int* arr,int n, int parent)
{
	//找到较小的孩子节点
	int child = parent * 2 + 1;

	//向下调整
	while (child < n)
	{
		//找到较小的孩子节点
		if (child + 1 < n && arr[child] > arr[child + 1])
		{
			child++;
		}
		//如果父节点大于孩子节点就交换
		if (arr[child] < arr[parent])
		{
			Swap(&arr[child], &arr[parent]);
			parent = child;
			child = child * 2 + 1;
		}
		else
			break;

	}
}

✨使用堆向下调整算法建堆

具体步骤如下：

1. 从完全二叉树中的最后一个非叶子节点开始，将其视为根节点。
2. 从根节点开始，依次向下进行筛选，将当前节点与其左右子节点进行比较，将最大值上移。
3. 完成一次筛选后，将当前节点的上一个节点作为新的根节点，再次进行筛选。
4. 依次类推，直到所有节点都进行过一次筛选，最终得到一个有序的堆。

这里同样要注意，堆向下调整时，其节点左右子树必须是堆，我们从最后一个非叶子节点开始调整是因为其左右子树只有一个数据，可以看成堆

以int arr[] = {1,8,9,5,3,2}为例，图解如下：

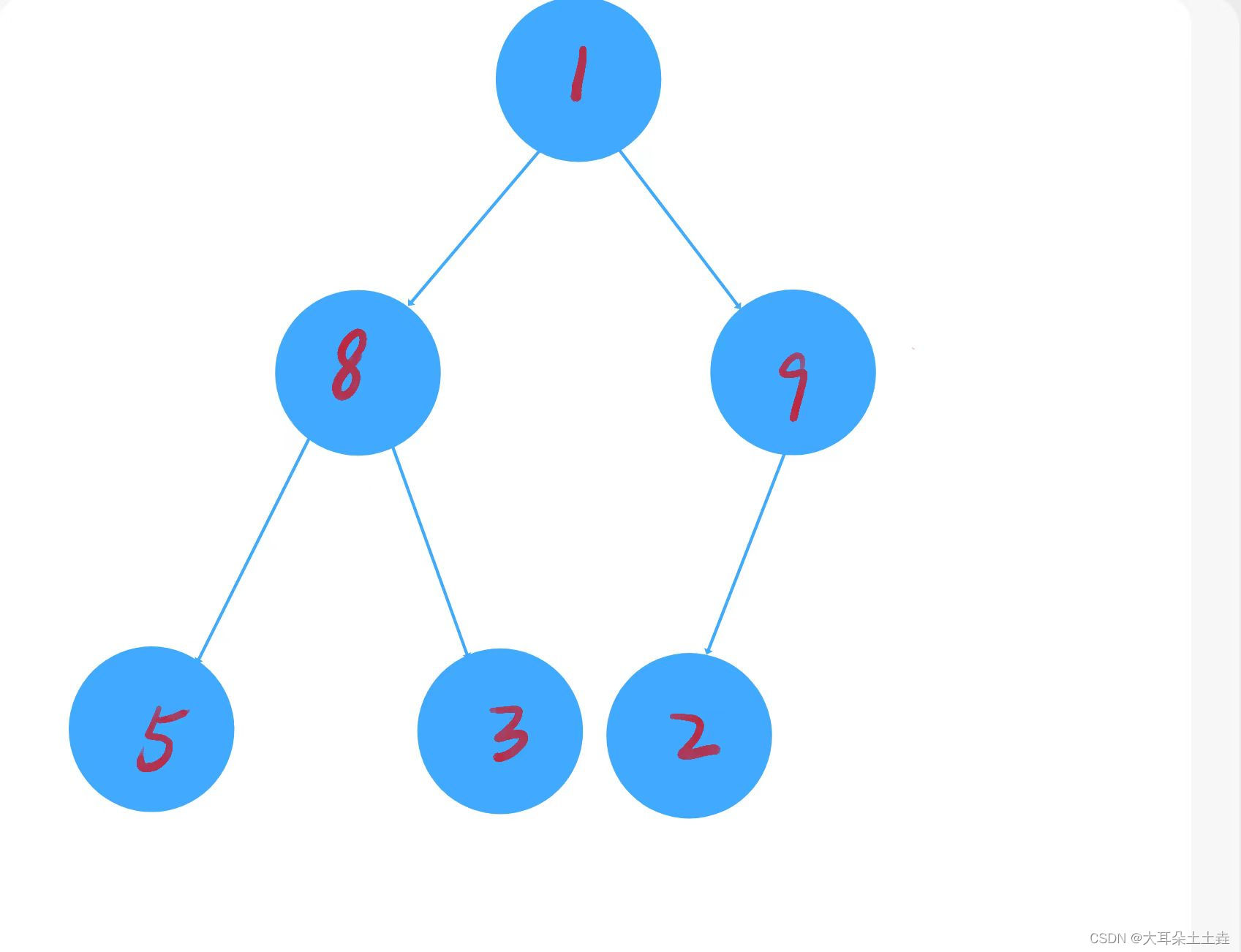
①从最后一个非叶子节点9开始往下调整，发现9>2交换：

②再从上一个节点8开始往下调整，先找到较小的孩子节点3，发现8>3交换：

③再从上一个节点1开始往下调整，找到较小的子节点2，发现1<2不交换：

小堆就建好了：

代码如下：

int main()
{
	int arr[] = { 1,8,9,5,3,2 };
	//使用堆向下调整算法建堆，需要从最后一个非叶子节点开始依次往下调整
	int size = (sizeof(arr) / sizeof(int) - 2) / 2;//找到最后一个非叶子节点下标
	for (int i = size; i >=0; i--)
	{
		AdjustDown(arr, sizeof(arr) / sizeof(int),i);
	}
	//打印数组
	for (int i = 0; i < sizeof(arr) / sizeof(int); i++)
	{
		cout << arr[i] << " ";
	}
	return 0;
}

结果如下：

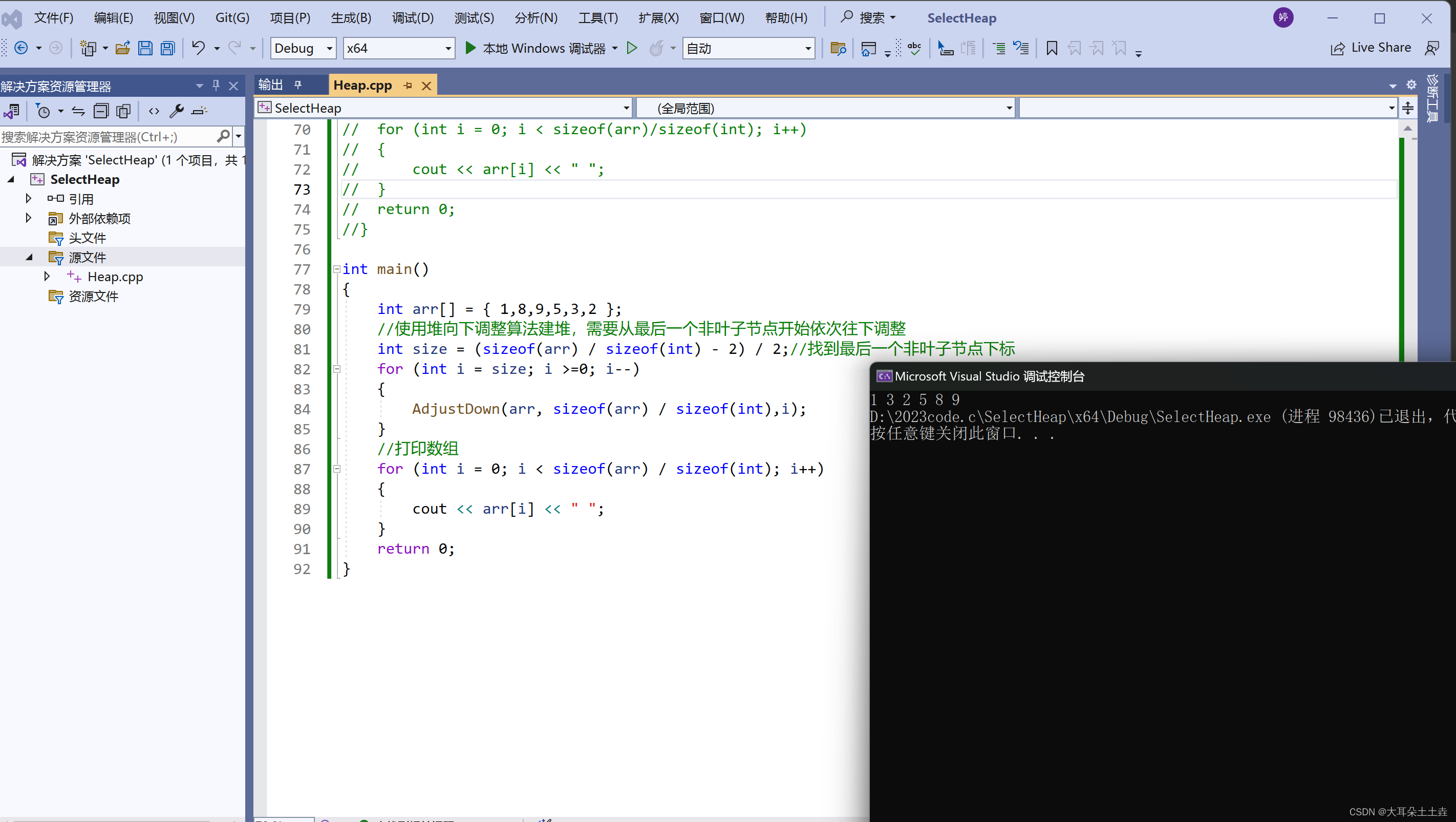
我们发现堆向下调整需要多传一个参数数据个数n，这是因为向下调整时，最坏的情况下会一直向下调整到最后一个节点，此时要控制下标不能越界，所以要传数据个数来防止越界，而前面的向上调整最坏的情况下，会调整到根节点，只需要其下标不小于0就不会越界，所以不需要传参数n

✨时间复杂度计算

由上图可知，堆向下调整法建堆的时间复杂度是N

4.结语

由上述时间复杂度的分析可知，我们最好选用筛选法也就是堆向下调整算法建堆，以上就是今天所有的内容啦~ 完结撒花~ 🥳🎉🎉