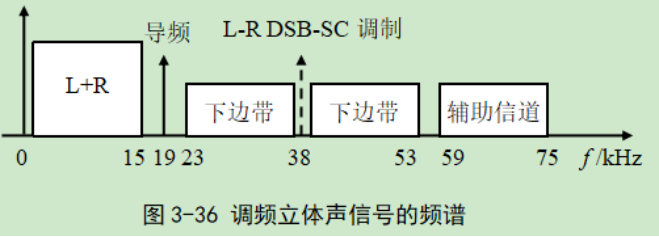
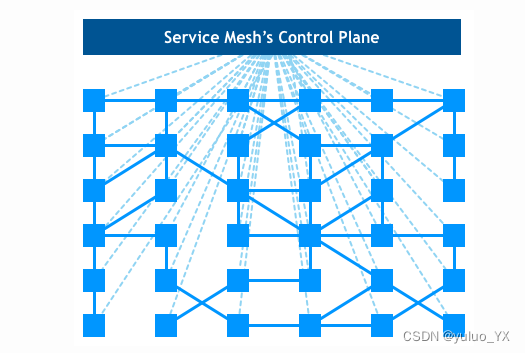
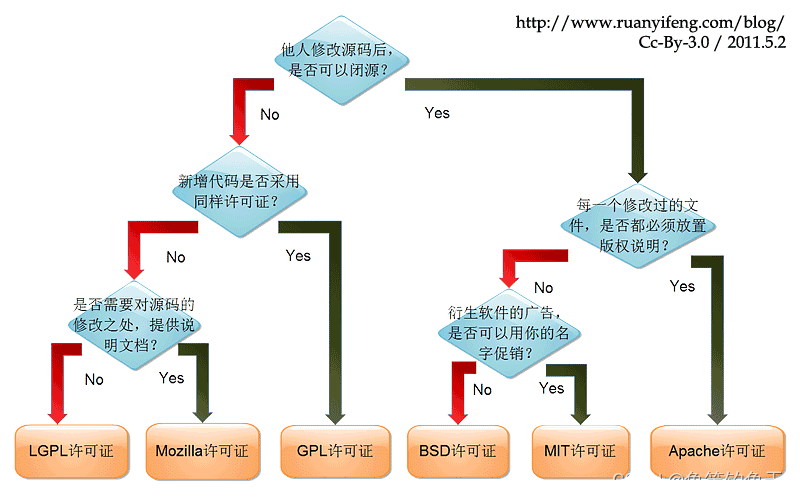
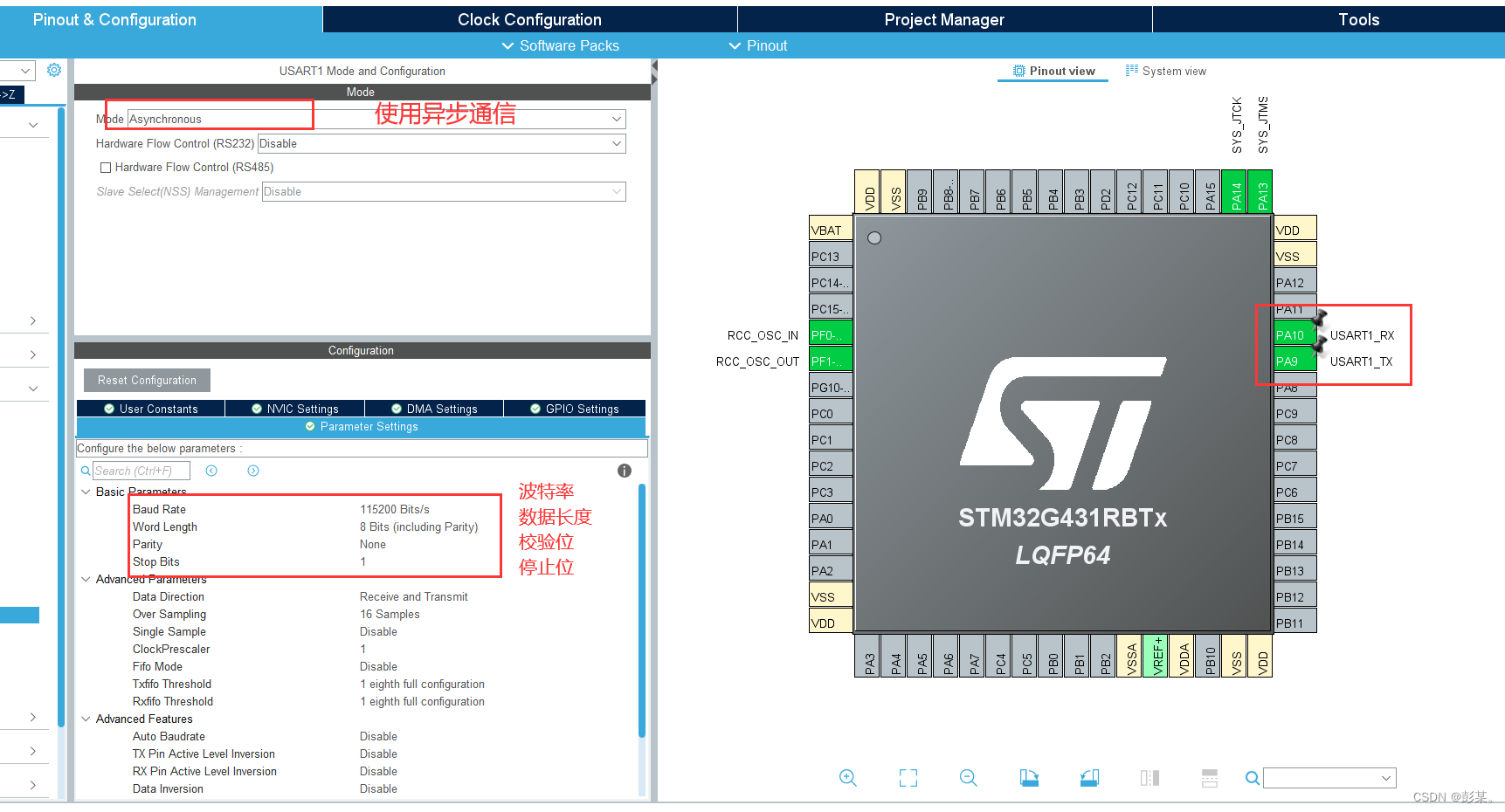
在普通的PID 控制算法中,由于积分系数k是常数,所以在整个控制过程中,积分增量不变。而系统对积分项的要求是,系统偏差大时积分作用应减弱甚至全无,而在偏差小时则应加强。积分系数取大了会产生超调,甚至积分饱和,取小了又迟迟不能消除静差。因此,如何根据系统偏差大小改变积分的速度,对于提高系统品质是很重要的。变速积分PID可较好地解决这一问题。
变速积分PID的基本思想是设法改变积分项的累加速度,使其与偏差大小相对应:偏差越大,积分越慢,反之则越快。变速积分PID算法为:
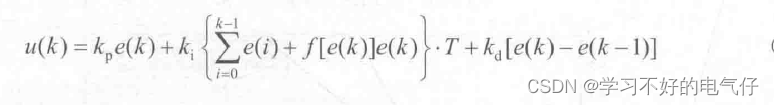
仿真实例:
设被控对象为一延迟对象:

采样时间为20s,延迟时间为4个采样时间,即 80s,取kp=0.45 ,ki=12,kd= 0.0048,A=0.4,B=0.6。取M=l,采用变速积分PID控制算法进行阶跃响应,其结果如图1和图2所示。取M=2,采用普通PID控制,其结果如图3所示。由仿真结果可以看出,变速积分与积分分离两种控制方法很类似,但调节方式不同,前者对积分项采用的是缓慢变化,而后者则采用所谓“开关”控制。变速积分调节质量更高。
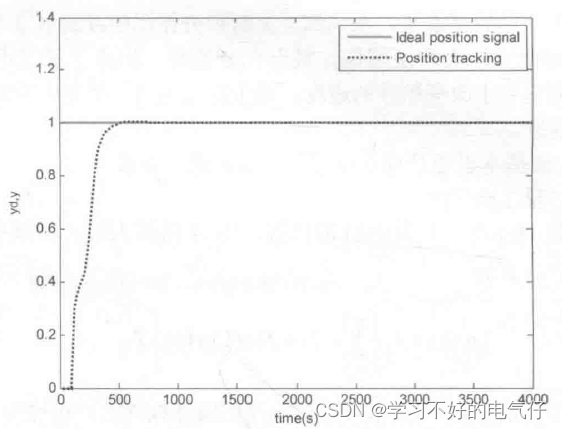
图1 变速积分阶跃响应(M=1)
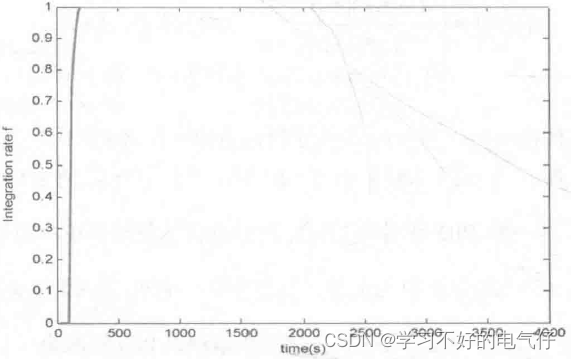
图2 变速积分参数变化
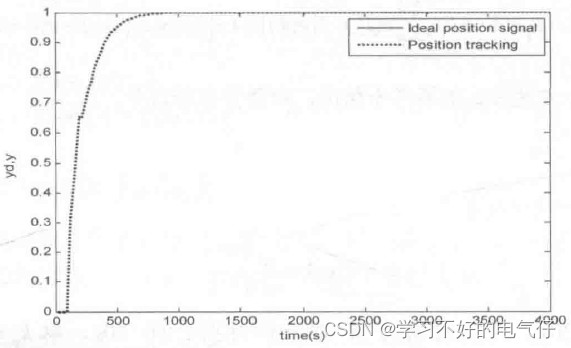
图3 普通PID控制阶跃响应(M=2)
仿真程序:
clear all;close all;
%Big time delay Plantts=20;
sys=tf([1].[60,1].'inputdelay', 80);
dsys=c2d(sys,ts,'zoh');
[num,denJ
u_1=0;u_2=0;u_3=0;u_4=0;u_5=0;
y_1=0;y_2=0;y_3=0;
error_1=0;error_2=0;
ei=0;
for k=1:1:200
time(k)k*ts;
yd(k)=1.0; %Step Signal
%Linear model
y(k)=-den(2)*y_1+num(2)*u_5;error(k)-yd(k)-y(k);
kp=0.45;kd=12;ki=0.0048;A=0.4;B=0.6;
%T type integration
ei=ei+(error(k)+error_1)/2*ts;
M=1;
if M==1 %Changing integration rate
if abs(error(k))<-B
f(k)=1;
elseif abs(error(k))>B&abs(error(k))<=A+B
(K)-(A-abs(error(k))+B)/A;
else
f(K)=0;end
else if M==2 %Not changing integration rate
f(k)=1;
end
u(k)=kp*error(k)+kd*(error(k)-error_1Yts+ki*f(k)*ei;
if u(k)>=10
u(k)=10;
end
if u(k)<=-10
u(k)-10;
end
%Return of PID parameters
u_5=u_4;u_4=u_3;u_3=u_2;u_2=u_l;u_1=u(k);y 3y_2:y_2=y_1;y_I=y(k);
error_2=error_1;
error_l=error(k);end
figure(1);
plot(time,yd,'r',time,y,'k:','linewidth',2);xlabel( 'time(s)');ylabel('ydy');
legend('Ideal position signal','Position tracking');figure(2);
plot(time,f'r,Tinewidth',2);
xlabel('time(s)');ylabel('Integration rate f);