题目描述

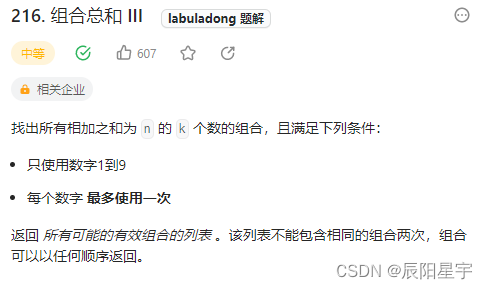
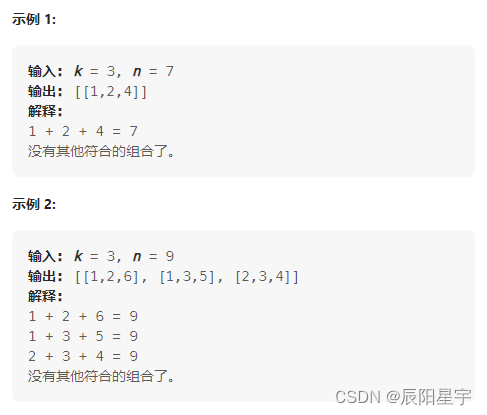
在这里插入图片描述

原题链接：216.组合总和III

解题思路

整体回溯法思路类似于 77. 组合（回溯法+剪枝优化），与之不同的是，需要多一个相加和为n的判定条件，可以让每次传入数的时候进行n - i，直至找到n == 0时，再将结果压入结果集中。

一、回溯法

class Solution {
public:
    vector<vector<int>> res;
    void backtracking(int k, int n, int startIndex, vector<int> path) {    
        if(path.size() == k) {                        
            if(n == 0) {
                res.push_back(path);                      
            }
            return ;
        }
        for(int i = startIndex; i <= 9; i++) {
            path.push_back(i);
            backtracking(k, n - i, i + 1, path);
            path.pop_back();
        }
    }
    vector<vector<int>> combinationSum3(int k, int n) {
        vector<int> path;
        backtracking(k, n, 1, path);
        return res;
    }
};

二、剪枝优化

可利用从小到大的顺序遍历、startIndex控制遍历下界、n - (k - path.size())控制遍历上界，从而实现剪枝的过程。
其中，path.size()：表示当前已存入的数，k - path.size()：表示当前还可以再存几个数，n - (k - path.size()) + 1：表示当前最大的遍历起始位置。

class Solution {
public:
    vector<vector<int>> res;
    void backtracking(int k, int n, int startIndex, vector<int> path) {    
        if(path.size() == k) {                        
            if(n == 0) {
                res.push_back(path);                      
            }
            return ;
        }
        // 当startIndex控制遍历下界，9 - (k - path.size()) + 1控制遍历上界
        for(int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) {
            path.push_back(i);
            // n - i < 0说明当前以及后面的数都不会满足要求，直接返回即可
            if(n - i < 0)      return ;
            backtracking(k, n - i, i + 1, path);
            path.pop_back();
        }
    }
    vector<vector<int>> combinationSum3(int k, int n) {
        vector<int> path;
        backtracking(k, n, 1, path);
        return res;
    }
};