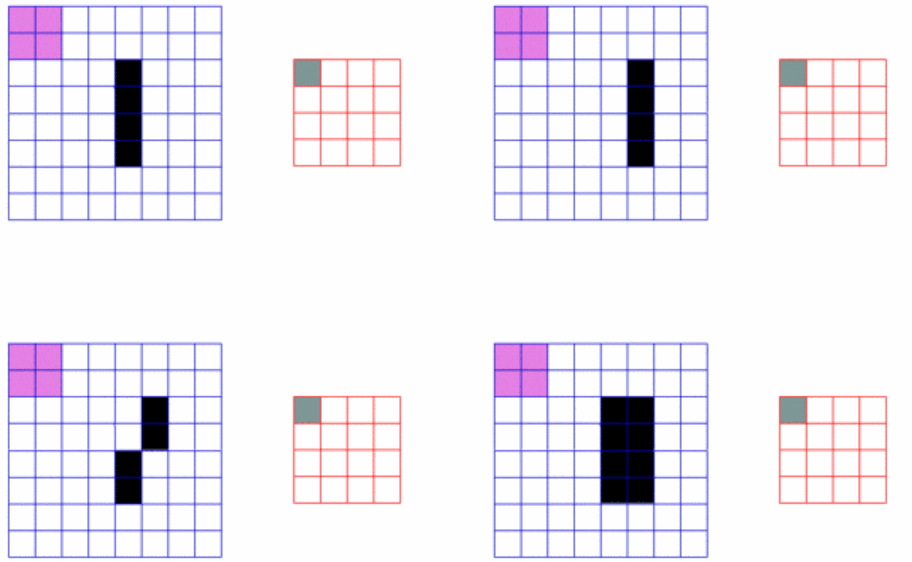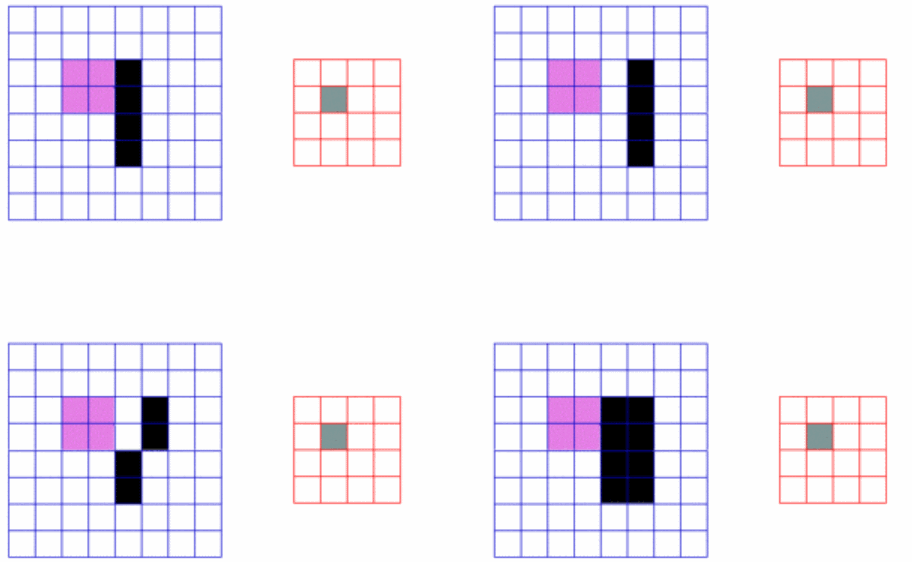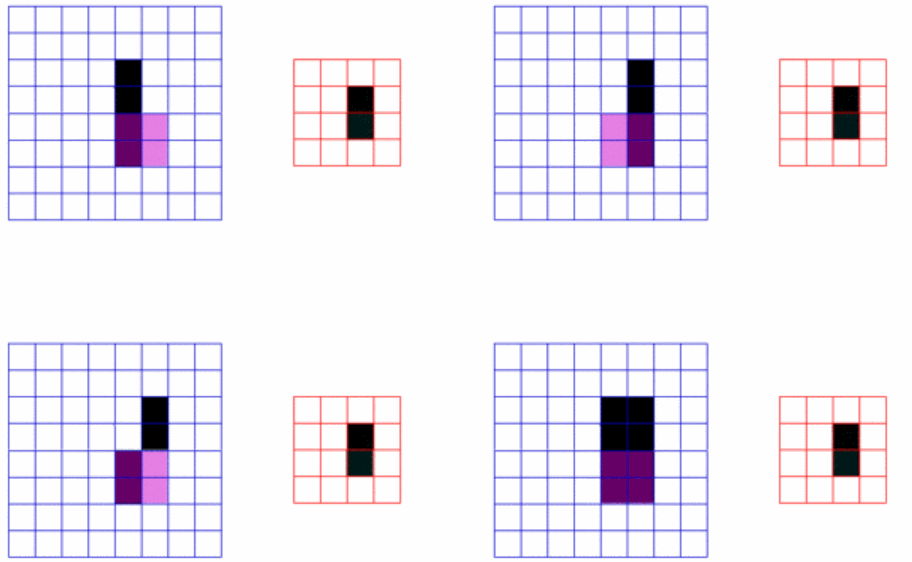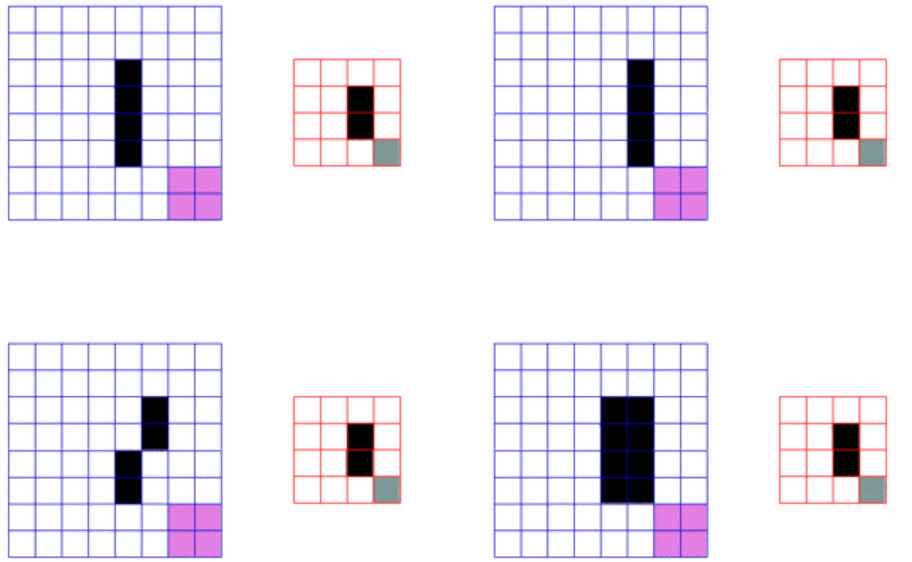
回溯思路
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}77. 组合
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2
输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]
示例 2:
输入:n = 1, k = 1
输出:[[1]]
问题分析:
1、递归函数的返回值和参数
本题参数为:n(数的范围是[1-n])、k(k个数为一组)、startIndex(记录当前层搜索开始的位置,初始为1),类型都为int。
2、回溯函数终止条件
当path.size==k时即终止,并把path路径加到result二维集合中
3、单层搜索的过程
for循环用来横向遍历,递归的过程是纵向遍历。
class Solution {
List<List<Integer>> result=new ArrayList<>();
List<Integer> path=new ArrayList<>();
public List<List<Integer>> combine(int n, int k) {
//int startIndex=1;
backtracking(n,k,1);
return result;
}
public void backtracking(int n,int k,int startIndex){
if (path.size()==k){
result.add(new ArrayList<>(path));
return;
}
for (int i=startIndex;i<=n;i++){
path.add(i);
backtracking(n,k,i+1);//不能是startIndex+1,因为始终为2
path.remove(path.size()-1);//回退
}
}
}优化:
对每一层进行剪枝操作,如图所示每一层至多n-(k-path.size())+1个
-
已经选择的元素个数:path.size();
-
所需需要的元素个数为: k - path.size();
-
列表中剩余元素(n-i) >= 所需需要的元素个数(k - path.size())
-
在集合n中至多要从该起始位置 : i <= n - (k - path.size()) + 1,开始遍历
为什么有个+1呢,因为包括起始位置,我们要是一个左闭的集合。
例如,n = 4,k = 3, 目前已经选取的元素为0(path.size为0),n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。从至多2开始搜索都是合理的,可以是组合[2, 3, 4]。
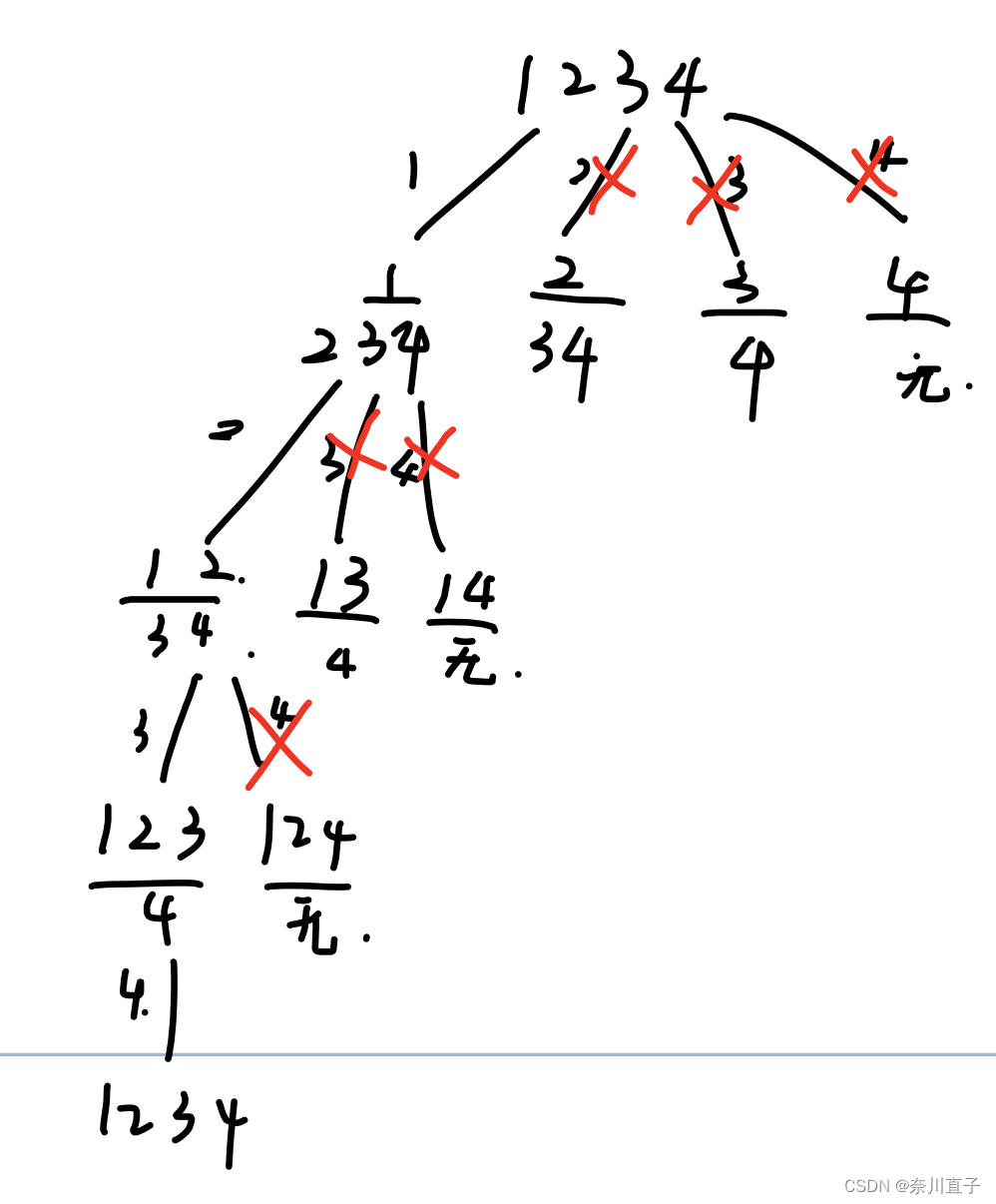
for (int i=startIndex;i<=n-(k- path.size())+1;i++){
path.add(i);
backtracking(n,k,i+1);
path.remove(path.size()-1);
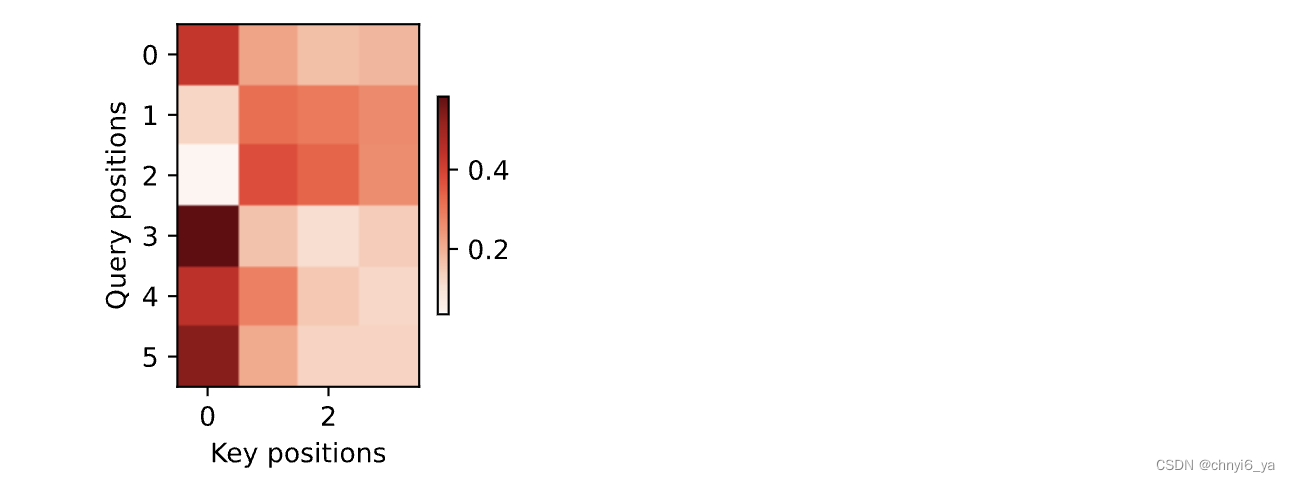
}
![[Ext JS] Grid Summary(汇总行)特性](https://img-blog.csdnimg.cn/84b3bd4a876044b38e9bb7295068504d.png)