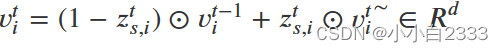【模板】树状数组 2

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1. 将某区间每一个数加上 $x$；

2. 求出某一个数的值。

输入格式

第一行包含两个整数 $N$、$M$，分别表示该数列数字的个数和操作的总个数。

第二行包含 $N$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i $ 项的初始值。

接下来 $M$ 行每行包含 $2$ 或 $4$个整数，表示一个操作，具体如下：

操作 $1$： 格式：1 x y k 含义：将区间 $[x,y]$ 内每个数加上 $k$；

操作 $2$： 格式：2 x 含义：输出第 $x$ 个数的值。

输出格式

输出包含若干行整数，即为所有操作 $2$ 的结果。

样例 #1

样例输入 #1

5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4

样例输出 #1

6
10

提示

样例 1 解释：

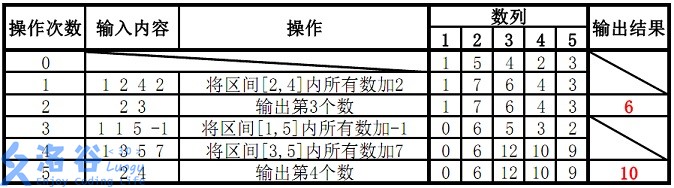
故输出结果为 6、10。

---

数据规模与约定

对于 $30\%$ 的数据：$N\le 8$，$M\le 10$；

对于 $70\%$ 的数据：$N\le 10000$，$M\le 10000$；

对于 $100\%$ 的数据：$1\le N,M\le 500000$，$1\le x,y\le n$，保证任意时刻序列中任意元素的绝对值都不大于 $2^{30}$。

#include <bits/stdc++.h>
#define LL long long 
using namespace std;
const int maxn = 1e6 + 10;
const int mod = 1e9 + 7;
const int INF = 1e9 + 10;
const int N = 1e6;
int n,m;
int a[N];
int t[N];

int lowbit(int x){
    return x&(-x);
}

int query(int x){
    int res = 0;
    while(x > 0){
        res += a[x];
        x -= lowbit(x);
    }
    return res;
}

void updata(int x,int v){
    while(x <= n){
        a[x] += v;
        x += lowbit(x); 
    } 
}

int main(){
    ios::sync_with_stdio(false); 
    cin >> n >> m;
    for(int i = 1;i <= n;i ++)
    {
        cin >> t[i];
        updata(i,t[i] - t[i - 1]);
    }
    while(m--)
    {
        int q;
        cin >> q;
        if(q == 1)
        {
            int x,y,k;
            cin >> x >> y >> k;
            updata(x,k);
            updata(y + 1,-k);
            
        }else{
            int x;
            cin >> x;
            cout << query(x) << endl;
        }
    }
    system("pause");
    return 0;
}