目录

那年深夏

引入

1.什么是深度优先搜索（DFS）？

2.什么是栈？

3.什么是递归？

图解过程

 问题示例

1、全排列问题

2、迷宫问题

3、棋盘问题（N皇后）

 4、加法分解

模板

剪枝

1.简介

2.剪枝的原则  

3.剪枝策略的寻找的方法

4.常见剪枝方法

最后

---

那年深夏

他终于抬起头，眨了眨眼睛。“停下来！”语气充满了不悦。

“啊？”

“别再丢那可恶的硬币了！”

“唔。”孙翱将硬币放回口袋，“局长先生，请您务必听我说一句。那些家伙越来越猖狂了，昨天一晚上，就……”

“说过多少次了，不要拿你们这些挖墓的事烦我”

“我们申请增加警力”，孙翱以冷静的口气问道，似乎没听见局长的话。

“另外”，孙翱站起，“他们装备比以前先进，而且似乎都想要什么同样的东西。让我不禁怀疑他们有什么后台。”说罢，还瞟了一眼局长。

局长的脸色突然变了一下，却又马上恢复。“我记得，你们那边地形很复杂。”

“当然。不过，只要有些小道具，再用深度优先搜索搜一找，几百条路线都有了”，孙翱将椅子推回桌边。

“等等”，局长猛地站起，“他们都被你们捉住了吗？”

“我让你猜猜看”，孙翱随即离去，连个招呼也不打。

对于局长的问题，他很清楚答案，是 “不”。就在昨天，就在那个雨夜，就在那个坟旁……

---

引入

1.什么是深度优先搜索（DFS）？

深度优先搜索作为初学者遇到的第一个算法，给大家留下了许多“美好”的回忆。不说废话，先来看看百度百科是怎么说的。

深度优先搜索是一种在开发爬虫早期使用较多的方法。它的目的是要达到被搜索结构的叶结点(即那些不包含任何超链的HTML文件) 。在一个HTML文件中，当一个超链被选择后，被链接的HTML文件将执行深度优先搜索，即在搜索其余的超链结果之前必须先完整地搜索单独的一条链。深度优先搜索沿着HTML文件上的超链走到不能再深入为止，然后返回到某一个HTML文件，再继续选择该HTML文件中的其他超链。当不再有其他超链可选择时，说明搜索已经结束。

TMD，笑死，根本看不懂。看看我们敬爱的jc的怎么说吧。

一种用于遍历或搜索树或图的算法。 沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都己被探寻过或者在搜寻时结点不满足条件，搜索将回溯到发现节点v的那条边的起始节点。整个进程反复进行直到所有节点都被访问为止。属于盲目搜索,最糟糕的情况算法时间复杂度为O(!n)。

来自：​​​​​​lgeneralKnowledge/基础算法/深度优先搜索.md · jimmyflower6/中山一中初中部信息竞赛 - 码云 - 开源中国 (gitee.com)

 还可以，不过，更简洁的在下面，来自《我的第一本算法书》。

深度优先搜索和广度优先搜索一样，都是对图进行搜索的算法，目的也都是从起点开始搜 索直到到达指定顶点（终点）。深度优先搜索会沿着一条路径不断往下搜索直到不能再继续为止，然后再折返，开始搜索下一条候补路径。

2.什么是栈？

定义：栈（stack）又名堆栈，它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶，相对地，把另一端称为栈底。栈是一种后进先出（last in first out）的线性表，简称LIFO。

进栈操作:向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；

出栈操作：从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。

上述材料，来自c++栈详解_Yoyo_1014的博客-CSDN博客 

​
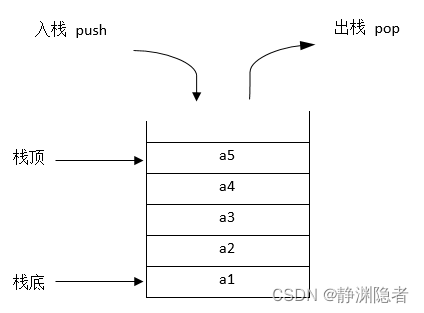
图片表示

3.什么是递归？

递归，说白了，就是函数的自身调用。通过自调用，将原问题的求解转换为许多性质相同但规模更小的子问题。

它需要满足3个条件：

1. 能够将一个问题转换成为一个新问题，并且新问题的解法和原来问题的解法类同或者相同，不同的仅是处理对象，且处理对象有一定依据。
2. 可以通过上述转化使问题一步步简化。
3. 有明确的递归出口，或者说叫递归边界。

---

图解过程

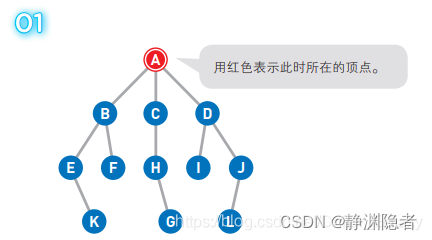
A为起点，G为终点。一开始我们在起点A上。 

将可以从A直达的三个顶点B、C、D设为下一 步的候补顶点。 

从候补顶点中选出一个 顶点。优先选择最新成为 候补的点，如果几个顶点 同时成为候补，那么可以从中随意选择一个。 

此处 B、C、D 同时成为候补，所以我们随机选择了最左边的顶点。 

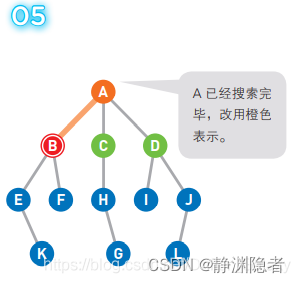
移动到选中的顶点B。此时我们在B上，所以B变为红色，同时将已经搜索过的顶点变为橙色。

此处，候补顶点是用“后入先出”（LIFO）的方式来管理的。

将可以从B直达的两个顶点E和F设为候补顶点。 

此时，最新成为候补顶点的是 E 和 F，我们选择 了左边的顶点E。 

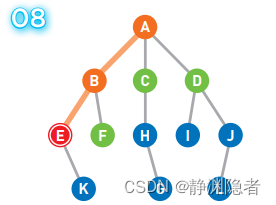
移动到选中的顶点E上。

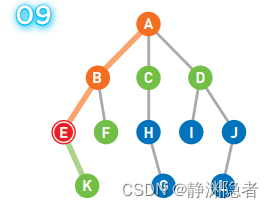
将可以从E直达的顶点K设为候补顶点。 

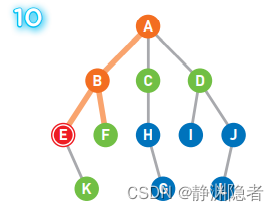
重复上述操作直到到达终点，或者所有顶点都被遍历为止。 

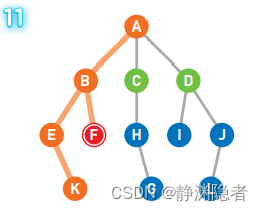
这个示例的搜索顺序为A、B、E、K、F、C、H。 

现在我们搜索到了顶点C。 

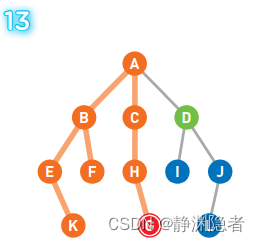
 到达终点G，搜索结束。

---

 问题示例

因为一些原因，我们将只用递归来实现深搜。

1、全排列问题

【题意】
先给一个正整数 ( 1 < = n < = 10 )，输出所有全排列。
什么是全排列，例如n＝3，输出所有组合,并且按字典序输出：
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
每个全排列一行，相邻两个数用空格隔开（最后一个数后面没有空格）
【输入格式】
一行一个整数n。
【输出格式】
输出1~n的所有全排列。
【样例输入】
3
【样例输出】
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

首先，是定义。 
定义a数组表示一排格子，它们以后用来存号码的。
定义bo数组来标记每个号码是否可填，v[i]==0表示号码i可用：可以用来填进格子。 反之不行。

然后,就是输入。
不用多说,输入n即可。

最后，就是递归部分。定义dfs(k)表示第k个数的全排列。

终止条件是k==n+1，因为到那时，前n个数都有了全排列，不用再进行加入数字了。当递归终止，输出，并用return语句返回上一层。

当未到达终止条件时，循环1-n，表示在此位置可能填上1、2、3、4、... 、n 这些数字。

当v[i]==0表示该数没被使用，就执行语句，使用。

然后就没了。

#include<bits/stdc++.h>
using namespace std;
int n;         
int a[110];    
bool v[110];   
void dfs(int k)
{
    if(k==n+1) 
    {
        for(int i=1;i<n;i++) printf("%d ",a[i]);   
        printf("%d\n",a[n]);
        return;
    }
    else
    {
        for(int i=1;i<=n;i++)
           if( v[i]==0 ) 
           {
              v[i]=1;    
              a[k]=i;    
              dfs(k+1);  
              a[k]=0;    
              v[i]=0;          
           }
    }
}
int main()
{
    scanf("%d",&n);
    memset(v,0,sizeof(v)); 
    dfs(1);                
    return 0;
}

2、迷宫问题

这类问题比较多，这里选取一道比较好的。

【题意】 
    一个n*m的网格，从出发点(stx，sty)出发到右下角(edx，edy)，只允许上下左右4个方向走到相邻的格子。
    格子为1可以走，为0无法走。输出所有可行的路线。
注意：本题没有spj，请统一用 左上右下的顺序拓展，也就是：
int dx[4]={0,-1,0,1};
int dy[4]={-1,0,1,0};
【输入格式】
    第一行是两个数n，m( 1 < n ， m < 15 ).
接下来是n行m列由1和0组成的矩阵。
最后两行是起始点和结束点。
【输出格式】
    所有可行的路径，描述一个点时用(x，y)的形式，除开始点外，其他的都要用“->”表示方向。
如果没有一条可行的路则输出-1。
【样例输入】
5 6
1 0 0 1 0 1
1 1 1 1 1 1
0 0 1 1 1 0
1 1 1 1 1 0
1 1 1 0 1 1
1 1
5 6
【样例输出】
(1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(2,5)->(3,5)->(3,4)->(3,3)->(4,3)->(4,4)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(2,5)->(3,5)->(3,4)->(4,4)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(2,5)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(3,4)->(3,3)->(4,3)->(4,4)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(3,4)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(3,4)->(4,4)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(3,4)->(2,4)->(2,5)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(3,4)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(3,4)->(4,4)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(4,3)->(4,4)->(3,4)->(2,4)->(2,5)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(4,3)->(4,4)->(3,4)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(4,3)->(4,4)->(4,5)->(5,5)->(5,6)

思路：很简单，以上下左右 四个方向进行搜索，并记录下步骤即可。重点在于输出，要细心。不过，有一个易错点需要提醒一下：在开始前，要将起点标记为已走过，不然可能出现来回横跳的情况。

#include<bits/stdc++.h>
using namespace std;
bool flag=false;
struct node{
    int x,y;
}en,st,m1[1005];
int dx[4]={0,-1,0,1};
int dy[4]={-1,0,1,0};
int n,m,a[1005][1005];
void dfs(int x,int y,int k)
{
    if(x==en.x&&y==en.y)
    {
        flag=true;
        for(int i=1;i<k;i++) printf("(%d,%d)->",m1[i].x,m1[i].y);
        printf("(%d,%d)\n",m1[k].x,m1[k].y);
        return;
    }
    for(int i=0;i<4;i++)
    {
        node nxy;
        nxy.x=dx[i]+x;
        nxy.y=dy[i]+y;
        if(a[nxy.x][nxy.y]!=0)
        {
            a[nxy.x][nxy.y]=0;
            m1[k+1]=nxy;
            dfs(nxy.x,nxy.y,k+1);
            a[nxy.x][nxy.y]=1;
        }
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            scanf("%d",&a[i][j]);
        }
    }
    scanf("%d%d%d%d",&st.x,&st.y,&en.x,&en.y);
    m1[1]=st;
    a[st.x][st.y] = 0;
    dfs(st.x,st.y,1);
    if(flag==false) printf("-1");
}

3、棋盘问题（N皇后）

【题意】
会下国际象棋的人都很清楚：皇后可以在横、竖、斜线上不限步数地吃掉其他棋子。如何将8个皇后放在棋盘上（有8 * 8个方格），使它们谁也不能被吃掉！
这就是著名的八皇后问题。
【输入格式】
一个整数n（ 1 < = n < = 10 )
【输出格式】
每行输出对应一种方案，按字典序输出所有方案。每种方案顺序输出皇后所在的列号，相邻两数之间用空格隔开。
【样例输入】
4
【样例输出】
2 4 1 3
3 1 4 2
 

思路：一行行地搜，在每一行中，循环遍历每列，用四个数组判断是否能放。（row表示行,col表示列,LL左对角线,RR表示有对角线）。对于对角线与行列的关系，是一个数学问题。这里就不详细讲解了。

#include<bits/stdc++.h>
using namespace std;
int n,a[35][35];
bool row[30],col[30],LL[30],RR[30];
void dfs(int x)
{
    if(x==n+1)
    {
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=n;j++)
            {
                if(a[i][j]==1)
                {
                    printf("%d ",j);
                }
            }
        }
        printf("\n");
    }
    else
    {
        int i=x;
        for(int j=1;j<=n;j++)
        {
            if(row[i]==0&&col[j]==0&&LL[i-j+n]==0&&RR[i+j]==0)
            {
                a[i][j]=1;
                row[i]=col[j]=LL[i-j+n]=RR[i+j]=1;
                dfs(x+1);
                a[i][j]=0;
                row[i]=col[j]=LL[i-j+n]=RR[i+j]=0;
            }
        }
    }
}
int main()
{
    scanf("%d",&n);
    memset(row,0,sizeof(row));
    memset(col,0,sizeof(col));
    memset(LL,0,sizeof(LL));
    memset(RR,0,sizeof(RR));
    memset(a,0,sizeof(a));
    dfs(1);
    return 0;
}

 4、加法分解

【题意】（本题附有视频）
    输入自然数n，然后将其分拆成由若干数相加的形式，参与加法运算的数可以重复。具体格式请仔细研究样例输出！
【输入格式】
    待拆分的自然数n(n<=50)。
【输出格式】
    若干数的加法式子。
【输入样例】
7
【输出样例】
1+6
1+1+5
1+1+1+4
1+1+1+1+3
1+1+1+1+1+2
1+1+1+1+1+1+1
1+1+1+2+2
1+1+2+3
1+2+4
1+2+2+2
1+3+3
2+5
2+2+3
3+4
 

思路日后更新。。。

#include<bits/stdc++.h>
using namespace std;
int n,a[55];
void dfs(int x,int k)
{
    if(k>1)
    {
        for(int i=1;i<k;i++) printf("%d+",a[i]);
        printf("%d\n",x);
    }
    for(int i=a[k-1];i<=x/2;i++)
    {
        a[k]=i;
        dfs(x-i,k+1);
        a[k]=0;
    }   
}
int main()
{
    scanf("%d",&n);
    a[0]=1;
    dfs(n,1);
}

---

模板

虽然不那么明显，但深搜也是有一套模板的。

void dfs(int step)
 
{
 
    判断边界
 
    {
 
        相应操作
 
        }
 
    尝试每一种可能
 
    {
 
        满足check条件
 
        标记
 
        继续下一步dfs(step+1)
 
        恢复初始状态（回溯的时候要用到）
 
    }
 
}

---

剪枝

        剪枝，就是减小搜索树规模、尽早排除搜索树中不必要的分支的一种手段。形象地看，就好像剪掉了搜索树的枝条，故被称为剪枝。

1.简介

    在搜索算法中优化中，剪枝，就是通过某种判断，避免一些不必要的遍历过程，形象的说，就是剪去了搜索树中的某些“枝条”，故称剪枝。应用剪枝优化的核心问题是设计剪枝判断方法，即确定哪些枝条应当舍弃，哪些枝条应当保留的方法。

2.剪枝的原则  

1） 正确性

  正如上文所述,枝条不是爱剪就能剪的. 如果随便剪枝,把带有最优解的那一分支也剪掉了的话,剪枝也就失去了意义. 所以,剪枝的前提是一定要保证不丢失正确的结果.

  2）准确性

  在保证了正确性的基础上,我们应该根据具体问题具体分析,采用合适的判断手段,使不包含最优解的枝条尽可能多的被剪去,以达到程序“最优化”的目的. 可以说,剪枝的准确性,是衡量一个优化算法好坏的标准.

 3）高效性

设计优化程序的根本目的,是要减少搜索的次数,使程序运行的时间减少. 但为了使搜索次数尽可能的减少,我们又必须花工夫设计出一个准确性较高的优化算法,而当算法的准确性升高,其判断的次数必定增多,从而又导致耗时的增多,这便引出了矛盾. 因此,如何在优化与效率之间寻找一个平衡点,使得程序的时间复杂度尽可能降低,同样是非常重要的. 倘若一个剪枝的判断效果非常好,但是它却需要耗费大量的时间来判断、比较,结果整个程序运行起来也跟没有优化过的没什么区别,这样就太得不偿失了.

3.剪枝策略的寻找的方法

1）微观方法：从问题本身出发，发现剪枝条件

2）宏观方法：从整体出发，发现剪枝条件。

3）注意提高效率，这是关键，最重要的。

总之，剪枝策略，属于算法优化范畴；通常应用在DFS 和 BFS 搜索算法中；剪枝策略就是寻找过滤条件，提前减少不必要的搜索路径。

4.常见剪枝方法

a.优化搜索顺序
在一些问题中，搜索树的各个分支之间的顺序是不固定的不同的搜索顺序会产生不同的搜索形态，规模也相差甚远

b.排除等效分支

在搜索过程中，如果我们能够得知搜索树的当前节点沿着某几条不同分支到达的子树是等效的，那么只需要对其中一条路径进行搜索

c.是否可行剪枝

在搜索过程中，每次对当前状态进行检查，如果发现不可能到达递归边界，就执行回溯

d.最优性剪枝

在求解最优解的过程中，如果当前解已经没有当前最优解优秀，此时可以执行回溯语句

e.记忆化剪枝

记录每个状态的搜索结果，在重复遍历一个状态时返回。

参考资料：剪枝算法_命z的博客-CSDN博客_剪枝算法

---

最后

再见，给个点赞吧！